Theodorus of Cyrene
Encyclopedia
Theodorus of Cyrene
was a Greek
mathematician
of the 5th century BC. The only first-hand accounts of him that we have are in two of Plato
's dialogues: the Theaetetus
and the Sophist
. In the former, his student Theaetetus
attributes to him the theorem that the square roots of the non-square numbers up to 17 are irrational:
(The square containing two square units is not mentioned, perhaps because the incommensurability of its side with the unit was already known.)
Theodorus's method of proof is not known. It is not even known whether, in the quoted passage,
"up to" (μέχρι) means that seventeen is included. If seventeen is excluded, then Theodorus's proof may have relied merely on considering whether numbers are even or odd. Indeed, Hardy and Wright
and Knorr suggest proofs that rely ultimately on the following theorem: If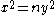
is soluble in integers, and 
is odd, then 
must be congruent
to 1 modulo 8 (since
and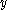 
can be assumed odd, so their squares are congruent to 1 modulo 8).
A possibility suggested earlier by Zeuthen
is that Theodorus applied the so-called Euclidean algorithm
, formulated in Proposition X.2 of the Elements
as a test for incommensurability. In modern terms, the theorem is that a real number with an infinite continued fraction
expansion is irrational. Irrational square roots have periodic expansions. The period of the square root of 19 has length 6, which is greater than the period of the square root of any smaller number. The period of √17 has length one (so does √18; but the irrationality of √18 follows from that of √2).
The so-called Spiral of Theodorus
is composed of contiguous right triangle
s with hypotenuse
lengths equal √2, √3, √4, …, √17; additional triangles cause the diagram to overlap.
Philip J. Davis
interpolated
the vertices of the spiral to get a continuous curve. He discusses the history of attempts to determine Theodorus' method in his book Spirals: From Theodorus to Chaos, and makes brief references to the matter in his fictional Thomas Gray series.
That Theaetetus established a more general theory of irrationals,
whereby square roots of non-square numbers are irrational, is suggested in the eponymous Platonic dialogue as well as commentary on, and scholia to, the Elements.
Cyrene, Libya
Cyrene was an ancient Greek colony and then a Roman city in present-day Shahhat, Libya, the oldest and most important of the five Greek cities in the region. It gave eastern Libya the classical name Cyrenaica that it has retained to modern times.Cyrene lies in a lush valley in the Jebel Akhdar...
was a Greek
Ancient Greece
Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
of the 5th century BC. The only first-hand accounts of him that we have are in two of Plato
Plato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
's dialogues: the Theaetetus
Theaetetus (dialogue)
The Theaetetus is one of Plato's dialogues concerning the nature of knowledge. The framing of the dialogue begins when Euclides tells his friend Terpsion that he had written a book many years ago based on what Socrates had told him of a conversation he'd had with Theaetetus when Theaetetus was...
and the Sophist
Sophist (dialogue)
The Sophist is a Platonic dialogue from the philosopher's late period, most likely written in 360 BCE. Having criticized his Theory of Forms in the Parmenides, Plato presents a new conception of the forms in the Sophist, more mundane and down-to-earth than its predecessor...
. In the former, his student Theaetetus
Theaetetus
Theaetetus could mean:* Theaetetus , a Greek geometer* Theaetetus , a dialogue by Plato, named after the geometer* Theaetetus , a lunar impact crater....
attributes to him the theorem that the square roots of the non-square numbers up to 17 are irrational:
Theodorus here was drawing some figures for us in illustration of roots, showing that squares containing three square feet and five square feet are not commensurable in length with the unit of the foot, and so, selecting each one in its turn up to the square containing seventeen square feet and at that he stopped.
(The square containing two square units is not mentioned, perhaps because the incommensurability of its side with the unit was already known.)
Theodorus's method of proof is not known. It is not even known whether, in the quoted passage,
"up to" (μέχρι) means that seventeen is included. If seventeen is excluded, then Theodorus's proof may have relied merely on considering whether numbers are even or odd. Indeed, Hardy and Wright
and Knorr suggest proofs that rely ultimately on the following theorem: If
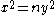is soluble in integers, and is odd, then must be congruentModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
to 1 modulo 8 (since
and 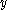can be assumed odd, so their squares are congruent to 1 modulo 8).A possibility suggested earlier by Zeuthen
Hieronymus Georg Zeuthen
Hieronymus Georg Zeuthen was a Danish mathematician.He is known for work on the enumerative geometry of conic sections, algebraic surfaces, and history of mathematics.-Biography:...
is that Theodorus applied the so-called Euclidean algorithm
Euclidean algorithm
In mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
, formulated in Proposition X.2 of the Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
as a test for incommensurability. In modern terms, the theorem is that a real number with an infinite continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
expansion is irrational. Irrational square roots have periodic expansions. The period of the square root of 19 has length 6, which is greater than the period of the square root of any smaller number. The period of √17 has length one (so does √18; but the irrationality of √18 follows from that of √2).
The so-called Spiral of Theodorus
Spiral of Theodorus
In geometry, the spiral of Theodorus is a spiral composed of contiguous right triangles. It was first constructed by Theodorus of Cyrene.-Construction:...
is composed of contiguous right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
s with hypotenuse
Hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
lengths equal √2, √3, √4, …, √17; additional triangles cause the diagram to overlap.
Philip J. Davis
Philip J. Davis
Philip J. Davis is an American applied mathematician.Davis was born in Lawrence, Massachusetts. He is known for his work in numerical analysis and approximation theory, as well as his investigations in the history and philosophy of mathematics...
interpolated
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
the vertices of the spiral to get a continuous curve. He discusses the history of attempts to determine Theodorus' method in his book Spirals: From Theodorus to Chaos, and makes brief references to the matter in his fictional Thomas Gray series.
That Theaetetus established a more general theory of irrationals,
whereby square roots of non-square numbers are irrational, is suggested in the eponymous Platonic dialogue as well as commentary on, and scholia to, the Elements.
See also
- Cyrene, LibyaCyrene, LibyaCyrene was an ancient Greek colony and then a Roman city in present-day Shahhat, Libya, the oldest and most important of the five Greek cities in the region. It gave eastern Libya the classical name Cyrenaica that it has retained to modern times.Cyrene lies in a lush valley in the Jebel Akhdar...
- Chronology of ancient Greek mathematicians
- Quadratic irrationalQuadratic irrationalIn mathematics, a quadratic irrational is an irrational number that is the solution to some quadratic equation with rational coefficients...
- Wilbur KnorrWilbur KnorrWilbur Richard Knorr was an American historian of mathematics and a professor in the departments of philosophy and classics at Stanford University. He has been called "one of the most profound and certainly the most provocative historian of Greek mathematics" of the 20th century.-Biography:Knorr...