Spiral of Theodorus
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
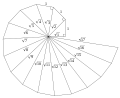
, the spiral of Theodorus (also called square root spiral, Einstein spiral or Pythagorean spiral) is a spiral
Spiral
In mathematics, a spiral is a curve which emanates from a central point, getting progressively farther away as it revolves around the point.-Spiral or helix:...
composed of contiguous right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
s. It was first constructed by Theodorus of Cyrene
Theodorus of Cyrene
Theodorus of Cyrene was a Greek mathematician of the 5th century BC. The only first-hand accounts of him that we have are in two of Plato's dialogues: the Theaetetus and the Sophist...
.
Construction
The spiral is started with an isosceles right triangle, with each legCathetus
In a right triangle, the cathetus , commonly known as a leg, is either of the sides that are adjacent to the right angle. It is occasionally called the periphrasis . The side opposite the right angle is the hypotenuse...
having a length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
of 1. Another right triangle is formed, an automedian right triangle
Automedian triangle
In plane geometry, an automedian triangle is a triangle in which the lengths of the three medians are proportional to the lengths of the three sides, in a different order...
with one leg being the hypotenuse
Hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
of the prior triangle (with length √2
Square root of 2
The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
) and the other leg having length of 1; the length of the hypotenuse of this second triangle is √3
Square root of 3
The square root of 3 is the positive real number that, when multiplied by itself, gives the number 3. It is more precisely called the principal square root of 3, to distinguish it from the negative number with the same property...
. The process then repeats; the ith triangle in the sequence is a right triangle with side lengths √i and 1, and with hypotenuse √(i + 1).
History
Although all of Theodorus' work has been lost, PlatoPlato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
put Theodorus into his dialogue Theaetetus
Theaetetus (dialogue)
The Theaetetus is one of Plato's dialogues concerning the nature of knowledge. The framing of the dialogue begins when Euclides tells his friend Terpsion that he had written a book many years ago based on what Socrates had told him of a conversation he'd had with Theaetetus when Theaetetus was...
, which tells the reader of his achievements. It is assumed that Theodorus had proved that all of the square roots of non-square integers from 3 to 17 are irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
by means of the Spiral of Theodorus.
Plato quoted Theaetetus
Theaetetus (mathematician)
Theaetetus, Theaitētos, of Athens, possibly son of Euphronius, of the Athenian deme Sunium, was a classical Greek mathematician...
speaking to Socrates
Socrates
Socrates was a classical Greek Athenian philosopher. Credited as one of the founders of Western philosophy, he is an enigmatic figure known chiefly through the accounts of later classical writers, especially the writings of his students Plato and Xenophon, and the plays of his contemporary ...
:
It was about the nature of roots. Theodorus was describing them to us and showing that the third root and the fifth root, represented by the sides of squares, had no common measure. He took them up one by one until he reached the seventeenth, when he stopped. It occurred to us, since the number of roots appeared to be infinite, to try to bring them all under one denomination.
Plato does not attribute the irrationality of the square root of 2
Square root of 2
The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
to Theodorus, because it was well known before him. Theodorus and Theaetetus split the rational numbers and irrational numbers into different categories.
Hypotenuse
Each of the triangle's hypotenuse hi gives the square rootSquare root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
to a consecutive natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
, with h1 = √2
Plato, tutored by Theodorus, questioned why Theodorus stopped at √17. The reason is commonly believed to be that the √17 hypotenuse belongs to the last triangle that does not overlap the figure.
Overlapping
In 1958, E. Teuffel proved that no two hypotenuses will ever coincide, regardless of how far the spiral is continued. Also, if the sides of unit "one" length are extended into a lineLine (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
, they will never pass through any of the other vertices of the total figure.
Extension
Angle
If φn is the angle of the nth triangle (or spiral segment), then: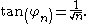
Therefore, the growth of the angle φn of the next triangle n is:
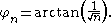
The sum of the angles of the first k triangles is called the total angle φ(k) for the kth triangle, and it equals:
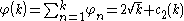
with
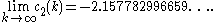
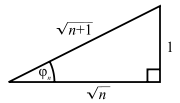
Radius
The growth of the radius of the spiral at a certain triangle n is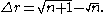
Archimedean spiral
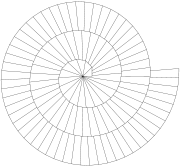
The Spiral of Theodorus approximates the Archimedean spiralArchimedean spiral
The Archimedean spiral is a spiral named after the 3rd century BC Greek mathematician Archimedes. It is the locus of points corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity...
. Just as the distance between two windings of the Archimedean spiral equals mathematical constant
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
pi
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, as the number of spins of the spiral of Theodorus approaches infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
, the distance between two consecutive windings quickly approaches π.
The following is a table showing the distance of two windings of the spiral approaching pi:
| Winding No.: | Calculated average winding-distance | Accuracy of average winding-distance in comparison to π |
|---|---|---|
| 2 | 3.1592037 | 99.44255% |
| 3 | 3.1443455 | 99.91245% |
| 4 | 3.14428 | 99.91453% |
| 5 | 3.142395 | 99.97447% |
| → ∞ | → π | → 100% |
As shown, after only the fifth winding, the distance is a 99.97% accurate approximation to π.
Continuous curve
The question of how to interpolateInterpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
the discrete points of the spiral of Theodorus by a smooth curve (not merely piecewise continuous), similar to the way in which the Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
interpolates the factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
function, was proposed and answered in by analogy with Euler's formula for the gamma function. He found the function:
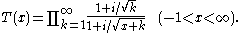
An axiomatic characterization of this function is given in as the unique function that satisfies the functional equation
Functional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
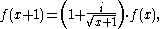
the initial condition
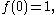and monotonicity in both argument and modulus; alternative conditions and weakenings are also studied therein.An alternative derivation is given in .
Some suggested an alternative interpolation which connects the spiral and an alternative inner spiral, as in .