Topological data analysis
Encyclopedia
Topological data analysis is a new area of study aimed at having applications in areas such as data mining
and computer vision
.
The main problems are:
The human brain can easily extract global structure from representations in a strictly lower dimension, i.e. we infer a 3D environment from a 2D image from each eye. The inference of global structure also occurs when converting discrete data into continuous images, e.g. dot-matrix printers and televisions communicate images via arrays of discrete points.
The main method used by topological data analysis is:
En. The global shape of the data may provide information about the phenomena that the data represent.
One type of data set for which global features are certainly present is the so-called point cloud data coming from physical objects in 3D. E.g. a laser can scan an object at a set of discrete points and the cloud of such points can be used in a computer representation of the object. Point cloud data refers to any collection of points in En or a (perhaps noisy) sample of points on a lower-dimensional subset.
For point clouds in low-dimensional spaces there are numerous approaches for inferring features based on planar projections in the fields of computer graphics
and statistics
. Topological data analysis is needed when the spaces are high-dimensional or too twisted to allow planar projections.
To convert a point cloud in a metric space
into a global object, use the point cloud as the
vertices of a graph
whose edges are determined by proximity, then turn the graph into a simplicial complex
and use algebraic topology to study it. An alternative approach is the minimum spanning tree-based method in the geometric data clustering. If a group of data points forms a cluster, then the geometry of this point cloud can be determined.
for an introduction to the notation.
Persistent homology essentially calculates homology groups at different resolutions to see which features persist for long periods of time. It is assumed that important features and structures are the ones that persist. We define persistent homology as follows:
Let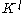
be a filtration. The p-persistent kth homology group of 
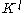is 
.
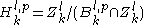If we let
be a nonbounding 
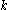-cycle created at time 
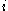by simplex 
and let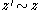 
be a homologous 
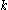-cycle that becomes a boundary cycle at time 
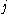by simplex 
, then we can define the persistence of 
as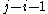 
. We call 
the creator of 
and 
the destroyer of 
. If 
does not have a destroyer, its persistence is 
.
Instead of using an index-based filtration, we can use a time-based filtration. Let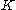
be a simplicial complex
and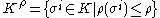
be a filtration defined for an associated map 
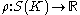that maps simplices in the final complex to real numbers. Then for all real numbers 
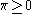, the 
-persistent kth homology group of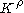 
is 
. The persistence of a 
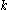-cycle created at time 
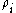and destroyed at 
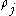is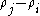 
.
Data mining
Data mining , a relatively young and interdisciplinary field of computer science is the process of discovering new patterns from large data sets involving methods at the intersection of artificial intelligence, machine learning, statistics and database systems...
and computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
.
The main problems are:
- how one infers high-dimensional structure from low-dimensional representations; and
- how one assembles discrete points into global structure.
The human brain can easily extract global structure from representations in a strictly lower dimension, i.e. we infer a 3D environment from a 2D image from each eye. The inference of global structure also occurs when converting discrete data into continuous images, e.g. dot-matrix printers and televisions communicate images via arrays of discrete points.
The main method used by topological data analysis is:
- Replace a set of data points with a family of simplicial complexSimplicial complexIn mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
es, indexed by a proximity parameter. - Analyse these topological complexes via algebraic topologyAlgebraic topologyAlgebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
— specifically, via the new theory of persistent homology. - Encode the persistent homology of a data set in the form of a parameterized version of a Betti numberBetti numberIn algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
which will be called a barcode.
Point cloud data
Data is often represented as points in a Euclidean n-dimensional spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
En. The global shape of the data may provide information about the phenomena that the data represent.
One type of data set for which global features are certainly present is the so-called point cloud data coming from physical objects in 3D. E.g. a laser can scan an object at a set of discrete points and the cloud of such points can be used in a computer representation of the object. Point cloud data refers to any collection of points in En or a (perhaps noisy) sample of points on a lower-dimensional subset.
For point clouds in low-dimensional spaces there are numerous approaches for inferring features based on planar projections in the fields of computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
. Topological data analysis is needed when the spaces are high-dimensional or too twisted to allow planar projections.
To convert a point cloud in a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
into a global object, use the point cloud as the
vertices of a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
whose edges are determined by proximity, then turn the graph into a simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
and use algebraic topology to study it. An alternative approach is the minimum spanning tree-based method in the geometric data clustering. If a group of data points forms a cluster, then the geometry of this point cloud can be determined.
Persistent homology
See homologyHomology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
for an introduction to the notation.
Persistent homology essentially calculates homology groups at different resolutions to see which features persist for long periods of time. It is assumed that important features and structures are the ones that persist. We define persistent homology as follows:
Let
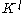be a filtration. The p-persistent kth homology group of 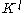is 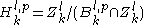.If we let
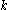be a nonbounding -cycle created at time 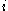by simplex and let 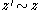be a homologous 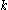-cycle that becomes a boundary cycle at time 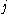by simplex , then we can define the persistence of as 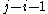. We call the creator of and the destroyer of . If does not have a destroyer, its persistence is .Instead of using an index-based filtration, we can use a time-based filtration. Let
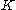be a simplicial complexSimplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
and
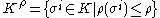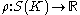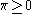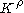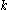be a filtration defined for an associated map that maps simplices in the final complex to real numbers. Then for all real numbers , the -persistent kth homology group of is . The persistence of a -cycle created at time 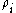and destroyed at 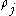is 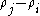.See also
- Dimensionality reductionDimensionality reductionIn machine learning, dimension reduction is the process of reducing the number of random variables under consideration, and can be divided into feature selection and feature extraction.-Feature selection:...
- Data miningData miningData mining , a relatively young and interdisciplinary field of computer science is the process of discovering new patterns from large data sets involving methods at the intersection of artificial intelligence, machine learning, statistics and database systems...
- Computer visionComputer visionComputer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
- Computational topology
- Digital topologyDigital topologyDigital topology deals with properties and features of two-dimensional or three-dimensional digital imagesthat correspond to topological properties or topological features of objects....
- Digital Morse theoryDigital Morse theoryIn mathematics, digital Morse theory is a digital adaptation of continuum Morse theory for scalar volume data.The main utility of a digital Morse theory is that it serves to provide a theoretical basis for isosurfaces, and perpendicular streamlines....
- Shape analysisShape analysisThis article describes shape analysis to analyze and process geometric shapes.The shape analysis described here is related to the statistical analysis of geometric shapes, to shape matching and shape recognition...
- Size theory
- Structured data analysis (statistics)Structured data analysis (statistics)Structured data analysis is the statistical data analysis of structured data. This can arise either in the form of an a priori structure such as multiple-choice questionnaires or in situations with the need to search for structure that fits the given data, either exactly or approximately...
Further reading
- Topological Methods in Scientific Computing, Statistics and Computer Science Stanford group
- BARCODES: THE PERSISTENT TOPOLOGY OF DATA
- Topological Data Analysis: the algebraic topology of point data clouds?
- TOPOLOGY AND DATA, GUNNAR CARLSSON, BULLETIN (New Series) OF THE AMERICAN MATHEMATICAL SOCIETY, Volume 46, Number 2, April 2009, Pages 255–308, Article electronically published on January 29, 2009
- Computational Topology: An Introduction, Herbert Edelsbrunner, John L. Harer, AMS Bookstore, 2010, ISBN 9780821849255
- Topological Methods in Data Analysis and Visualization: Theory, Algorithms, and Applications, Editors Valerio Pascucci, Hans Hagen, Xavier Tricoche, Julien Tierny, Springer, 2010, ISBN 9783642150135.