The transfer-matrix method is a method used in optics

Optics

Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...

 and acoustics

Acoustics

Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...

 to analyze the propagation of electromagnetic or acoustic wave

Acoustic wave

Acoustic waves are a type of longitudinal waves that propagate by means of adiabatic compression and decompression. Longitudinal waves are waves that have the same direction of vibration as their direction of travel. Important quantities for describing acoustic waves are sound pressure, particle...

s through a stratified (layered) medium. This is for example relevant for the design of anti-reflective coating

Anti-reflective coating

An antireflective or anti-reflection coating is a type of optical coating applied to the surface of lenses and other optical devices to reduce reflection. This improves the efficiency of the system since less light is lost. In complex systems such as a telescope, the reduction in reflections also...

s and dielectric mirror

Dielectric mirror

A dielectric mirror is a type of a mirror composed of multiple thin layers of dielectric material, typically deposited on a substrate of glass or some other optical material. By careful choice of the type and thickness of the dielectric layers, one can design an optical coating with specified...

s.

The reflection

Reflection (physics)

Reflection is the change in direction of a wavefront at an interface between two differentmedia so that the wavefront returns into the medium from which it originated. Common examples include the reflection of light, sound and water waves...

 of light

Light

Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...

 from a single interface between two media

Medium (optics)

An optical medium is material through which electromagnetic waves propagate. It is a form of transmission medium. The permittivity and permeability of the medium define how electromagnetic waves propagate in it...

 is described by the Fresnel equations

Fresnel equations

The Fresnel equations , deduced by Augustin-Jean Fresnel , describe the behaviour of light when moving between media of differing refractive indices...

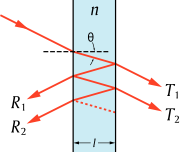
. However, when there are multiple interfaces, such as in the figure, the reflections themselves are also partially transmitted and then partially reflected. Depending on the exact path length, these reflections can interfere destructively or constructively. The overall reflection of a layer structure is the sum of an infinite number of reflections, which is cumbersome to calculate.

The transfer-matrix method is based on the fact that, according to Maxwell's equations

Maxwell's equations

Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...

, there are simple continuity conditions for the electric field

Electric field

In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...

 across boundaries from one medium to the next. If the field is known at the beginning of a layer, the field at the end of the layer can be derived from a simple matrix

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

 operation. A stack of layers can then be represented as a system matrix, which is the product of the individual layer matrices. The final step of the method involves converting the system matrix back into reflection and transmission coefficient

Transmission coefficient

The transmission coefficient is used in physics and electrical engineering when wave propagation in a medium containing discontinuities is considered...

s.

Formalism for electromagnetic waves

Below is described how the transfer matrix is applied to electromagnetic waves (for example light) of a given frequency

Frequency

Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...

 propagating through a stack of layers at normal incidence

Surface normal

A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...

. It can be generalized to deal with incidence at an angle, absorbing media

Absorption (electromagnetic radiation)

In physics, absorption of electromagnetic radiation is the way by which the energy of a photon is taken up by matter, typically the electrons of an atom. Thus, the electromagnetic energy is transformed to other forms of energy for example, to heat. The absorption of light during wave propagation is...

, and media with magnetic properties

Permeability (electromagnetism)

In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it is the degree of magnetization that a material obtains in response to an applied magnetic field. Magnetic permeability is typically...

. We assume that the stack layers are normal to the axis and that the field within one layer can be represented as the superposition of a left- and right-traveling wave with wave number ,.
Because it follows from Maxwell's equation that and must be continuous across a boundary, it is convenient to represent the field as the vector , where.
Since there are two equations relating and to and , these two representations are equivalent. In the new representation, propagation over a distance into the positive direction is described by the matrix
and
Such a matrix can represent propagation through a layer if is the wave number in the medium and the thickness of the layer:
For a system with layers, each layer has a transfer matrix , where increases towards higher values. The system transfer matrix is then

Typically, one would like to know the reflectance and transmittance

Transmittance

In optics and spectroscopy, transmittance is the fraction of incident light at a specified wavelength that passes through a sample. A related term is absorptance, or absorption factor, which is the fraction of radiation absorbed by a sample at a specified wavelength...

 of the layer structure. If the layer stack starts at , then for negative , the field is described as,
where is the amplitude of the incoming wave, the wave number in the left medium, and is the amplitude (not intensity!) reflectance coefficient of the layer structure. On the other side of the layer structure, the field consists of a right-propagating transmitted field,
where is the amplitude transmittance and is the wave number in the rightmost medium. If and , then we can solve
in terms of the matrix elements of the system matrix and obtain


and
.

The transmittance and reflectance (i.e., the fractions of the incident intensity transmitted and reflected by the layer) are often of more practical use and are given by and , respectively.

Example

As an illustration, consider a single layer of glass with a refractive index n and thickness d suspended in air at a wave number k (in air). In glass, the wave number is . The transfer matrix is.
The amplitude reflection coefficient can be simplified to.
This configuration effectively describes a Fabry–Pérot interferometer or etalon: for , the reflection vanishes.

Acoustic waves

It is possible to apply the transfer-matrix method to sound waves. Instead of the electric field E and its derivative F, the displacement u and the stress

Stress (physics)

In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...

 , where is the p-wave modulus

P-wave modulus

In linear elasticity, the P-wave modulus M, also known as the longitudinal modulus, is one of the elastic moduli available to describe isotropic homogeneous materials....

, should be used.

Abeles matrix formalism

The Abeles matrix method is a computationally fast and easy way to calculate the specular reflectivity from a stratified interface, as a function of the perpendicular momentum transfer, Q_z.

Application

Where θ is the angle of incidence/reflection of the incident radiation

Radiation

In physics, radiation is a process in which energetic particles or energetic waves travel through a medium or space. There are two distinct types of radiation; ionizing and non-ionizing...

 and λ is the wavelength of the radiation.
The measured reflectivity depends on the variation in the scattering length density (SLD)
profile, (ρ(z)) perpendicular to the interface. Although the scattering length density profile
is normally a continuously varying function, the interfacial structure can often be well approximated
by a slab model in which layers of thickness (d_n), scattering length density (ρ_n) and roughness (σ_n,n+1) are sandwiched between the super- and sub-phases. One then uses a refinement procedure to minimise the differences between the theoretical and measured reflectivity curves, by changing the parameters that describe each layer.

In this description the interface is split into n layers. Since the incident neutron beam
is refracted by each of the layers the wavevector, k, in layer n, is given by:

The Fresnel reflection

Fresnel equations

The Fresnel equations , deduced by Augustin-Jean Fresnel , describe the behaviour of light when moving between media of differing refractive indices...

 coefficient between layer n and n+1 is then given by:


Since the interface between each layer is unlikely to be perfectly smooth the roughness/diffuseness of each interface modifies the Fresnel coefficient and is accounted for by an error function

Error function

In mathematics, the error function is a special function of sigmoid shape which occurs in probability, statistics and partial differential equations...

, as described by Nevot and Croce (1980).



A phase factor, β is introduced, which accounts for the thickness of each layer.



where .
A characteristic matrix, c_n is then calculated for each layer.


The resultant matrix is defined as the product of these characteristic matrices


from which the reflectivity is calculated

Abeles matrix formalism

• O. S. Heavens. Optical Properties of Thin Films. Butterworth, London (1955).
• L. Nevot, P. Croce, Revue de physique appliquée, 15, 761 (1980).
• F. Abeles, Le Journal de Physique et le Radium, "La théorie générale des couches minces", 11, 307–310 (1950).

Derivations and explanations

• Lecture notes by Bo Sernelius, see Lecture 13. This derivation is more general than the one above, including light that is incident at a non-normal angle, and with specific light polarizations.

Computer programs

There are a number of computer programs that implement this calculation:

• FreeSnell is a stand-alone computer program that implements the transfer-matrix method, including more advanced aspects such as granular films.
• Thinfilm is a web interface that implements the transfer-matrix method, outputting reflection and transmission coefficients, and also ellipsometric parameters Psi and Delta.
• Luxpop.com is another web interface that implements the transfer-matrix method.
• Transfer-matrix calculating program, written in Mathematica.