Tree walking automaton
Encyclopedia
A tree walking automaton (TWA) is a type of finite automaton that deals with tree structures
rather than strings. The concept was originally proposed in .
The following article deals with tree walking automata. For a different notion of tree automaton, closely related to regular tree languages, see branching automaton
.
.
Informally, a tree walking automaton A (TWA) is a finite state device which walks over the tree in a sequential manner. At each moment A visits node v in state q. Depending on the state q, the label of the node v, and whether the node is the root, a left child, a right child or a leaf, A changes its state from q to q' and moves to the parent of v or its left or right child. A TWA accepts a tree if it enters an accepting state, and rejects if its enters a rejecting state or makes an infinite loop. As with string automata, a TWA may be deterministic or nondeterministic.
More formally, a (nondeterministic) tree walking automaton over alphabet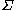
is a tuple:
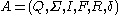
where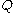
is a finite set of states, 
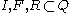are the sets of respectively initial, accepting and rejecting states, and 
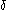is the transition relation: 
.
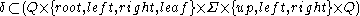(DFS) on the input tree. The automaton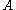
has 3 states, 
. 
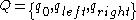begins in the root in state 
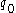and descends to the left subtree. Then it processes the tree recursively. Whenever 
enters a node 
in state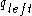 
, it means that the left subtree of 
has just been processed, so it proceeds to the right subtree of 
. If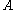 
enters a node 
in state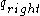 
, it means that the whole subtree with root 
has been processed and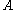 
walks to the parent of 
and changes its state to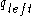 
or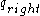 
, depending on whether 
is a left or right child.
, tree walking automata are difficult to analyze and even simple properties are nontrivial to prove. The following list summarizes some known facts related to TWA:
Tree structure
A tree structure is a way of representing the hierarchical nature of a structure in a graphical form. It is named a "tree structure" because the classic representation resembles a tree, even though the chart is generally upside down compared to an actual tree, with the "root" at the top and the...
rather than strings. The concept was originally proposed in .
The following article deals with tree walking automata. For a different notion of tree automaton, closely related to regular tree languages, see branching automaton
Tree automaton
A tree automaton is a type of state machine. Tree automata deal with tree structures, rather than the strings of more conventional state machines.The following article deals with branching tree automata, which correspond to regular languages of trees...
.
Definition
All trees are assumed to be binary, with labels from a fixed alphabet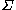.Informally, a tree walking automaton A (TWA) is a finite state device which walks over the tree in a sequential manner. At each moment A visits node v in state q. Depending on the state q, the label of the node v, and whether the node is the root, a left child, a right child or a leaf, A changes its state from q to q' and moves to the parent of v or its left or right child. A TWA accepts a tree if it enters an accepting state, and rejects if its enters a rejecting state or makes an infinite loop. As with string automata, a TWA may be deterministic or nondeterministic.
More formally, a (nondeterministic) tree walking automaton over alphabet
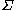is a tuple: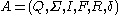where
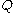is a finite set of states, 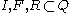are the sets of respectively initial, accepting and rejecting states, and 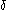is the transition relation: 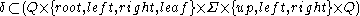.Example
A simple example of a tree walking automaton is a TWA that performs depth-first searchDepth-first search
Depth-first search is an algorithm for traversing or searching a tree, tree structure, or graph. One starts at the root and explores as far as possible along each branch before backtracking....
(DFS) on the input tree. The automaton
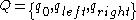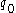has 3 states, . begins in the root in state and descends to the left subtree. Then it processes the tree recursively. Whenever 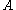enters a node in state 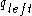, it means that the left subtree of has just been processed, so it proceeds to the right subtree of . If 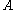enters a node in state 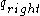, it means that the whole subtree with root has been processed and 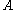walks to the parent of and changes its state to 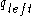or 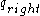, depending on whether is a left or right child.Properties
Unlike branching automataTree automaton
A tree automaton is a type of state machine. Tree automata deal with tree structures, rather than the strings of more conventional state machines.The following article deals with branching tree automata, which correspond to regular languages of trees...
, tree walking automata are difficult to analyze and even simple properties are nontrivial to prove. The following list summarizes some known facts related to TWA:
- As shown by , deterministic TWA are strictly weaker than nondeterministic ones (
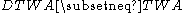) - deterministic TWA are closed under complementation (but it is not known whether the same holds for nondeterministic ones)
- the set of languages recognized by TWA is strictly contained in regular tree languages (
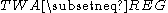), i.e. there exist regular languages which are not recognized by any tree walking automaton .
External links
- Mikołaj Bojanczyk: Tree-walking automata. A brief survey.