Turbulent Kinetic Energy
Encyclopedia
In fluid dynamics
, turbulence kinetic energy (TKE) is the mean kinetic energy
per unit mass associated with eddies
in turbulent flow. Physically, the turbulence kinetic energy is characterised by measured root-mean-square (RMS) velocity fluctuations.
In Reynolds-averaged Navier Stokes equations, the turbulence kinetic energy can be calculated based on the closure method, i.e. a turbulence model. Generally, the TKE can be quantified by the mean of the turbulence normal stresses:
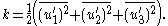
TKE can be produced by fluid shear, friction or buoyancy, or through external forcing at low-frequency eddie scales(integral scale). Turbulence kinetic energy is then transferred down the turbulence energy cascade, and is dissipated by viscous forces at the Kolmogorov scale. This process of production, transport and dissipation can be expressed as:
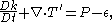
where:
By examining these phenomena, the turbulence kinetic energy budget for a particular flow can be found .
(CFD), it is impossible to numerically simulate turbulence without discretising the flow-field as far as the Kolmogorov microscales
, which is called direct numerical simulation
(DNS). Because DNS simulations are exorbitantly expensive due to memory, computational and storage overheads, turbulence models are used to simulate the effects of turbulence. A variety of models are used, but generally TKE is a fundamental flow property which must be calculated in order for fluid turbulence to be modelled.
where
The exact method of resolving TKE depends upon the turbulence model used; k-ε (k–epsilon) models assume isotropy of turbulence whereby the normal stresses are equal:
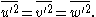
This assumption makes modelling of turbulence quantities (k and
) simpler, but will not be accurate in scenarios where anisotropic behaviour of turbulence stresses dominates, and the implications of this in the production of turbulence also leads to over-prediction since the production depends on the mean rate of strain, and not the difference between the normal stresses (as they are, by assumption, equal) .
Reynolds-stress
models (RSM) use a different method to close the Reynolds stresses, whereby the normal stresses are not assumed isotropic, so the issue with TKE production is avoided.
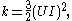
where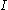
is the initial turbulence intensity [%] given below, and
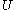is the initial velocity magnitude;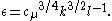
Here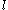
is the turbulence or eddy length scale, give below, and
is a k-ε model parameter whose value is typically given as 0.09;
Further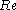
is the Reynolds number
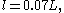
with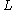
a characteristic length. For internal flows this may take the value of the inlet duct (or pipe) width (or diameter) or the hydraulic diameter.
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, turbulence kinetic energy (TKE) is the mean kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
per unit mass associated with eddies
Eddy (fluid dynamics)
In fluid dynamics, an eddy is the swirling of a fluid and the reverse current created when the fluid flows past an obstacle. The moving fluid creates a space devoid of downstream-flowing fluid on the downstream side of the object...
in turbulent flow. Physically, the turbulence kinetic energy is characterised by measured root-mean-square (RMS) velocity fluctuations.
In Reynolds-averaged Navier Stokes equations, the turbulence kinetic energy can be calculated based on the closure method, i.e. a turbulence model. Generally, the TKE can be quantified by the mean of the turbulence normal stresses:
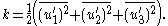
TKE can be produced by fluid shear, friction or buoyancy, or through external forcing at low-frequency eddie scales(integral scale). Turbulence kinetic energy is then transferred down the turbulence energy cascade, and is dissipated by viscous forces at the Kolmogorov scale. This process of production, transport and dissipation can be expressed as:
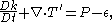
where:
-
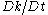is the mean-flow material derivative of TKE; -
is the turbulence transport of TKE; -
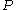is the production of TKE, and -
is the TKE dissipation.
By examining these phenomena, the turbulence kinetic energy budget for a particular flow can be found .
Computational fluid dynamics
In computational fluid dynamicsComputational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
(CFD), it is impossible to numerically simulate turbulence without discretising the flow-field as far as the Kolmogorov microscales
Kolmogorov microscales
Kolmogorov microscales are the smallest scales in turbulent flow. They are defined bywhere \epsilon is the average rate of energy dissipation per unit mass, and \nu is the kinematic viscosity of the fluid....
, which is called direct numerical simulation
Direct numerical simulation
A direct numerical simulation is a simulation in computational fluid dynamics in which the Navier-Stokes equations are numerically solved without any turbulence model...
(DNS). Because DNS simulations are exorbitantly expensive due to memory, computational and storage overheads, turbulence models are used to simulate the effects of turbulence. A variety of models are used, but generally TKE is a fundamental flow property which must be calculated in order for fluid turbulence to be modelled.
Reynolds-averaged Navier–Stokes equations
Reynolds-averaged Navier–Stokes (RANS) simulations use the Boussinesq eddy viscosity hypothesis to calculate the Reynolds stresses that result from the averaging procedure:where
The exact method of resolving TKE depends upon the turbulence model used; k-ε (k–epsilon) models assume isotropy of turbulence whereby the normal stresses are equal:
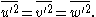
This assumption makes modelling of turbulence quantities (k and
) simpler, but will not be accurate in scenarios where anisotropic behaviour of turbulence stresses dominates, and the implications of this in the production of turbulence also leads to over-prediction since the production depends on the mean rate of strain, and not the difference between the normal stresses (as they are, by assumption, equal) .Reynolds-stress
Reynolds stresses
In fluid dynamics, the Reynolds stress is the stress tensor in a fluid obtained from the averaging operation over the Navier-Stokes equations to account for turbulent fluctuations in fluid momentum.-Definition:...
models (RSM) use a different method to close the Reynolds stresses, whereby the normal stresses are not assumed isotropic, so the issue with TKE production is avoided.
Boundary conditions
Accurate prescription of TKE as boundary conditions in CFD simulations are important to accurately predict flows, especially in high Reynolds-number simulations. Some possible examples are given below.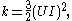where
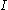is the initial turbulence intensity [%] given below, and 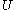is the initial velocity magnitude;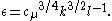Here
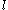is the turbulence or eddy length scale, give below, and is a k-ε model parameter whose value is typically given as 0.09;Further
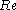is the Reynolds number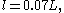with
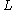a characteristic length. For internal flows this may take the value of the inlet duct (or pipe) width (or diameter) or the hydraulic diameter.External links
- Turbulence kinetic energy at CFD Online.