
Two-moment decision models
Encyclopedia
In decision theory
, economics
, and finance
, a two-moment decision model is a model that describes
or prescribes
the process of making decisions in a context in which the decision-maker is faced with random variable
s whose realizations cannot be known in advance, and in which choices are made based on knowledge of two moments
of those random variables. The two moments are almost always the mean—that is, the expected value
, which is the first moment about zero—and the variance
, which is the second moment about the mean (or the standard deviation
, which is the square root of the variance).
, meaning that the distribution of every random variable is the same as the distribution of some linear transformation of any other random variable. Then for any von Neumann-Morgenstern utility function, using a mean-variance decision framework is consistent with expected utility
maximization, as illustrated in example 1:
Example 1: Let there be one risky asset with random return r, and one riskfree asset with known return rf, and let an investor's initial wealth be w0. If the amount q, the choice variable, is to be invested in the risky asset and the amount w0 – q is to be invested in the safe asset, then contingent on q the investor's random final wealth will be w=(w0 – q)rf + qr. Then for any choice of q, w is distributed as a location-scale transformation of r. If we define random variable x as equal in distribution to then w is equal in distribution to (Ew + σwx), where E represents an expected value and σ represents a random variable's standard deviation
then w is equal in distribution to (Ew + σwx), where E represents an expected value and σ represents a random variable's standard deviation
(the square root of its second moment). Thus we can write expected utility in terms of two moments of w :
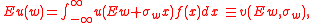
where u is the von Neumann-Morgenstern utility function, f is the density function of x, and v is the derived mean-standard deviation choice function, which depends in form on the density function f. The von Neumann-Morgenstern utility function is assumed to be increasing, implying that more wealth is preferred to less, and it is assumed to be concave, which is the same as assuming that the individual is risk averse
.
It can be shown that the partial derivative of v with respect to Ew is positive, and the partial derivative of v with respect to σw is negative; thus more expected wealth is always liked, and more risk (as measured by the standard deviation of wealth) is always disliked. A mean-standard deviation indifference curve
is defined as the locus of points (σw , Ew) with σw plotted horizontally, such that Eu(w) has the same value at all points on the locus. Then the derivatives of v imply that every indifference curve is upward sloped: that is, along any indifference curve dEw / dσw > 0. Moreover, it can be shown that all such indifference curves are convex: along any indifference curve, d2Ew / d(σw)2 > 0.
Example 2: The portfolio analysis in example 1 can be generalized. If there are n risky assets instead of just one, and if their returns are jointly elliptically distributed
, then all portfolios can be characterized completely by their mean and variance—that is, any two portfolios with identical mean and variance of portfolio return have identical distributions of portfolio return—and all possible portfolios have return distributions that are location-scale-related to each other. Thus portfolio optimization can be implemented using a two-moment decision model.
Example 3: Suppose that a price-taking
, risk-averse
firm must commit to producing a quantity of output q before observing the market realization p of the product's price. Its decision problem is to choose q so as to maximize the expected utility of profit:
where E is the expected value
operator, u is the firm's utility function, c is its variable cost function
, and g is its fixed cost
. All possible distributions of the firm's random revenue pq, based on all possible choices of q, are location-scale related; so the decision problem can be framed in terms of the expected value and variance of revenue.
, decision-making can still be framed in terms of the mean and variance of a random variable if all alternative distributions for an unpredictable outcome are location-scale transformations of each other.
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
, economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, and finance
Finance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
, a two-moment decision model is a model that describes
Positive economics
Positive economics is the branch of economics that concerns the description and explanation of economic phenomena. It focuses on facts and cause-and-effect behavioral relationships and includes the development and testing of economics theories...
or prescribes
Normative economics
Normative economics is that part of economics that expresses value judgments about economic fairness or what the economy ought to be like or what goals of public policy ought to be....
the process of making decisions in a context in which the decision-maker is faced with random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s whose realizations cannot be known in advance, and in which choices are made based on knowledge of two moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of those random variables. The two moments are almost always the mean—that is, the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
, which is the first moment about zero—and the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
, which is the second moment about the mean (or the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
, which is the square root of the variance).
Two-moment models and expected utility maximization
Suppose that all relevant random variables are in the same location-scale familyLocation-scale family
In probability theory, especially as that field is used in statistics, a location-scale family is a family of univariate probability distributions parametrized by a location parameter and a non-negative scale parameter; if X is any random variable whose probability distribution belongs to such a...
, meaning that the distribution of every random variable is the same as the distribution of some linear transformation of any other random variable. Then for any von Neumann-Morgenstern utility function, using a mean-variance decision framework is consistent with expected utility
Expected utility hypothesis
In economics, game theory, and decision theory the expected utility hypothesis is a theory of utility in which "betting preferences" of people with regard to uncertain outcomes are represented by a function of the payouts , the probabilities of occurrence, risk aversion, and the different utility...
maximization, as illustrated in example 1:
Example 1: Let there be one risky asset with random return r, and one riskfree asset with known return rf, and let an investor's initial wealth be w0. If the amount q, the choice variable, is to be invested in the risky asset and the amount w0 – q is to be invested in the safe asset, then contingent on q the investor's random final wealth will be w=(w0 – q)rf + qr. Then for any choice of q, w is distributed as a location-scale transformation of r. If we define random variable x as equal in distribution to
 then w is equal in distribution to (Ew + σwx), where E represents an expected value and σ represents a random variable's standard deviation
then w is equal in distribution to (Ew + σwx), where E represents an expected value and σ represents a random variable's standard deviationStandard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
(the square root of its second moment). Thus we can write expected utility in terms of two moments of w :
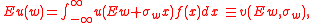
where u is the von Neumann-Morgenstern utility function, f is the density function of x, and v is the derived mean-standard deviation choice function, which depends in form on the density function f. The von Neumann-Morgenstern utility function is assumed to be increasing, implying that more wealth is preferred to less, and it is assumed to be concave, which is the same as assuming that the individual is risk averse
Risk aversion
Risk aversion is a concept in psychology, economics, and finance, based on the behavior of humans while exposed to uncertainty....
.
It can be shown that the partial derivative of v with respect to Ew is positive, and the partial derivative of v with respect to σw is negative; thus more expected wealth is always liked, and more risk (as measured by the standard deviation of wealth) is always disliked. A mean-standard deviation indifference curve
Indifference curve
In microeconomic theory, an indifference curve is a graph showing different bundles of goods between which a consumer is indifferent. That is, at each point on the curve, the consumer has no preference for one bundle over another. One can equivalently refer to each point on the indifference curve...
is defined as the locus of points (σw , Ew) with σw plotted horizontally, such that Eu(w) has the same value at all points on the locus. Then the derivatives of v imply that every indifference curve is upward sloped: that is, along any indifference curve dEw / dσw > 0. Moreover, it can be shown that all such indifference curves are convex: along any indifference curve, d2Ew / d(σw)2 > 0.
Example 2: The portfolio analysis in example 1 can be generalized. If there are n risky assets instead of just one, and if their returns are jointly elliptically distributed
Elliptical distribution
In probability and statistics, an elliptical distribution is any member of a broad family of probability distributions that generalize the multivariate normal distribution and inherit some of its properties.-Definition:...
, then all portfolios can be characterized completely by their mean and variance—that is, any two portfolios with identical mean and variance of portfolio return have identical distributions of portfolio return—and all possible portfolios have return distributions that are location-scale-related to each other. Thus portfolio optimization can be implemented using a two-moment decision model.
Example 3: Suppose that a price-taking
Perfect competition
In economic theory, perfect competition describes markets such that no participants are large enough to have the market power to set the price of a homogeneous product. Because the conditions for perfect competition are strict, there are few if any perfectly competitive markets...
, risk-averse
Risk aversion
Risk aversion is a concept in psychology, economics, and finance, based on the behavior of humans while exposed to uncertainty....
firm must commit to producing a quantity of output q before observing the market realization p of the product's price. Its decision problem is to choose q so as to maximize the expected utility of profit:
- Maximize Eu(pq – c(q) – g),
where E is the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
operator, u is the firm's utility function, c is its variable cost function
Cost curve
In economics, a cost curve is a graph of the costs of production as a function of total quantity produced. In a free market economy, productively efficient firms use these curves to find the optimal point of production , and profit maximizing firms can use them to decide output quantities to...
, and g is its fixed cost
Fixed cost
In economics, fixed costs are business expenses that are not dependent on the level of goods or services produced by the business. They tend to be time-related, such as salaries or rents being paid per month, and are often referred to as overhead costs...
. All possible distributions of the firm's random revenue pq, based on all possible choices of q, are location-scale related; so the decision problem can be framed in terms of the expected value and variance of revenue.
Non-expected-utility decision making
If the decision-maker is not an expected utility maximizerGeneralized expected utility
The expected utility model developed by John von Neumann and Oskar Morgenstern dominated decision theory from its formulation in 1944 until the late 1970s, not only as a prescriptive, but also as a descriptive model, despite powerful criticism from Maurice Allais and Daniel Ellsberg who showed...
, decision-making can still be framed in terms of the mean and variance of a random variable if all alternative distributions for an unpredictable outcome are location-scale transformations of each other.

