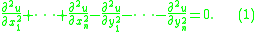Ultrahyperbolic wave equation
Encyclopedia
In the mathematical
field of partial differential equation
s, the ultrahyperbolic equation is a partial differential equation for an unknown scalar function u of 2n variables x1, ..., xn, y1, ..., yn of the form
More generally, if a is any quadratic form
in 2n variables with signature
(n,n), then any PDE whose principal part is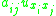 is said to be ultrahyperbolic. Any such equation can be put in the form 1. above by means of a change of variables.
is said to be ultrahyperbolic. Any such equation can be put in the form 1. above by means of a change of variables.
The ultrahyperbolic equation has been studied from a number of viewpoints. On the one hand, it resembles the classical wave equation
. This has led to a number of developments concerning its characteristics
, one of which is due to Fritz John
: the John equation.
The equation has also been studied from the point of view of symmetric space
s, and elliptic differential operators. In particular, the ultrahyperbolic equation satisfies an analog of the mean value theorem for harmonic functions
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s, the ultrahyperbolic equation is a partial differential equation for an unknown scalar function u of 2n variables x1, ..., xn, y1, ..., yn of the form
More generally, if a is any quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
in 2n variables with signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
(n,n), then any PDE whose principal part is
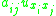 is said to be ultrahyperbolic. Any such equation can be put in the form 1. above by means of a change of variables.
is said to be ultrahyperbolic. Any such equation can be put in the form 1. above by means of a change of variables.The ultrahyperbolic equation has been studied from a number of viewpoints. On the one hand, it resembles the classical wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
. This has led to a number of developments concerning its characteristics
Method of characteristics
In mathematics, the method of characteristics is a technique for solving partial differential equations. Typically, it applies to first-order equations, although more generally the method of characteristics is valid for any hyperbolic partial differential equation...
, one of which is due to Fritz John
Fritz John
Fritz John was a German-born mathematician specialising in partial differential equations and ill-posed problems. His early work was on the Radon transform and he is remembered for John's equation.-Biography:...
: the John equation.
The equation has also been studied from the point of view of symmetric space
Symmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
s, and elliptic differential operators. In particular, the ultrahyperbolic equation satisfies an analog of the mean value theorem for harmonic functions
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....