
Vague topology
Encyclopedia
In mathematics
, particularly in the area of functional analysis
and topological vector space
s, the vague topology is an example of the weak-* topology
which arises in the study of measures on locally compact Hausdorff spaces.
Let X be a locally compact Hausdorff space. Let M(X) be the space of complex Radon measure
s on X, and C0(X)* denote the dual of C0(X), the Banach space
of complex continuous function
s on X vanishing at infinity equipped with the uniform norm. By the Riesz representation theorem
M(X) is isometric
to C0(X)*. The isometry maps a measure μ to a linear functional
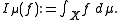
The vague topology is the weak-* topology
on C0(X)*. The corresponding topology on M(X) induced by the isometry from C0(X)* is also called the vague topology on M(X). Thus, in particular, one may refer to vague convergence of measure μn → μ.
One application of this is to probability theory
: for example, the central limit theorem
is essentially a statement that if μn are the probability measure
s for certain sums of independent random variables, then μn converge weakly to a normal distribution, i.e. the measure μn is "approximately normal" for large n.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly in the area of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
s, the vague topology is an example of the weak-* topology
Weak topology
In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
which arises in the study of measures on locally compact Hausdorff spaces.
Let X be a locally compact Hausdorff space. Let M(X) be the space of complex Radon measure
Radon measure
In mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
s on X, and C0(X)* denote the dual of C0(X), the Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
of complex continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s on X vanishing at infinity equipped with the uniform norm. By the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
M(X) is isometric
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
to C0(X)*. The isometry maps a measure μ to a linear functional
Linear functional
In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars. In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
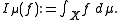
The vague topology is the weak-* topology
Weak topology
In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
on C0(X)*. The corresponding topology on M(X) induced by the isometry from C0(X)* is also called the vague topology on M(X). Thus, in particular, one may refer to vague convergence of measure μn → μ.
One application of this is to probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
: for example, the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
is essentially a statement that if μn are the probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s for certain sums of independent random variables, then μn converge weakly to a normal distribution, i.e. the measure μn is "approximately normal" for large n.

