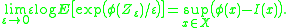Varadhan's lemma
Encyclopedia
In mathematics
, Varadhan's lemma is a result in large deviations theory
named after S. R. Srinivasa Varadhan
. The result gives information on the asymptotic distribution
of a statistic φ(Zε) of a family of random variable
s Zε as ε becomes small in terms of a rate function
for the variables.
; let (Zε)ε>0 be a family of random variables taking values in X; let με be the law (probability measure
) of Zε. Suppose that (με)ε>0 satisfies the large deviation principle with good rate function I : X → [0, +∞]. Let φ : X → R be any continuous function
. Suppose that either one of the following two conditions holds true: either the tail condition
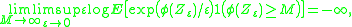
where 1(E) denotes the indicator function of the event E; or, for some γ > 1, the moment
condition
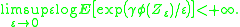
Then
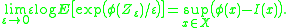
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Varadhan's lemma is a result in large deviations theory
Large deviations theory
In probability theory, the theory of large deviations concerns the asymptotic behaviour of remote tails of sequences of probability distributions. Some basic ideas of the theory can be tracked back to Laplace and Cramér, although a clear unified formal definition was introduced in 1966 by Varadhan...
named after S. R. Srinivasa Varadhan
S. R. Srinivasa Varadhan
Sathamangalam Ranga Iyengar Srinivasa Varadhan FRS is an Indian-American mathematician from Madras , Tamil Nadu, India.-Biography:...
. The result gives information on the asymptotic distribution
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
of a statistic φ(Zε) of a family of random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s Zε as ε becomes small in terms of a rate function
Rate function
In mathematics — specifically, in large deviations theory — a rate function is a function used to quantify the probabilities of rare events. It is required to have several "nice" properties which assist in the formulation of the large deviation principle...
for the variables.
Statement of the lemma
Let X be a regular topological spaceRegular space
In topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
; let (Zε)ε>0 be a family of random variables taking values in X; let με be the law (probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
) of Zε. Suppose that (με)ε>0 satisfies the large deviation principle with good rate function I : X → [0, +∞]. Let φ : X → R be any continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. Suppose that either one of the following two conditions holds true: either the tail condition
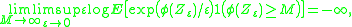
where 1(E) denotes the indicator function of the event E; or, for some γ > 1, the moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
condition
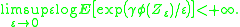
Then