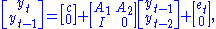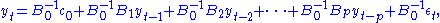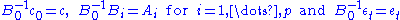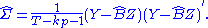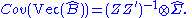Vector autoregression
Encyclopedia
Vector
autoregression (VAR) is a statistical model
used to capture the linear interdependencies among multiple time series
. VAR models generalize the univariate autoregression (AR) models. All the variables in a VAR are treated symmetrically; each variable has an equation explaining its evolution based on its own lag
s and the lags of all the other variables in the model. VAR modeling does not require expert knowledge, which previously had been used in structural models
with simultaneous equations
.
VAR models were advocated by Christopher Sims
, who criticized the claims and performance of earlier modeling in macroeconomic econometrics
. Sims recommended VAR models, which had previously appeared in time series statistics
and system identification
, a statistical specialty in control theory
. Sims advocated VAR models as providing a theory-free method to estimate economic relationships, thus being an alternative to the "incredible identification restrictions" in structural models.. Sims was awarded the 2011 Nobel Prize in Economics for his work in applying VAR models to macroeconomic analysis.
period (t = 1, ..., T) as a linear
function of only their past evolution. The variables are collected in a k × 1 vector
yt, which has as the ith element yi,t the time t observation of variable yi. For example, if the ith variable is GDP, then yi,t is the value of GDP at t.
A (reduced) p-th order VAR, denoted VAR(p), is
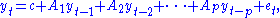
where c is a k × 1 vector of constants (intercept
), Ai is a k × k matrix
(for every i = 1, ..., p) and et is a k × 1 vector of error
terms satisfying
The l-periods back observation yt−l is called the l-th lag of y. Thus, a pth-order VAR is also called a VAR with p lags.
. We have so the following cases:
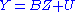
Details of the matrices are in a separate page.
A VAR(1) in two variables can be written in matrix form (more compact notation) as
or, equivalently, as the following system of two equations
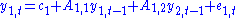
Note that there is one equation for each variable in the model. Also note that the current (time t) observation of each variable depends on its own lags as well as on the lags of each other variable in the VAR.
For example, the VAR(2) model
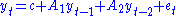
can be recast as the VAR(1) model
where I is the identity matrix
.
The equivalent VAR(1) form is more convenient for analytical derivations and allows more compact statements.
where c0 is a k × 1 vector of constants, Bi is a k × k matrix (for every i = 0, ..., p) and εt is a k × 1 vector of error
terms. The main diagonal terms of the B0 matrix (the coefficients on the ith variable in the ith equation) are scaled to 1.
The error terms εt (structural shocks) satisfy the conditions (1) - (3) in the definition above, with the particularity that all the elements off the main diagonal of the covariance matrix
are zero. That is, the structural shocks are uncorrelated.
For example, a two variable structural VAR(1) is:
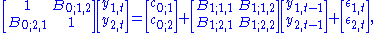
where
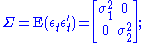
that is, the variance
s of the structural shocks are denoted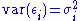
(i = 1, 2) and the covariance
is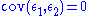
.
Writing the first equation explicitly and passing y2,t to the right hand side one obtains
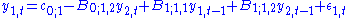
Note that y2,t can have a contemporaneous effect on y1,t if B0;1,2 is not zero. This is different from the case when B0 is the identity matrix
(all off-diagonal elements are zero — the case in the initial definition), when y2,t can impact directly y1,t+1 and subsequent future values, but not y1,t.
Because of the parameter identification problem
, ordinary least squares
estimation of the structural VAR would yield inconsistent parameter estimates. This problem can be overcome by rewriting the VAR in reduced form.
From an economic point of view it is considered that, if the joint dynamics of a set of variables can be represented by a VAR model, then the structural form is a depiction of the underlying, "structural", economic relationships. Two features of the structural form make it the preferred candidate to represent the underlying relations:
and denoting
one obtains the pth order reduced VAR
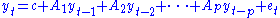
Note that in the reduced form all right hand side variables are predetermined at time t. As there are no time t endogenous variables on the right hand side, no variable has a direct contemporaneous effect on other variables in the model.
However, the error terms in the reduced VAR are composites of the structural shocks et = B0−1εt. Thus, the occurrence of one structural shock εi,t can potentially lead to the occurrence of shocks in all error terms ej,t, thus creating contemporaneous movement in all endogenous variables. Consequently, the covariance matrix of the reduced VAR
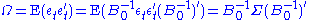
can have non-zero off-diagonal elements, thus allowing non-zero correlation between error terms.
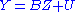
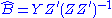
It can be written alternatively as:
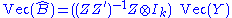
Where
denotes the Kronecker product
and Vec the vectorization
of the matrix Y.
This estimator is consistent and asymptotically efficient. It is furthermore equal to the conditional maximum likelihood estimator
(MLE) (Hamilton 1994, p 293).
MLE estimator:
OLS estimator: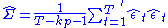
for a model with a constant, k variables and p lags
In a matrix notation, this gives:
Vector
Vector, a Latin word meaning "carrier", may refer in English to:-In computer science:*A one-dimensional array**Vector , a data type in the C++ Standard Template Library...
autoregression (VAR) is a statistical model
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
used to capture the linear interdependencies among multiple time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
. VAR models generalize the univariate autoregression (AR) models. All the variables in a VAR are treated symmetrically; each variable has an equation explaining its evolution based on its own lag
Lag
Lag is a common word meaning to fail to keep up or to fall behind. In real-time applications, the term is used when the application fails to respond in a timely fashion to inputs...
s and the lags of all the other variables in the model. VAR modeling does not require expert knowledge, which previously had been used in structural models
Structural equation modeling
Structural equation modeling is a statistical technique for testing and estimating causal relations using a combination of statistical data and qualitative causal assumptions...
with simultaneous equations
Simultaneous equations model
Simultaneous equation models are a form of statistical model in the form of a set of linear simultaneous equations. They are often used in econometrics.- Structural and reduced form :...
.
VAR models were advocated by Christopher Sims
Christopher A. Sims
Christopher Albert "Chris" Sims is an econometrician and macroeconomist. He is currently the Harold B. Helms Professor of Economics and Banking at Princeton University. Together with Thomas Sargent, he won the Nobel Memorial Prize in Economic Sciences in 2011. The award cited their "empirical...
, who criticized the claims and performance of earlier modeling in macroeconomic econometrics
Econometrics
Econometrics has been defined as "the application of mathematics and statistical methods to economic data" and described as the branch of economics "that aims to give empirical content to economic relations." More precisely, it is "the quantitative analysis of actual economic phenomena based on...
. Sims recommended VAR models, which had previously appeared in time series statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and system identification
System identification
In control engineering, the field of system identification uses statistical methods to build mathematical models of dynamical systems from measured data...
, a statistical specialty in control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
. Sims advocated VAR models as providing a theory-free method to estimate economic relationships, thus being an alternative to the "incredible identification restrictions" in structural models.. Sims was awarded the 2011 Nobel Prize in Economics for his work in applying VAR models to macroeconomic analysis.
Definition
A VAR model describes the evolution of a set of k variables (called endogenous variables) over the same sampleSample (statistics)
In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...
period (t = 1, ..., T) as a linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
function of only their past evolution. The variables are collected in a k × 1 vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
yt, which has as the ith element yi,t the time t observation of variable yi. For example, if the ith variable is GDP, then yi,t is the value of GDP at t.
A (reduced) p-th order VAR, denoted VAR(p), is
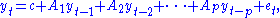
where c is a k × 1 vector of constants (intercept
Intercept
Intercept may refer to:*X-intercept, the point where a line crosses the x-axis*Y-intercept, the point where a line crosses the y-axis*Interception *The Mona Intercept, a 1980 thriller novel by Donald Hamilton...
), Ai is a k × k matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
(for every i = 1, ..., p) and et is a k × 1 vector of error
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
terms satisfying
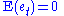— every error term has meanExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
zero;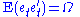
— the contemporaneous covariance matrixCovariance matrixIn probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
of error terms is Ω (a k × k positive definite matrix);
for any non-zero k — there is no correlationCorrelationIn statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
across time; in particular, no serial correlation in individual error terms.
The l-periods back observation yt−l is called the l-th lag of y. Thus, a pth-order VAR is also called a VAR with p lags.
Order of integration of the variables
Note that all the variables used have to be of the same order of integrationOrder of integration
Order of integration, denoted I, is a summary statistic for a time series. It reports the minimum number of differences required to obtain a stationary series.- Integration of order zero :...
. We have so the following cases:
- All the variables are I(0) (stationary): one is in the standard case, i.e. a VAR in level
- All the variables are I(d) (non-stationary) with d>0:
- The variables are cointegratedCointegrationCointegration is a statistical property of time series variables. Two or more time series are cointegrated if they share a common stochastic drift.-Introduction:...
: the error correction term has to be included in the VAR. The model becomes a Vector error correction modelError correction modelAn error correction model is a dynamical system with the characteristics that the deviation of the current state from its long-run relationship will be fed into its short-run dynamics....
(VECM) which can be seen as a restricted VAR. - The variables are not cointegratedCointegrationCointegration is a statistical property of time series variables. Two or more time series are cointegrated if they share a common stochastic drift.-Introduction:...
: the variables have first to be differenced d times and one has a VAR in difference.
- The variables are cointegrated
Concise matrix notation
One can write a VAR(p) with a concise matrix notation: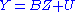Details of the matrices are in a separate page.
Example
For a general example of a VAR(p) with k variables, please see this page.A VAR(1) in two variables can be written in matrix form (more compact notation) as
or, equivalently, as the following system of two equations
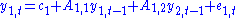
Note that there is one equation for each variable in the model. Also note that the current (time t) observation of each variable depends on its own lags as well as on the lags of each other variable in the VAR.
Writing VAR(p) as VAR(1)
A VAR with p lags can always be equivalently rewritten as a VAR with only one lag by appropriately redefining the dependent variable. The transformation amounts to merely stacking the lags of the VAR(p) variable in the new VAR(1) dependent variable and appending identities to complete the number of equations.For example, the VAR(2) model
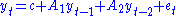
can be recast as the VAR(1) model
where I is the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
.
The equivalent VAR(1) form is more convenient for analytical derivations and allows more compact statements.
Structural VAR
A structural VAR with p lags (sometimes abbreviated SVAR) iswhere c0 is a k × 1 vector of constants, Bi is a k × k matrix (for every i = 0, ..., p) and εt is a k × 1 vector of error
Error
The word error entails different meanings and usages relative to how it is conceptually applied. The concrete meaning of the Latin word "error" is "wandering" or "straying". Unlike an illusion, an error or a mistake can sometimes be dispelled through knowledge...
terms. The main diagonal terms of the B0 matrix (the coefficients on the ith variable in the ith equation) are scaled to 1.
The error terms εt (structural shocks) satisfy the conditions (1) - (3) in the definition above, with the particularity that all the elements off the main diagonal of the covariance matrix
are zero. That is, the structural shocks are uncorrelated.For example, a two variable structural VAR(1) is:
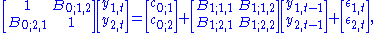
where
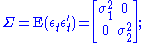
that is, the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
s of the structural shocks are denoted
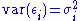(i = 1, 2) and the covarianceCovariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
is
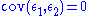.Writing the first equation explicitly and passing y2,t to the right hand side one obtains
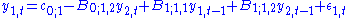
Note that y2,t can have a contemporaneous effect on y1,t if B0;1,2 is not zero. This is different from the case when B0 is the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
(all off-diagonal elements are zero — the case in the initial definition), when y2,t can impact directly y1,t+1 and subsequent future values, but not y1,t.
Because of the parameter identification problem
Parameter identification problem
The parameter identification problem is a problem which can occur in the estimation of multiple-equation econometric models where the equations have variables in common....
, ordinary least squares
Ordinary least squares
In statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...
estimation of the structural VAR would yield inconsistent parameter estimates. This problem can be overcome by rewriting the VAR in reduced form.
From an economic point of view it is considered that, if the joint dynamics of a set of variables can be represented by a VAR model, then the structural form is a depiction of the underlying, "structural", economic relationships. Two features of the structural form make it the preferred candidate to represent the underlying relations:
- 1. Error terms are not correlated. The structural, economic shocks which drive the dynamics of the economic variables are assumed to be independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
, which implies zero correlation between error terms as a desired property. This is helpful for separating out the effects of economically unrelated influences in the VAR. For instance, there is no reason why an oil price shock (as an example of a supply shockSupply shockA supply shock is an event that suddenly changes the price of a commodity or service. It may be caused by a sudden increase or decrease in the supply of a particular good. This sudden change affects the equilibrium price....
) should be related to a shift in consumers' preferences towards a style of clothing (as an example of a demand shockDemand shockIn economics, a demand shock is a sudden event that increases or decreases demand for goods or services temporarily. A positive demand shock increases demand and a negative demand shock decreases demand. Prices of goods and services are affected in both cases. When demand for a good or service...
); therefore one would expect these factors to be statistically independent.
- 2. Variables can have a contemporaneous impact on other variables. This is a desirable feature especially when using low frequency data. For example, an indirect taxIndirect taxThe term indirect tax has more than one meaning.In the colloquial sense, an indirect tax is a tax collected by an intermediary from the person who bears the ultimate economic burden of the tax...
rate increase would not affect tax revenues the day the decision is announced, but one could find an effect in that quarter's data.
Reduced-form VAR
By premultiplying the structural VAR with the inverse of B0
and denoting
one obtains the pth order reduced VAR
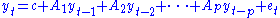
Note that in the reduced form all right hand side variables are predetermined at time t. As there are no time t endogenous variables on the right hand side, no variable has a direct contemporaneous effect on other variables in the model.
However, the error terms in the reduced VAR are composites of the structural shocks et = B0−1εt. Thus, the occurrence of one structural shock εi,t can potentially lead to the occurrence of shocks in all error terms ej,t, thus creating contemporaneous movement in all endogenous variables. Consequently, the covariance matrix of the reduced VAR
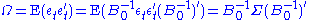
can have non-zero off-diagonal elements, thus allowing non-zero correlation between error terms.
Estimation of the regression parameters
Starting from the concise matrix notation (for details see this annex):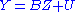- The Multivariate Least Square (MLS) for B yields:
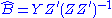
It can be written alternatively as:
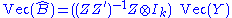
Where
denotes the Kronecker productKronecker product
In mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix...
and Vec the vectorization
Vectorization (mathematics)
In mathematics, especially in linear algebra and matrix theory, the vectorization of a matrix is a linear transformation which converts the matrix into a column vector...
of the matrix Y.
This estimator is consistent and asymptotically efficient. It is furthermore equal to the conditional maximum likelihood estimator
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
(MLE) (Hamilton 1994, p 293).
- As the explanatory variables are the same in each equation, the Multivariate Least Square is equivalent to the Ordinary least squaresLeast squaresThe method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
(OLS) estimator applied to each equation separately, as was shown by Zellner (1962).
Estimation of the covariance matrix of the errors
As in the standard case, the MLE estimator of the covariance matrix differs from the OLS estimator.MLE estimator:
OLS estimator:
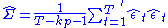for a model with a constant, k variables and p lagsIn a matrix notation, this gives:
Estimation of the estimator's covariance matrix
The covariance matrix of the parameters can be estimated as
Software
- RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
: there is a package vars which deals with VAR models. - SAS: VARMAX
- STATAStataStata is a general-purpose statistical software package created in 1985 by StataCorp. It is used by many businesses and academic institutions around the world...
: "var" - EViewsEViewsEViews is a statistical package for Windows, used mainly for time-series oriented econometric analysis. It is developed by Quantitative Micro Software , now a part of IHS. Version 1.0 was released in March 1994, and replaced MicroTSP...
: "VAR" - GretlGretlgretl is an open-source statistical package, mainly for econometrics. The name is an acronym for Gnu Regression, Econometrics and Time-series Library. It has a graphical user interface and can be used together with X-12-ARIMA, TRAMO/SEATS, R, Octave, and Ox. It is written in C, uses GTK as widget...
: "var" - RATS
- [ARFit]:
- http://biosig-consulting.com/matlab/tsa/ Time Series Analysis toolbox for Octave and Matlab: MVAR