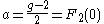Vertex function
Encyclopedia
In quantum electrodynamics
, the vertex function describes the coupling between a photon and an electron beyond the leading order of perturbation theory
. In particular, it is the one particle irreducible correlation function involving the fermion
 , the antifermion
, the antifermion  , and the vector potential
, and the vector potential
A.
of the effective action
Seff as
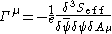
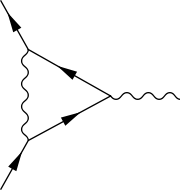 The dominant (and classical) contribution to Γμ is the gamma matrix γμ, which explains the choice of the letter. The vertex function is constrained by the symmetries of quantum electrodynamics -- Lorentz invariance; gauge invariance or the transversality
The dominant (and classical) contribution to Γμ is the gamma matrix γμ, which explains the choice of the letter. The vertex function is constrained by the symmetries of quantum electrodynamics -- Lorentz invariance; gauge invariance or the transversality
of the photon, as expressed by the Ward identity; and invariance under parity
-- to take the following form:
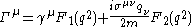
where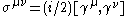 ,
, 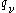 is the incoming four-momentum of the external photon (on the right-hand side of the figure), and F1(q2) and F2(q2) are form factors that depend only on the momentum transfer q2. At tree level (or leading order), F1(q2) = 1 and F2(q2) = 0. Beyond leading order, the corrections to F1(0) are exactly canceled by the wave function renormalization
is the incoming four-momentum of the external photon (on the right-hand side of the figure), and F1(q2) and F2(q2) are form factors that depend only on the momentum transfer q2. At tree level (or leading order), F1(q2) = 1 and F2(q2) = 0. Beyond leading order, the corrections to F1(0) are exactly canceled by the wave function renormalization
of the incoming and outgoing electron lines according to the Ward-Takahashi identity. The form factor F2(0) corresponds to the anomalous magnetic moment a of the fermion, defined in terms of the Lande g-factor
as:
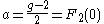
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
, the vertex function describes the coupling between a photon and an electron beyond the leading order of perturbation theory
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
. In particular, it is the one particle irreducible correlation function involving the fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
 , the antifermion
, the antifermion  , and the vector potential
, and the vector potentialVector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
A.
Definition
The vertex function Γμ can be defined in terms of a functional derivativeFunctional derivative
In mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
of the effective action
Effective action
In quantum field theory, the effective action is a modified expression for the action, which takes into account quantum-mechanical corrections, in the following sense:...
Seff as
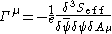

Polarization
Polarization is a property of certain types of waves that describes the orientation of their oscillations. Electromagnetic waves, such as light, and gravitational waves exhibit polarization; acoustic waves in a gas or liquid do not have polarization because the direction of vibration and...
of the photon, as expressed by the Ward identity; and invariance under parity
Parity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
-- to take the following form:
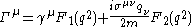
where
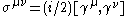 ,
, 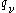 is the incoming four-momentum of the external photon (on the right-hand side of the figure), and F1(q2) and F2(q2) are form factors that depend only on the momentum transfer q2. At tree level (or leading order), F1(q2) = 1 and F2(q2) = 0. Beyond leading order, the corrections to F1(0) are exactly canceled by the wave function renormalization
is the incoming four-momentum of the external photon (on the right-hand side of the figure), and F1(q2) and F2(q2) are form factors that depend only on the momentum transfer q2. At tree level (or leading order), F1(q2) = 1 and F2(q2) = 0. Beyond leading order, the corrections to F1(0) are exactly canceled by the wave function renormalizationWave function renormalization
In quantum field theory, wave function renormalization is a rescaling, or renormalization, of quantum fields to take into account the effects of interactions. For a noninteracting or free field, the field operator creates or annihilates a single particle with probability 1. Once interactions are...
of the incoming and outgoing electron lines according to the Ward-Takahashi identity. The form factor F2(0) corresponds to the anomalous magnetic moment a of the fermion, defined in terms of the Lande g-factor
Landé g-factor
In physics, the Landé g-factor is a particular example of a g-factor, namely for an electron with both spin and orbital angular momenta. It is named after Alfred Landé, who first described it in 1921....
as: