Vibration
Encyclopedia
Vibration refers to mechanical oscillations about an equilibrium point. The oscillations may be periodic
such as the motion of a pendulum or random such as the movement of a tire on a gravel road.
Vibration is occasionally "desirable". For example the motion of a tuning fork
, the reed in a woodwind instrument
or harmonica
, or the cone of a loudspeaker
is desirable vibration, necessary for the correct functioning of the various devices.
More often, vibration is undesirable, wasting energy
and creating unwanted sound
– noise
. For example, the vibrational motions of engine
s, electric motor
s, or any mechanical device
in operation are typically unwanted. Such vibrations can be caused by imbalances
in the rotating parts, uneven friction
, the meshing of gear
teeth, etc. Careful designs usually minimize unwanted vibrations.
The study of sound and vibration are closely related. Sound, or "pressure wave
s", are generated by vibrating structures (e.g. vocal cords); these pressure waves can also induce the vibration of structures (e.g. ear drum). Hence, when trying to reduce noise it is often a problem in trying to reduce vibration.

" and damp down to zero.
Forced vibration is when an alternating force or motion is applied to a mechanical system. Examples of this type of vibration include a shaking washing machine due to an imbalance, transportation vibration (caused by truck engine, springs, road, etc.), or the vibration of a building during an earthquake
. In forced vibration the frequency of the vibration is the frequency of the force or motion applied, with order of magnitude being dependent on the actual mechanical system.
Two typical types of vibration tests performed are random- and sine test. Sine (one-frequency-at-a-time) tests are performed to survey the structural response of the device under test (DUT). A random (all frequencies at once) test is generally considered to more closely replicate a real world environment, such as road inputs to a moving automobile.
Most vibration testing is conducted in a single DUT axis at a time, even though most real-world vibration occurs in various axes simultaneously. MIL-STD-810G, released in late 2008, Test Method 527, calls for multiple exciter testing.
–spring
–damper
model. Indeed, even a complex structure such as an automobile body can be modeled as a "summation" of simple mass–spring–damper models. The mass–spring–damper model is an example of a simple harmonic oscillator. The mathematics used to describe its behavior is identical to other simple harmonic oscillators such as the RLC circuit
.
Note: In this article the step by step mathematical derivations will not be included, but will focus on the major equations and concepts in vibration analysis. Please refer to the references at the end of the article for detailed derivations.
 To start the investigation of the mass–spring–damper we will assume the damping is negligible and that there is no external force applied to the mass (i.e. free vibration).
To start the investigation of the mass–spring–damper we will assume the damping is negligible and that there is no external force applied to the mass (i.e. free vibration).
The force applied to the mass by the spring is proportional to the amount the spring is stretched "x" (we will assume the spring is already compressed due to the weight of the mass). The proportionality constant, k, is the stiffness of the spring and has units of force/distance (e.g. lbf/in or N/m). The negative sign indicates that the force is always opposing the motion of the mass attached to it.

The force generated by the mass is proportional to the acceleration of the mass as given by Newton’s second law of motion
.

The sum of the forces on the mass then generates this ordinary differential equation
:

 If we assume that we start the system to vibrate by stretching the spring by the distance of A and letting go, the solution to the above equation that describes the motion of mass is:
If we assume that we start the system to vibrate by stretching the spring by the distance of A and letting go, the solution to the above equation that describes the motion of mass is:

This solution says that it will oscillate with simple harmonic motion
that has an amplitude
of A and a frequency of The number
The number  is one of the most important quantities in vibration analysis and is called the undamped natural frequency. For the simple mass–spring system,
is one of the most important quantities in vibration analysis and is called the undamped natural frequency. For the simple mass–spring system,  is defined as:
is defined as:

Note: Angular frequency
 (
( ) with the units of radians per second is often used in equations because it simplifies the equations, but is normally converted to “standard” frequency (units of Hz
) with the units of radians per second is often used in equations because it simplifies the equations, but is normally converted to “standard” frequency (units of Hz
or equivalently cycles per second) when stating the frequency of a system.
If you know the mass and stiffness of the system you can determine the frequency at which the system will vibrate once it is set in motion by an initial disturbance using the above stated formula. Every vibrating system has one or more natural frequencies that it will vibrate at once it is disturbed. This simple relation can be used to understand in general what will happen to a more complex system once we add mass or stiffness. For example, the above formula explains why when a car or truck is fully loaded the suspension will feel “softer” than unloaded because the mass has increased and therefore reduced the natural frequency of the system.
. In the above example we have extended the spring by a value of and therefore have stored some potential energy
and therefore have stored some potential energy
( ) in the spring. Once we let go of the spring, the spring tries to return to its un-stretched state (which is the minimum potential energy state) and in the process accelerates the mass. At the point where the spring has reached its un-stretched state all the potential energy that we supplied by stretching it has been transformed into kinetic energy
) in the spring. Once we let go of the spring, the spring tries to return to its un-stretched state (which is the minimum potential energy state) and in the process accelerates the mass. At the point where the spring has reached its un-stretched state all the potential energy that we supplied by stretching it has been transformed into kinetic energy
( ). The mass then begins to decelerate because it is now compressing the spring and in the process transferring the kinetic energy back to its potential. Thus oscillation of the spring amounts to the transferring back and forth of the kinetic energy into potential energy.
). The mass then begins to decelerate because it is now compressing the spring and in the process transferring the kinetic energy back to its potential. Thus oscillation of the spring amounts to the transferring back and forth of the kinetic energy into potential energy.
In our simple model the mass will continue to oscillate forever at the same magnitude, but in a real system there is always something called damping that dissipates the energy, eventually bringing it to rest.
 We now add a "viscous" damper to the model that outputs a force that is proportional to the velocity of the mass. The damping is called viscous because it models the effects of an object within a fluid. The proportionality constant c is called the damping coefficient and has units of Force over velocity (lbf s/ in or N s/m).
We now add a "viscous" damper to the model that outputs a force that is proportional to the velocity of the mass. The damping is called viscous because it models the effects of an object within a fluid. The proportionality constant c is called the damping coefficient and has units of Force over velocity (lbf s/ in or N s/m).

By summing the forces on the mass we get the following ordinary differential equation:

The solution to this equation depends on the amount of damping. If the damping is small enough the system will still vibrate, but eventually, over time, will stop vibrating. This case is called underdamping – this case is of most interest in vibration analysis. If we increase the damping just to the point where the system no longer oscillates we reach the point of critical damping (if the damping is increased past critical damping the system is called overdamped). The value that the damping coefficient needs to reach for critical damping in the mass spring damper model is:

To characterize the amount of damping in a system a ratio called the damping ratio
(also known as damping factor and % critical damping) is used. This damping ratio is just a ratio of the actual damping over the amount of damping required to reach critical damping. The formula for the damping ratio ( ) of the mass spring damper model is:
) of the mass spring damper model is:

For example, metal structures (e.g. airplane fuselage, engine crankshaft) will have damping factors less than 0.05 while automotive suspensions in the range of 0.2–0.3.
The solution to the underdamped system for the mass spring damper model is the following:

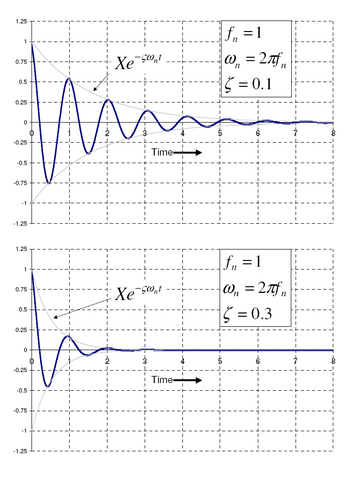 The value of X, the initial magnitude, and
The value of X, the initial magnitude, and  the phase shift, are determined by the amount the spring is stretched. The formulas for these values can be found in the references.
the phase shift, are determined by the amount the spring is stretched. The formulas for these values can be found in the references.
The frequency in this case is called the "damped natural frequency", and is related to the undamped natural frequency by the following formula:
and is related to the undamped natural frequency by the following formula:

The damped natural frequency is less than the undamped natural frequency, but for many practical cases the damping ratio is relatively small and hence the difference is negligible. Therefore the damped and undamped description are often dropped when stating the natural frequency (e.g. with 0.1 damping ratio, the damped natural frequency is only 1% less than the undamped).
The plots to the side present how 0.1 and 0.3 damping ratios effect how the system will “ring” down over time. What is often done in practice is to experimentally measure the free vibration after an impact (for example by a hammer) and then determine the natural frequency of the system by measuring the rate of oscillation as well as the damping ratio by measuring the rate of decay. The natural frequency and damping ratio are not only important in free vibration, but also characterize how a system will behave under forced vibration.

If we again sum the forces on the mass we get the following ordinary differential equation:

The steady state
solution of this problem can be written as:

The result states that the mass will oscillate at the same frequency, f, of the applied force, but with a phase shift
The amplitude of the vibration “X” is defined by the following formula.

Where “r” is defined as the ratio of the harmonic force frequency over the undamped natural frequency of the mass–spring–damper model.

The phase shift , is defined by the following formula.
is defined by the following formula.

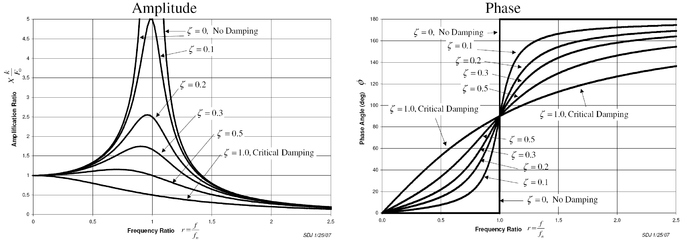 The plot of these functions, called "the frequency response of the system", presents one of the most important features in forced vibration. In a lightly damped system when the forcing frequency nears the natural frequency (
The plot of these functions, called "the frequency response of the system", presents one of the most important features in forced vibration. In a lightly damped system when the forcing frequency nears the natural frequency ( ) the amplitude of the vibration can get extremely high. This phenomenon is called resonance
) the amplitude of the vibration can get extremely high. This phenomenon is called resonance
(subsequently the natural frequency of a system is often referred to as the resonant frequency). In rotor bearing systems any rotational speed that excites a resonant frequency is referred to as a critical speed
.
If resonance occurs in a mechanical system it can be very harmful – leading to eventual failure of the system. Consequently, one of the major reasons for vibration analysis is to predict when this type of resonance may occur and then to determine what steps to take to prevent it from occurring. As the amplitude plot shows, adding damping can significantly reduce the magnitude of the vibration. Also, the magnitude can be reduced if the natural frequency can be shifted away from the forcing frequency by changing the stiffness or mass of the system. If the system cannot be changed, perhaps the forcing frequency can be shifted (for example, changing the speed of the machine generating the force).
The following are some other points in regards to the forced vibration shown in the frequency response plots.
The damper, instead of storing energy, dissipates energy. Since the damping force is proportional to the velocity, the more the motion, the more the damper dissipates the energy. Therefore a point will come when the energy dissipated by the damper will equal the energy being fed in by the force. At this point, the system has reached its maximum amplitude and will continue to vibrate at this level as long as the force applied stays the same. If no damping exists, there is nothing to dissipate the energy and therefore theoretically the motion will continue to grow on into infinity.
that takes a signal as a function of time (time domain
) and breaks it down into its harmonic components as a function of frequency (frequency domain
). For example, let us apply a force to the mass–spring–damper model that repeats the following cycle – a force equal to 1 newton for 0.5 second and then no force for 0.5 second. This type of force has the shape of a 1 Hz square wave
.
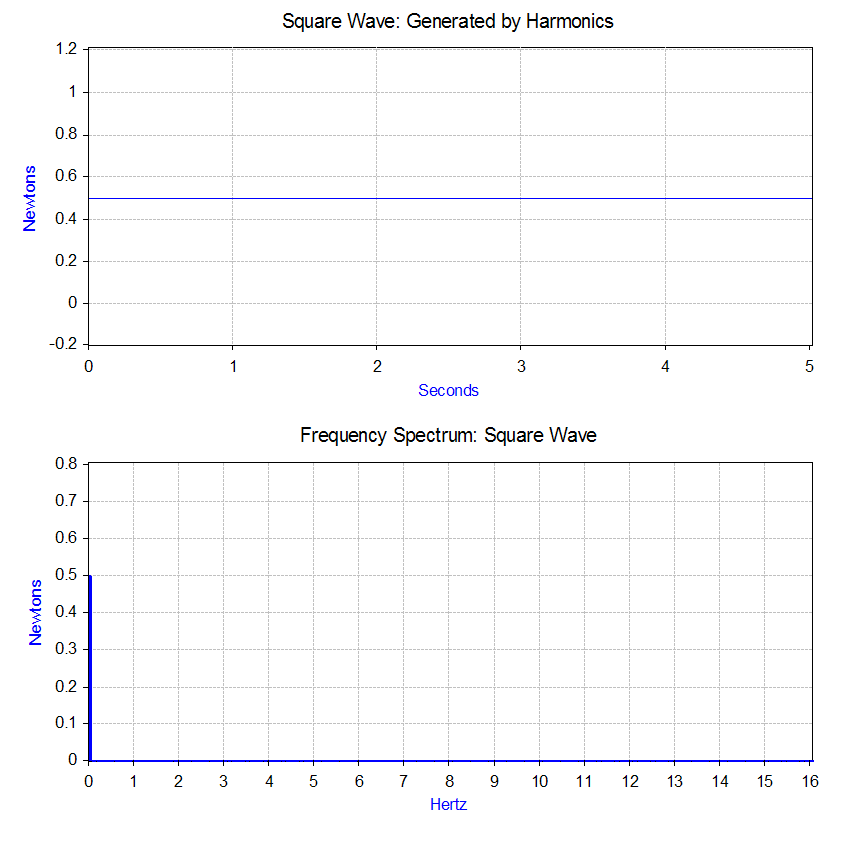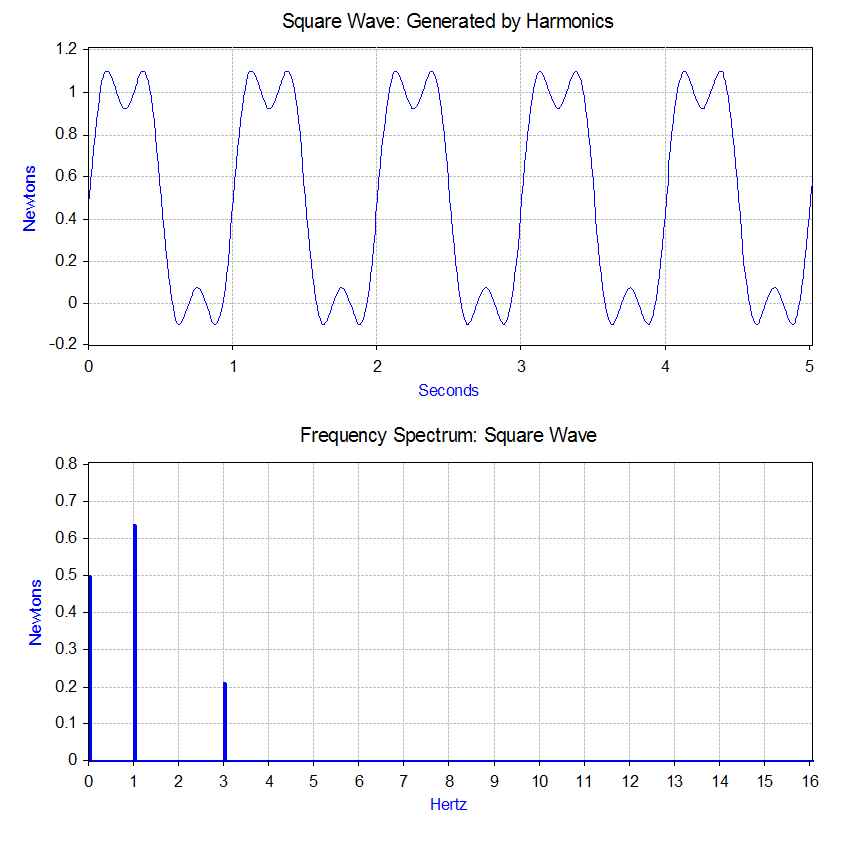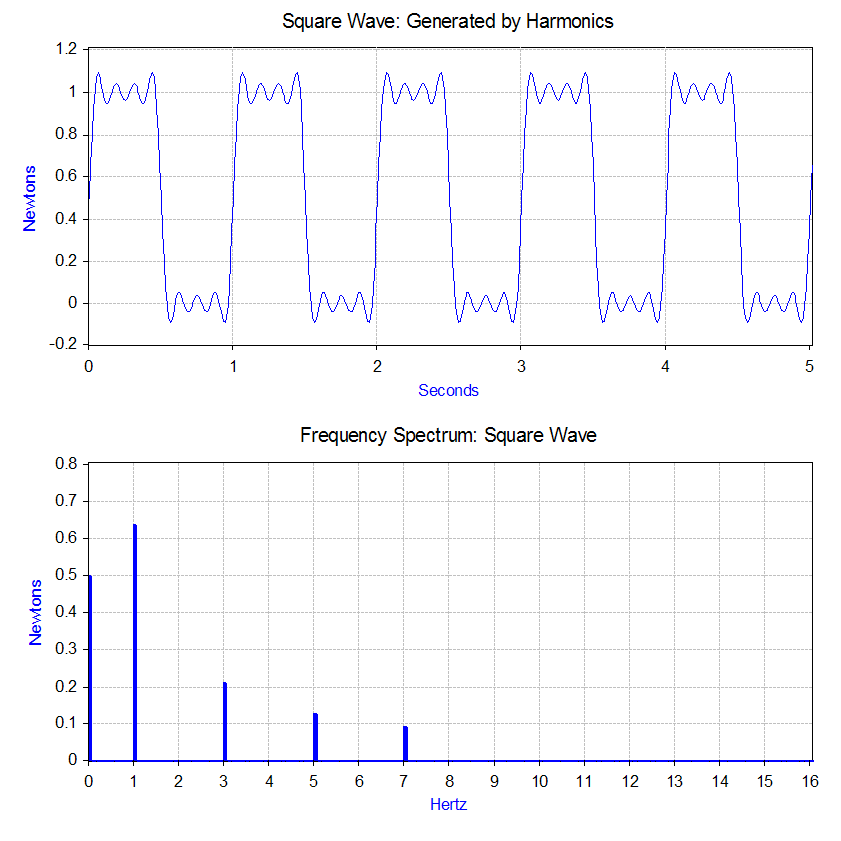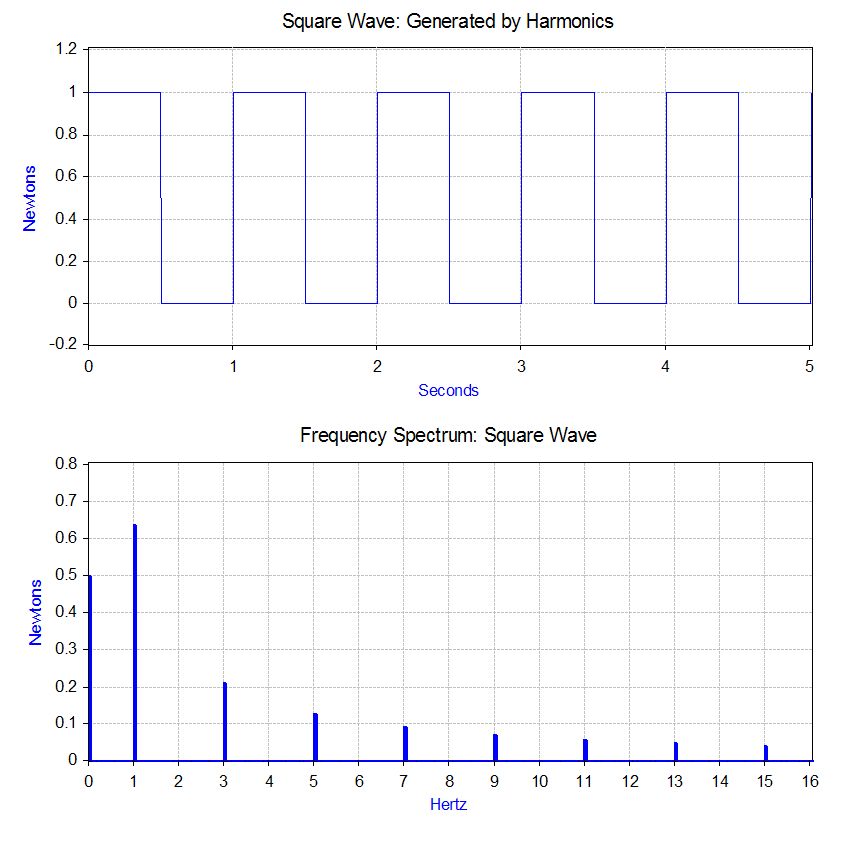 The Fourier transform of the square wave generates a frequency spectrum
The Fourier transform of the square wave generates a frequency spectrum
that presents the magnitude of the harmonics that make up the square wave (the phase is also generated, but is typically of less concern and therefore is often not plotted). The Fourier transform can also be used to analyze non-periodic
functions such as transients (e.g. impulses) and random functions. With the advent of the modern computer the Fourier transform is almost always computed using the Fast Fourier Transform
(FFT) computer algorithm in combination with a window function
.
In the case of our square wave force, the first component is actually a constant force of 0.5 newton and is represented by a value at "0" Hz in the frequency spectrum. The next component is a 1 Hz sine wave with an amplitude of 0.64. This is shown by the line at 1 Hz. The remaining components are at odd frequencies and it takes an infinite amount of sine waves to generate the perfect square wave. Hence, the Fourier transform allows you to interpret the force as a sum of sinusoidal forces being applied instead of a more "complex" force (e.g. a square wave).
In the previous section, the vibration solution was given for a single harmonic force, but the Fourier transform will in general give multiple harmonic forces. The second mathematical tool, "the principle of superposition"
, allows you to sum the solutions from multiple forces if the system is linear
. In the case of the spring–mass–damper model, the system is linear if the spring force is proportional to the displacement and the damping is proportional to the velocity over the range of motion of interest. Hence, the solution to the problem with a square wave is summing the predicted vibration from each one of the harmonic forces found in the frequency spectrum of the square wave.

 is called the frequency response
is called the frequency response
function (also referred to as the transfer function
, but not technically as accurate) and has both a magnitude and phase component (if represented as a complex number
, a real and imaginary component). The magnitude of the frequency response function (FRF) was presented earlier for the mass–spring–damper system.
 where
where 
The phase of the FRF was also presented earlier as:

For example, let us calculate the FRF for a mass–spring–damper system with a mass of 1 kg, spring stiffness of 1.93 N/mm and a damping ratio of 0.1. The values of the spring and mass give a natural frequency of 7 Hz for this specific system. If we apply the 1 Hz square wave from earlier we can calculate the predicted vibration of the mass. The figure illustrates the resulting vibration. It happens in this example that the fourth harmonic of the square wave falls at 7 Hz. The frequency response of the mass–spring–damper therefore outputs a high 7 Hz vibration even though the input force had a relatively low 7 Hz harmonic. This example highlights that the resulting vibration is dependent on both the forcing function and the system that the force is applied to.
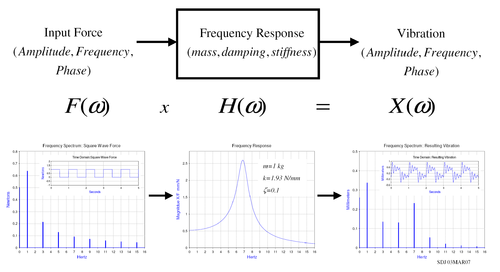 The figure also shows the time domain representation of the resulting vibration. This is done by performing an inverse Fourier Transform that converts frequency domain data to time domain. In practice, this is rarely done because the frequency spectrum provides all the necessary information.
The figure also shows the time domain representation of the resulting vibration. This is done by performing an inverse Fourier Transform that converts frequency domain data to time domain. In practice, this is rarely done because the frequency spectrum provides all the necessary information.
The frequency response function (FRF) does not necessarily have to be calculated from the knowledge of the mass, damping, and stiffness of the system, but can be measured experimentally. For example, if you apply a known force and sweep the frequency and then measure the resulting vibration you can calculate the frequency response function and then characterize the system. This technique is used in the field of experimental modal analysis
to determine the vibration characteristics of a structure.
(SDOF) model since we have assumed the mass only moves up and down. In the case of more complex systems we need to discretize the system into more masses and allow them to move in more than one direction – adding degrees of freedom. The major concepts of multiple degrees of freedom (MDOF) can be understood by looking at just a 2 degree of freedom model as shown in the figure.
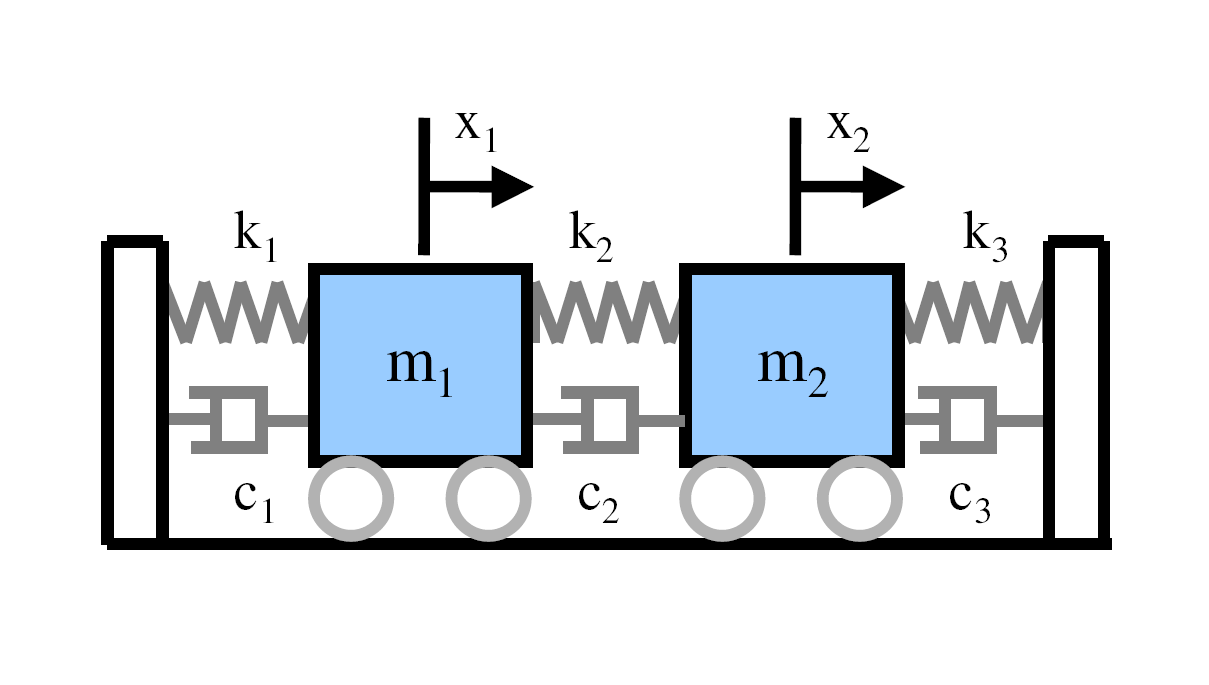 The equations of motion of the 2DOF system are found to be:
The equations of motion of the 2DOF system are found to be:


We can rewrite this in matrix
format:

A more compact form of this matrix equation can be written as:

where
 and
and  are symmetric matrices referred respectively as the mass, damping, and stiffness matrices. The matrices are NxN square matrices where N is the number of degrees of freedom of the system.
are symmetric matrices referred respectively as the mass, damping, and stiffness matrices. The matrices are NxN square matrices where N is the number of degrees of freedom of the system.
In the following analysis we will consider the case where there is no damping and no applied forces (i.e. free vibration). The solution of a viscously damped system is somewhat more complicated.

This differential equation can be solved by assuming the following type of solution:

Note: Using the exponential solution of is a mathematical trick used to solve linear differential equations. If we use Euler's formula
is a mathematical trick used to solve linear differential equations. If we use Euler's formula
and take only the real part of the solution it is the same cosine solution for the 1 DOF system. The exponential solution is only used because it easier to manipulate mathematically.
The equation then becomes:

Since cannot equal zero the equation reduces to the following.
cannot equal zero the equation reduces to the following.



and if we let and
and 

The solution to the problem results in N eigenvalues (i.e. ), where N corresponds to the number of degrees of freedom. The eigenvalues provide the natural frequencies of the system. When these eigenvalues are substituted back into the original set of equations, the values of
), where N corresponds to the number of degrees of freedom. The eigenvalues provide the natural frequencies of the system. When these eigenvalues are substituted back into the original set of equations, the values of  that correspond to each eigenvalue are called the eigenvectors. These eigenvectors represent the mode shapes of the system. The solution of an eigenvalue problem can be quite cumbersome (especially for problems with many degrees of freedom), but fortunately most math analysis programs have eigenvalue routines.
that correspond to each eigenvalue are called the eigenvectors. These eigenvectors represent the mode shapes of the system. The solution of an eigenvalue problem can be quite cumbersome (especially for problems with many degrees of freedom), but fortunately most math analysis programs have eigenvalue routines.
The eigenvalues and eigenvectors are often written in the following matrix format and describe the modal model of the system:
 and
and 
A simple example using our 2 DOF model can help illustrate the concepts. Let both masses have a mass of 1 kg and the stiffness of all three springs equal 1000 N/m. The mass and stiffness matrix for this problem are then:
 and
and 
Then
The eigenvalues for this problem given by an eigenvalue routine will be:

The natural frequencies in the units of hertz are then (remembering )
)  and
and  .
.
The two mode shapes for the respective natural frequencies are given as:

Since the system is a 2 DOF system, there are two modes with their respective natural frequencies and shapes. The mode shape vectors are not the absolute motion, but just describe relative motion of the degrees of freedom. In our case the first mode shape vector is saying that the masses are moving together in phase since they have the same value and sign. In the case of the second mode shape vector, each mass is moving in opposite direction at the same rate.
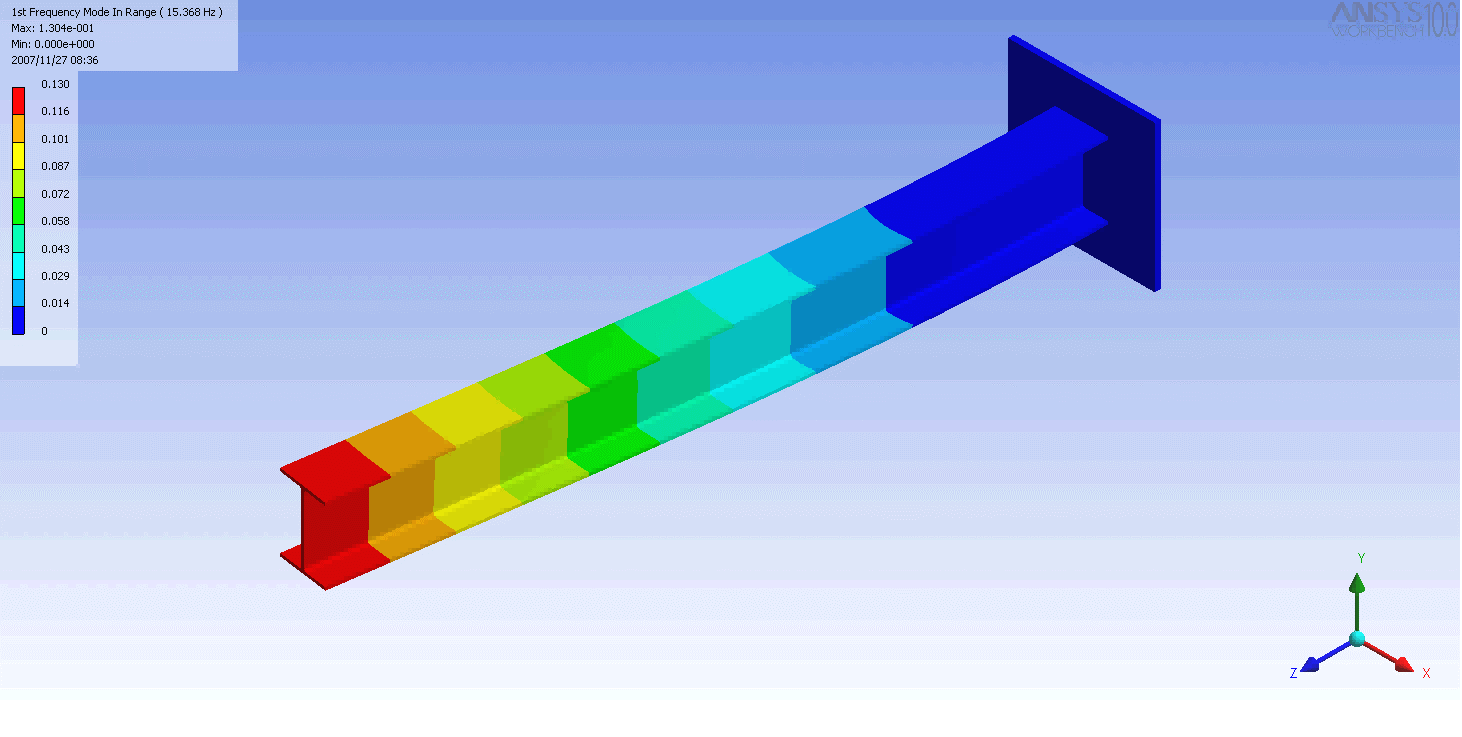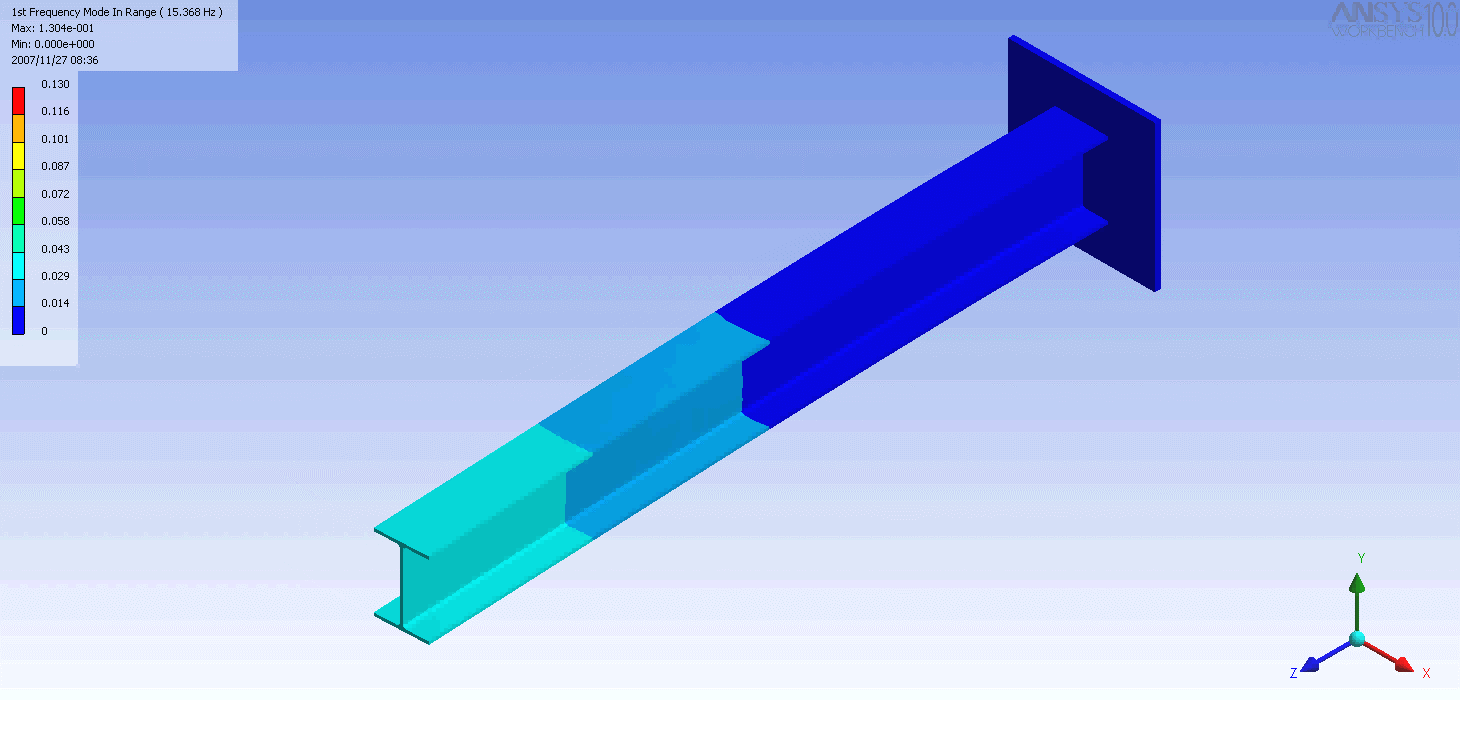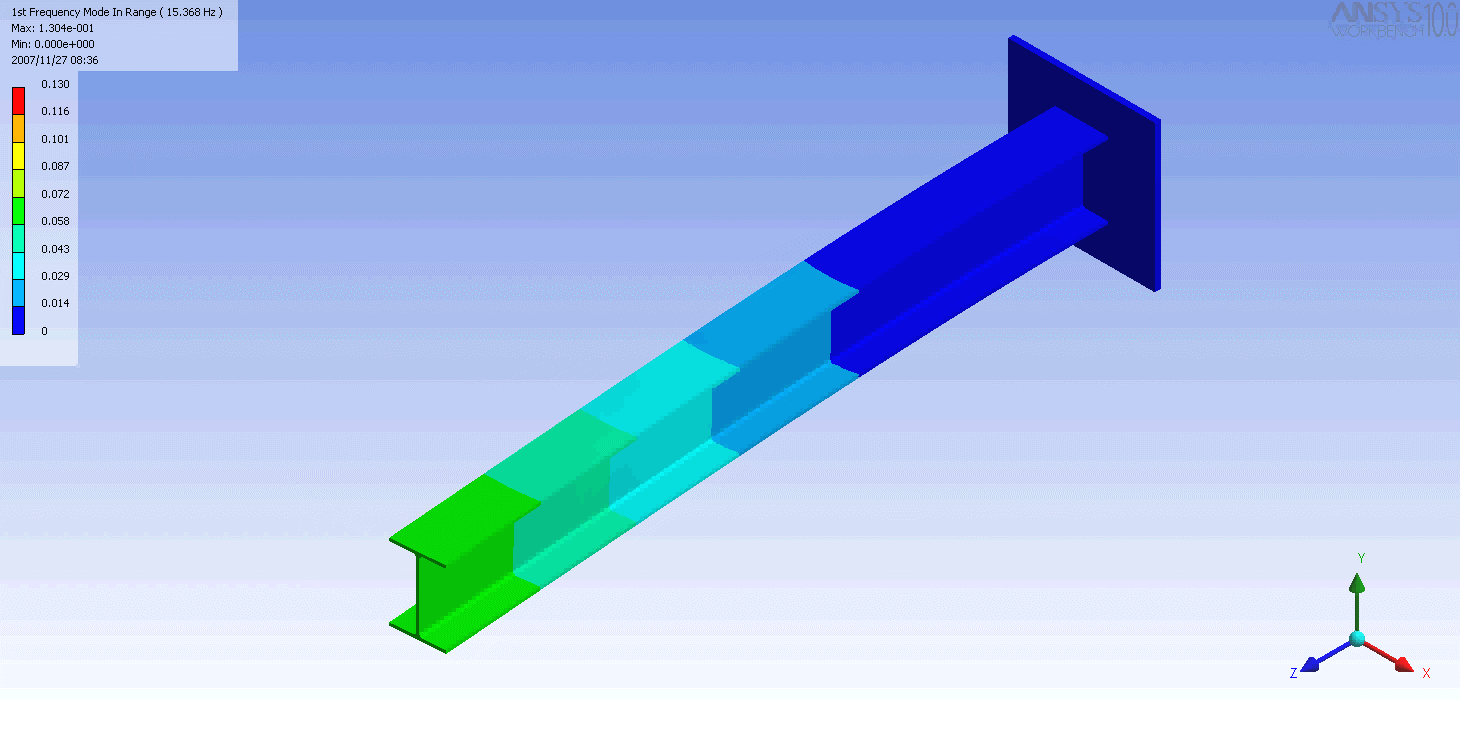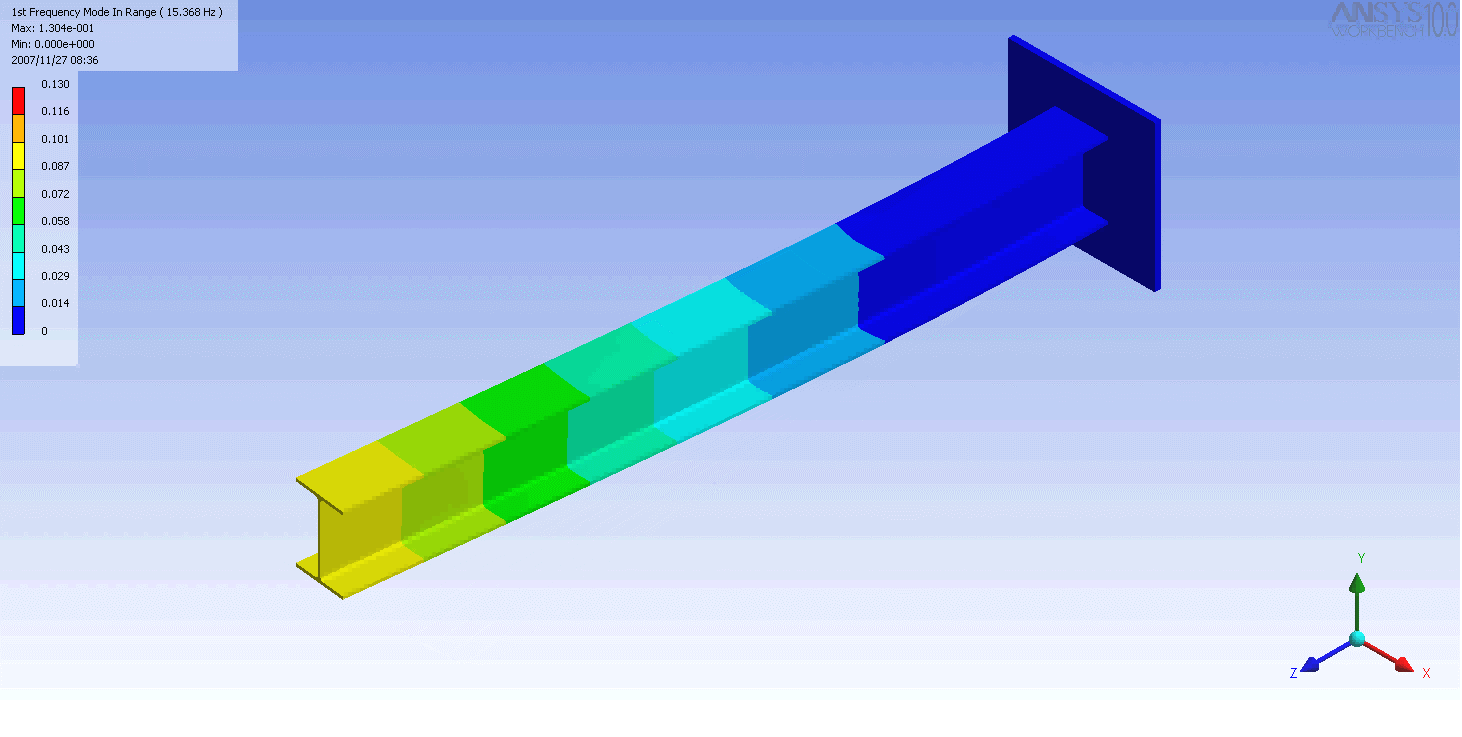
ed I-beam
. In this case, a finite element
model was used to generate the mass and stiffness matrices and solve the eigenvalue problem. Even this relatively simple model has over 100 degrees of freedom and hence as many natural frequencies and mode shapes. In general only the first few modes are important.


 and
and  are diagonal matrices
are diagonal matrices
that contain the modal mass and stiffness values for each one of the modes. (Note: Since the eigenvectors (mode shapes) can be arbitrarily scaled, the orthogonality properties are often used to scale the eigenvectors so the modal mass value for each mode is equal to 1. The modal mass matrix is therefore an identity matrix
)
These properties can be used to greatly simplify the solution of multi-degree of freedom models by making the following coordinate transformation.

If we use this coordinate transformation in our original free vibration differential equation we get the following equation.

We can take advantage of the orthogonality properties by premultiplying this equation by

The orthogonality properties then simplify this equation to:

This equation is the foundation of vibration analysis for multiple degree of freedom systems. A similar type of result can be derived for damped systems. The key is that the modal and stiffness matrices are diagonal matrices and therefore we have "decoupled" the equations. In other words, we have transformed our problem from a large unwieldy multiple degree of freedom problem into many single degree of freedom problems that can be solved using the same methods outlined above.
Instead of solving for x we are instead solving for q, referred to as the modal coordinates or modal participation factors.
It may be clearer to understand if we write as:
as:

Written in this form we can see that the vibration at each of the degrees of freedom is just a linear sum of the mode shapes. Furthermore, how much each mode "participates" in the final vibration is defined by q, its modal participation factor.
such as the motion of a pendulum or random such as the movement of a tire on a gravel road.
Vibration is occasionally "desirable". For example the motion of a tuning fork
, the reed in a woodwind instrument
or harmonica
, or the cone of a loudspeaker
is desirable vibration, necessary for the correct functioning of the various devices.
More often, vibration is undesirable, wasting energy
and creating unwanted sound
– noise
. For example, the vibrational motions of engine
s, electric motor
s, or any mechanical device
in operation are typically unwanted. Such vibrations can be caused by imbalances
in the rotating parts, uneven friction
, the meshing of gear
teeth, etc. Careful designs usually minimize unwanted vibrations.
The study of sound and vibration are closely related. Sound, or "pressure wave
s", are generated by vibrating structures (e.g. vocal cords); these pressure waves can also induce the vibration of structures (e.g. ear drum). Hence, when trying to reduce noise it is often a problem in trying to reduce vibration.


" and damp down to zero.
Forced vibration is when an alternating force or motion is applied to a mechanical system. Examples of this type of vibration include a shaking washing machine due to an imbalance, transportation vibration (caused by truck engine, springs, road, etc.), or the vibration of a building during an earthquake
. In forced vibration the frequency of the vibration is the frequency of the force or motion applied, with order of magnitude being dependent on the actual mechanical system.
Two typical types of vibration tests performed are random- and sine test. Sine (one-frequency-at-a-time) tests are performed to survey the structural response of the device under test (DUT). A random (all frequencies at once) test is generally considered to more closely replicate a real world environment, such as road inputs to a moving automobile.
Most vibration testing is conducted in a single DUT axis at a time, even though most real-world vibration occurs in various axes simultaneously. MIL-STD-810G, released in late 2008, Test Method 527, calls for multiple exciter testing.
–spring
–damper
model. Indeed, even a complex structure such as an automobile body can be modeled as a "summation" of simple mass–spring–damper models. The mass–spring–damper model is an example of a simple harmonic oscillator. The mathematics used to describe its behavior is identical to other simple harmonic oscillators such as the RLC circuit
.
Note: In this article the step by step mathematical derivations will not be included, but will focus on the major equations and concepts in vibration analysis. Please refer to the references at the end of the article for detailed derivations.
 To start the investigation of the mass–spring–damper we will assume the damping is negligible and that there is no external force applied to the mass (i.e. free vibration).
To start the investigation of the mass–spring–damper we will assume the damping is negligible and that there is no external force applied to the mass (i.e. free vibration).
The force applied to the mass by the spring is proportional to the amount the spring is stretched "x" (we will assume the spring is already compressed due to the weight of the mass). The proportionality constant, k, is the stiffness of the spring and has units of force/distance (e.g. lbf/in or N/m). The negative sign indicates that the force is always opposing the motion of the mass attached to it.

The force generated by the mass is proportional to the acceleration of the mass as given by Newton’s second law of motion
.

The sum of the forces on the mass then generates this ordinary differential equation
:

 If we assume that we start the system to vibrate by stretching the spring by the distance of A and letting go, the solution to the above equation that describes the motion of mass is:
If we assume that we start the system to vibrate by stretching the spring by the distance of A and letting go, the solution to the above equation that describes the motion of mass is:

This solution says that it will oscillate with simple harmonic motion
that has an amplitude
of A and a frequency of The number
The number  is one of the most important quantities in vibration analysis and is called the undamped natural frequency. For the simple mass–spring system,
is one of the most important quantities in vibration analysis and is called the undamped natural frequency. For the simple mass–spring system,  is defined as:
is defined as:

Note: Angular frequency
 (
( ) with the units of radians per second is often used in equations because it simplifies the equations, but is normally converted to “standard” frequency (units of Hz
) with the units of radians per second is often used in equations because it simplifies the equations, but is normally converted to “standard” frequency (units of Hz
or equivalently cycles per second) when stating the frequency of a system.
If you know the mass and stiffness of the system you can determine the frequency at which the system will vibrate once it is set in motion by an initial disturbance using the above stated formula. Every vibrating system has one or more natural frequencies that it will vibrate at once it is disturbed. This simple relation can be used to understand in general what will happen to a more complex system once we add mass or stiffness. For example, the above formula explains why when a car or truck is fully loaded the suspension will feel “softer” than unloaded because the mass has increased and therefore reduced the natural frequency of the system.
. In the above example we have extended the spring by a value of and therefore have stored some potential energy
and therefore have stored some potential energy
( ) in the spring. Once we let go of the spring, the spring tries to return to its un-stretched state (which is the minimum potential energy state) and in the process accelerates the mass. At the point where the spring has reached its un-stretched state all the potential energy that we supplied by stretching it has been transformed into kinetic energy
) in the spring. Once we let go of the spring, the spring tries to return to its un-stretched state (which is the minimum potential energy state) and in the process accelerates the mass. At the point where the spring has reached its un-stretched state all the potential energy that we supplied by stretching it has been transformed into kinetic energy
( ). The mass then begins to decelerate because it is now compressing the spring and in the process transferring the kinetic energy back to its potential. Thus oscillation of the spring amounts to the transferring back and forth of the kinetic energy into potential energy.
). The mass then begins to decelerate because it is now compressing the spring and in the process transferring the kinetic energy back to its potential. Thus oscillation of the spring amounts to the transferring back and forth of the kinetic energy into potential energy.
In our simple model the mass will continue to oscillate forever at the same magnitude, but in a real system there is always something called damping that dissipates the energy, eventually bringing it to rest.
 We now add a "viscous" damper to the model that outputs a force that is proportional to the velocity of the mass. The damping is called viscous because it models the effects of an object within a fluid. The proportionality constant c is called the damping coefficient and has units of Force over velocity (lbf s/ in or N s/m).
We now add a "viscous" damper to the model that outputs a force that is proportional to the velocity of the mass. The damping is called viscous because it models the effects of an object within a fluid. The proportionality constant c is called the damping coefficient and has units of Force over velocity (lbf s/ in or N s/m).

By summing the forces on the mass we get the following ordinary differential equation:

The solution to this equation depends on the amount of damping. If the damping is small enough the system will still vibrate, but eventually, over time, will stop vibrating. This case is called underdamping – this case is of most interest in vibration analysis. If we increase the damping just to the point where the system no longer oscillates we reach the point of critical damping (if the damping is increased past critical damping the system is called overdamped). The value that the damping coefficient needs to reach for critical damping in the mass spring damper model is:

To characterize the amount of damping in a system a ratio called the damping ratio
(also known as damping factor and % critical damping) is used. This damping ratio is just a ratio of the actual damping over the amount of damping required to reach critical damping. The formula for the damping ratio ( ) of the mass spring damper model is:
) of the mass spring damper model is:

For example, metal structures (e.g. airplane fuselage, engine crankshaft) will have damping factors less than 0.05 while automotive suspensions in the range of 0.2–0.3.
The solution to the underdamped system for the mass spring damper model is the following:

 The value of X, the initial magnitude, and
The value of X, the initial magnitude, and  the phase shift, are determined by the amount the spring is stretched. The formulas for these values can be found in the references.
the phase shift, are determined by the amount the spring is stretched. The formulas for these values can be found in the references.
The frequency in this case is called the "damped natural frequency", and is related to the undamped natural frequency by the following formula:
and is related to the undamped natural frequency by the following formula:

The damped natural frequency is less than the undamped natural frequency, but for many practical cases the damping ratio is relatively small and hence the difference is negligible. Therefore the damped and undamped description are often dropped when stating the natural frequency (e.g. with 0.1 damping ratio, the damped natural frequency is only 1% less than the undamped).
The plots to the side present how 0.1 and 0.3 damping ratios effect how the system will “ring” down over time. What is often done in practice is to experimentally measure the free vibration after an impact (for example by a hammer) and then determine the natural frequency of the system by measuring the rate of oscillation as well as the damping ratio by measuring the rate of decay. The natural frequency and damping ratio are not only important in free vibration, but also characterize how a system will behave under forced vibration.

If we again sum the forces on the mass we get the following ordinary differential equation:

The steady state
solution of this problem can be written as:

The result states that the mass will oscillate at the same frequency, f, of the applied force, but with a phase shift
The amplitude of the vibration “X” is defined by the following formula.

Where “r” is defined as the ratio of the harmonic force frequency over the undamped natural frequency of the mass–spring–damper model.

The phase shift , is defined by the following formula.
is defined by the following formula.

 The plot of these functions, called "the frequency response of the system", presents one of the most important features in forced vibration. In a lightly damped system when the forcing frequency nears the natural frequency (
The plot of these functions, called "the frequency response of the system", presents one of the most important features in forced vibration. In a lightly damped system when the forcing frequency nears the natural frequency ( ) the amplitude of the vibration can get extremely high. This phenomenon is called resonance
) the amplitude of the vibration can get extremely high. This phenomenon is called resonance
(subsequently the natural frequency of a system is often referred to as the resonant frequency). In rotor bearing systems any rotational speed that excites a resonant frequency is referred to as a critical speed
.
If resonance occurs in a mechanical system it can be very harmful – leading to eventual failure of the system. Consequently, one of the major reasons for vibration analysis is to predict when this type of resonance may occur and then to determine what steps to take to prevent it from occurring. As the amplitude plot shows, adding damping can significantly reduce the magnitude of the vibration. Also, the magnitude can be reduced if the natural frequency can be shifted away from the forcing frequency by changing the stiffness or mass of the system. If the system cannot be changed, perhaps the forcing frequency can be shifted (for example, changing the speed of the machine generating the force).
The following are some other points in regards to the forced vibration shown in the frequency response plots.
The damper, instead of storing energy, dissipates energy. Since the damping force is proportional to the velocity, the more the motion, the more the damper dissipates the energy. Therefore a point will come when the energy dissipated by the damper will equal the energy being fed in by the force. At this point, the system has reached its maximum amplitude and will continue to vibrate at this level as long as the force applied stays the same. If no damping exists, there is nothing to dissipate the energy and therefore theoretically the motion will continue to grow on into infinity.
that takes a signal as a function of time (time domain
) and breaks it down into its harmonic components as a function of frequency (frequency domain
). For example, let us apply a force to the mass–spring–damper model that repeats the following cycle – a force equal to 1 newton for 0.5 second and then no force for 0.5 second. This type of force has the shape of a 1 Hz square wave
.
 The Fourier transform of the square wave generates a frequency spectrum
The Fourier transform of the square wave generates a frequency spectrum
that presents the magnitude of the harmonics that make up the square wave (the phase is also generated, but is typically of less concern and therefore is often not plotted). The Fourier transform can also be used to analyze non-periodic
functions such as transients (e.g. impulses) and random functions. With the advent of the modern computer the Fourier transform is almost always computed using the Fast Fourier Transform
(FFT) computer algorithm in combination with a window function
.
In the case of our square wave force, the first component is actually a constant force of 0.5 newton and is represented by a value at "0" Hz in the frequency spectrum. The next component is a 1 Hz sine wave with an amplitude of 0.64. This is shown by the line at 1 Hz. The remaining components are at odd frequencies and it takes an infinite amount of sine waves to generate the perfect square wave. Hence, the Fourier transform allows you to interpret the force as a sum of sinusoidal forces being applied instead of a more "complex" force (e.g. a square wave).
In the previous section, the vibration solution was given for a single harmonic force, but the Fourier transform will in general give multiple harmonic forces. The second mathematical tool, "the principle of superposition"
, allows you to sum the solutions from multiple forces if the system is linear
. In the case of the spring–mass–damper model, the system is linear if the spring force is proportional to the displacement and the damping is proportional to the velocity over the range of motion of interest. Hence, the solution to the problem with a square wave is summing the predicted vibration from each one of the harmonic forces found in the frequency spectrum of the square wave.

 is called the frequency response
is called the frequency response
function (also referred to as the transfer function
, but not technically as accurate) and has both a magnitude and phase component (if represented as a complex number
, a real and imaginary component). The magnitude of the frequency response function (FRF) was presented earlier for the mass–spring–damper system.
 where
where 
The phase of the FRF was also presented earlier as:

For example, let us calculate the FRF for a mass–spring–damper system with a mass of 1 kg, spring stiffness of 1.93 N/mm and a damping ratio of 0.1. The values of the spring and mass give a natural frequency of 7 Hz for this specific system. If we apply the 1 Hz square wave from earlier we can calculate the predicted vibration of the mass. The figure illustrates the resulting vibration. It happens in this example that the fourth harmonic of the square wave falls at 7 Hz. The frequency response of the mass–spring–damper therefore outputs a high 7 Hz vibration even though the input force had a relatively low 7 Hz harmonic. This example highlights that the resulting vibration is dependent on both the forcing function and the system that the force is applied to.
 The figure also shows the time domain representation of the resulting vibration. This is done by performing an inverse Fourier Transform that converts frequency domain data to time domain. In practice, this is rarely done because the frequency spectrum provides all the necessary information.
The figure also shows the time domain representation of the resulting vibration. This is done by performing an inverse Fourier Transform that converts frequency domain data to time domain. In practice, this is rarely done because the frequency spectrum provides all the necessary information.
The frequency response function (FRF) does not necessarily have to be calculated from the knowledge of the mass, damping, and stiffness of the system, but can be measured experimentally. For example, if you apply a known force and sweep the frequency and then measure the resulting vibration you can calculate the frequency response function and then characterize the system. This technique is used in the field of experimental modal analysis
to determine the vibration characteristics of a structure.
(SDOF) model since we have assumed the mass only moves up and down. In the case of more complex systems we need to discretize the system into more masses and allow them to move in more than one direction – adding degrees of freedom. The major concepts of multiple degrees of freedom (MDOF) can be understood by looking at just a 2 degree of freedom model as shown in the figure.
 The equations of motion of the 2DOF system are found to be:
The equations of motion of the 2DOF system are found to be:


We can rewrite this in matrix
format:

A more compact form of this matrix equation can be written as:

where
 and
and  are symmetric matrices referred respectively as the mass, damping, and stiffness matrices. The matrices are NxN square matrices where N is the number of degrees of freedom of the system.
are symmetric matrices referred respectively as the mass, damping, and stiffness matrices. The matrices are NxN square matrices where N is the number of degrees of freedom of the system.
In the following analysis we will consider the case where there is no damping and no applied forces (i.e. free vibration). The solution of a viscously damped system is somewhat more complicated.

This differential equation can be solved by assuming the following type of solution:

Note: Using the exponential solution of is a mathematical trick used to solve linear differential equations. If we use Euler's formula
is a mathematical trick used to solve linear differential equations. If we use Euler's formula
and take only the real part of the solution it is the same cosine solution for the 1 DOF system. The exponential solution is only used because it easier to manipulate mathematically.
The equation then becomes:

Since cannot equal zero the equation reduces to the following.
cannot equal zero the equation reduces to the following.



and if we let and
and 

The solution to the problem results in N eigenvalues (i.e. ), where N corresponds to the number of degrees of freedom. The eigenvalues provide the natural frequencies of the system. When these eigenvalues are substituted back into the original set of equations, the values of
), where N corresponds to the number of degrees of freedom. The eigenvalues provide the natural frequencies of the system. When these eigenvalues are substituted back into the original set of equations, the values of  that correspond to each eigenvalue are called the eigenvectors. These eigenvectors represent the mode shapes of the system. The solution of an eigenvalue problem can be quite cumbersome (especially for problems with many degrees of freedom), but fortunately most math analysis programs have eigenvalue routines.
that correspond to each eigenvalue are called the eigenvectors. These eigenvectors represent the mode shapes of the system. The solution of an eigenvalue problem can be quite cumbersome (especially for problems with many degrees of freedom), but fortunately most math analysis programs have eigenvalue routines.
The eigenvalues and eigenvectors are often written in the following matrix format and describe the modal model of the system:
 and
and 
A simple example using our 2 DOF model can help illustrate the concepts. Let both masses have a mass of 1 kg and the stiffness of all three springs equal 1000 N/m. The mass and stiffness matrix for this problem are then:
 and
and 
Then
The eigenvalues for this problem given by an eigenvalue routine will be:

The natural frequencies in the units of hertz are then (remembering )
)  and
and  .
.
The two mode shapes for the respective natural frequencies are given as:

Since the system is a 2 DOF system, there are two modes with their respective natural frequencies and shapes. The mode shape vectors are not the absolute motion, but just describe relative motion of the degrees of freedom. In our case the first mode shape vector is saying that the masses are moving together in phase since they have the same value and sign. In the case of the second mode shape vector, each mass is moving in opposite direction at the same rate.
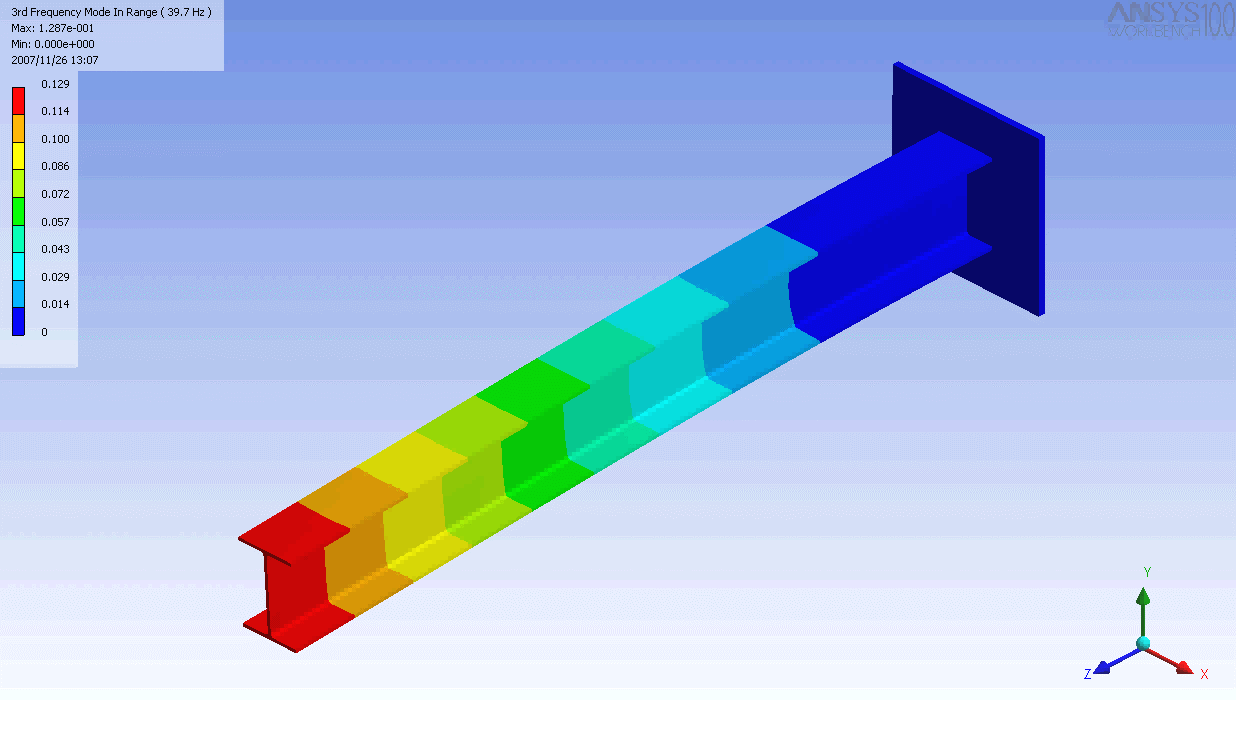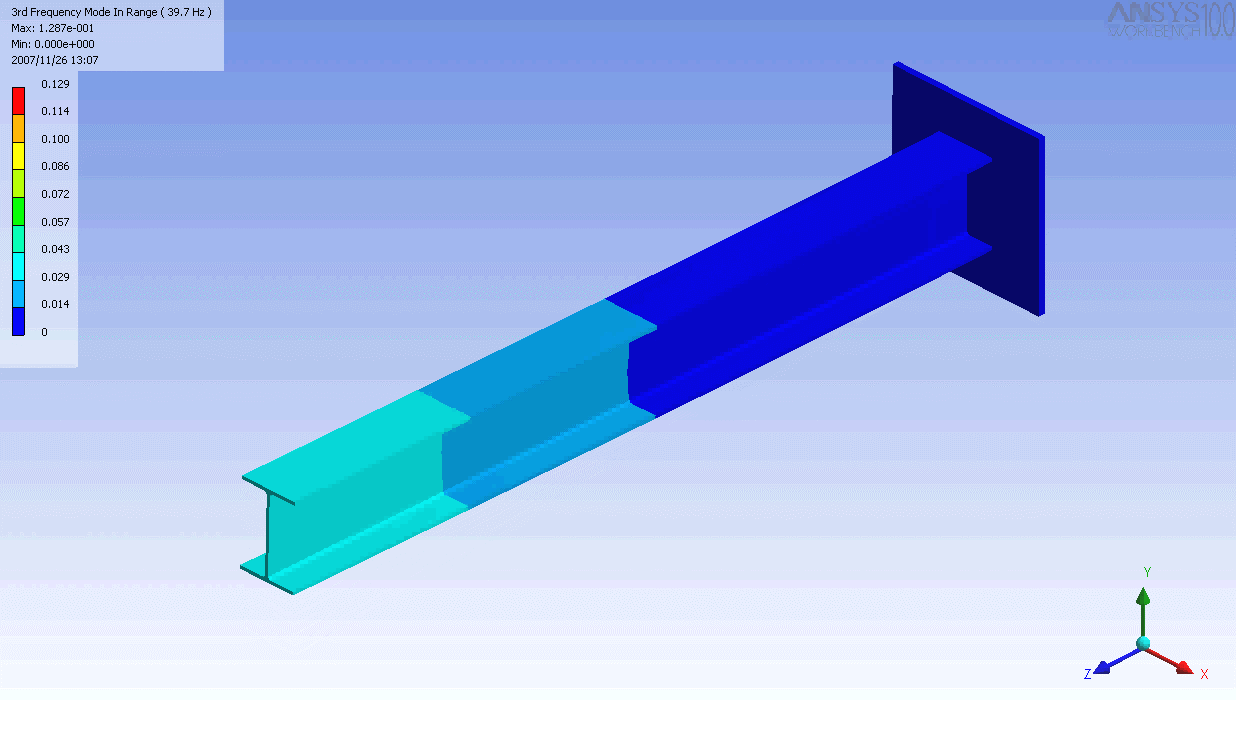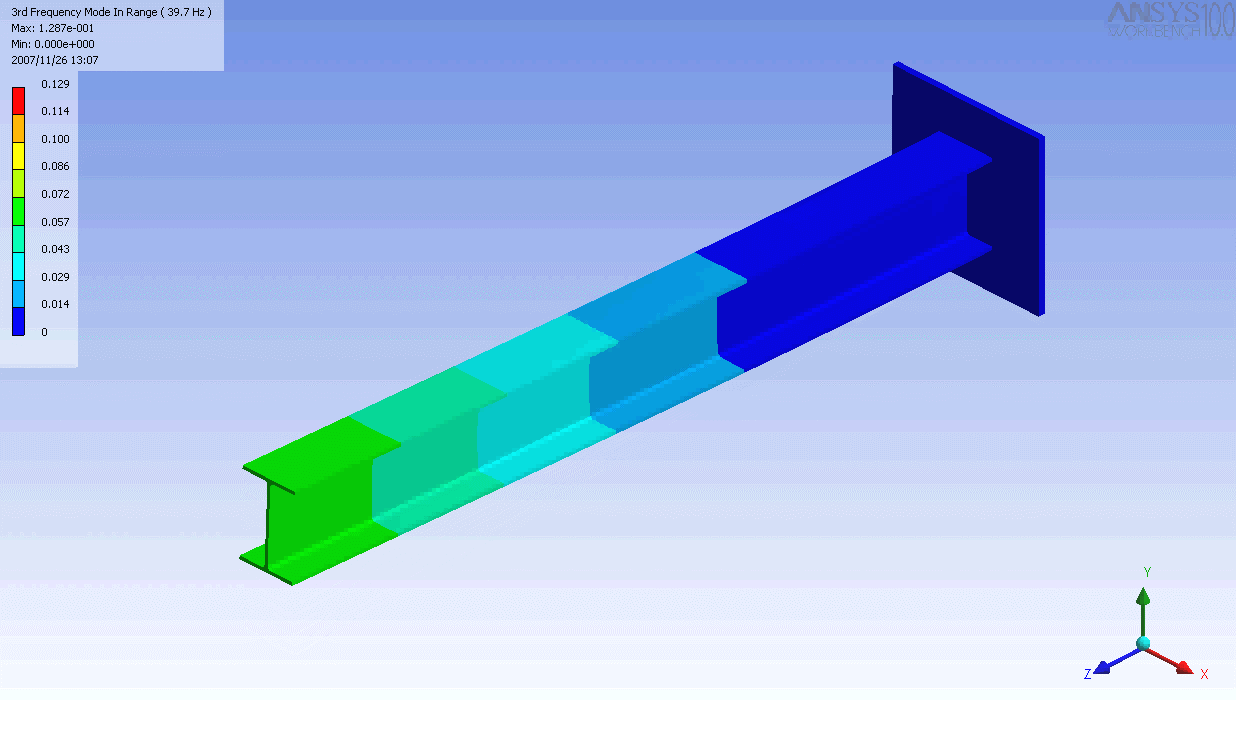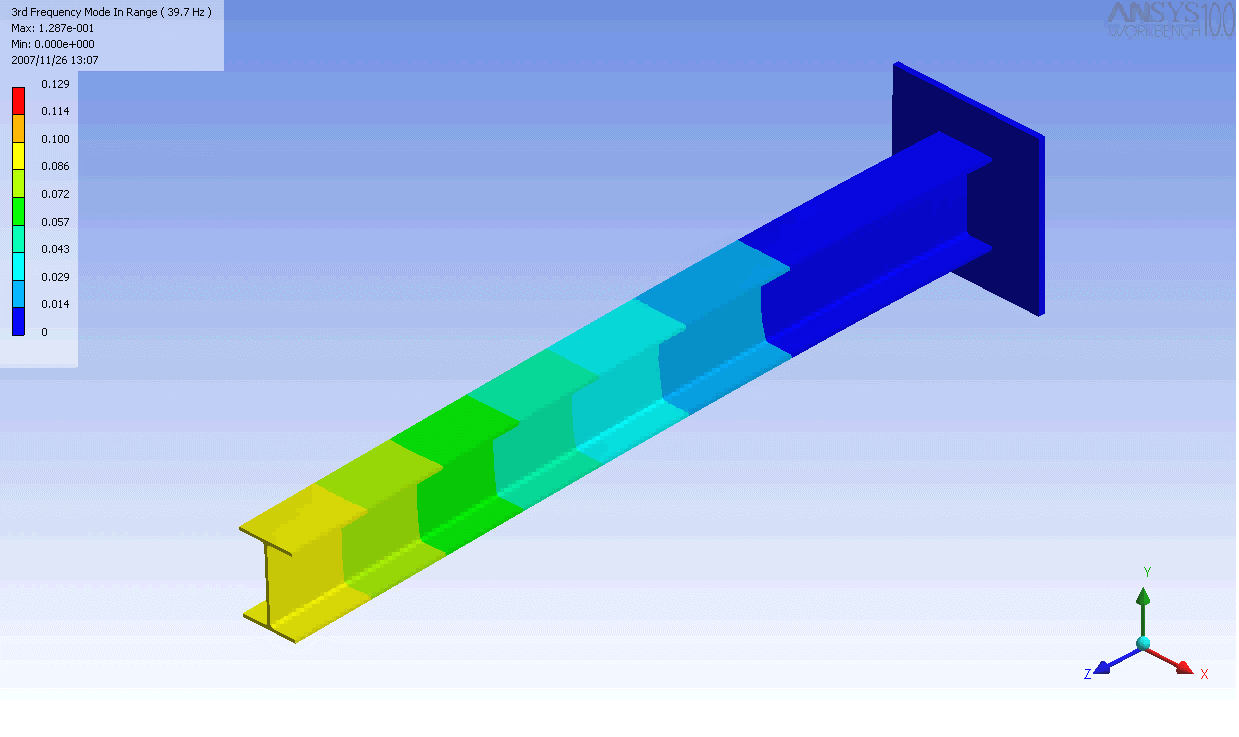
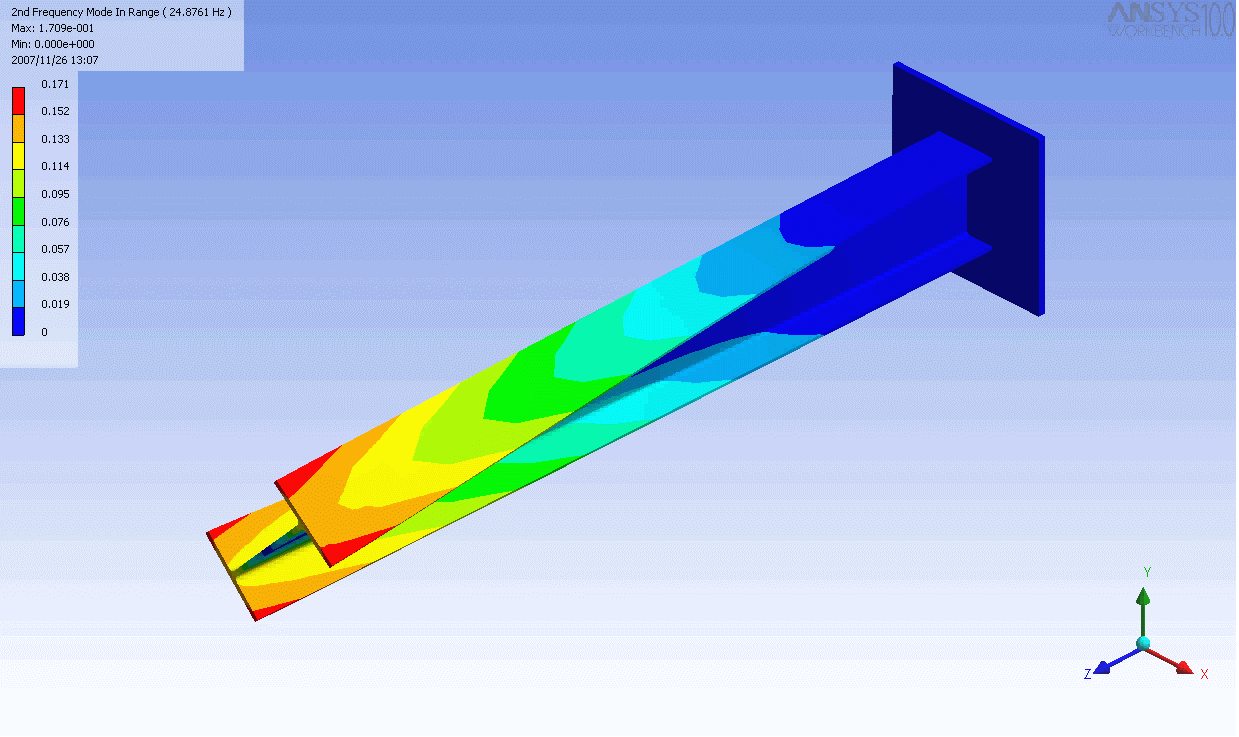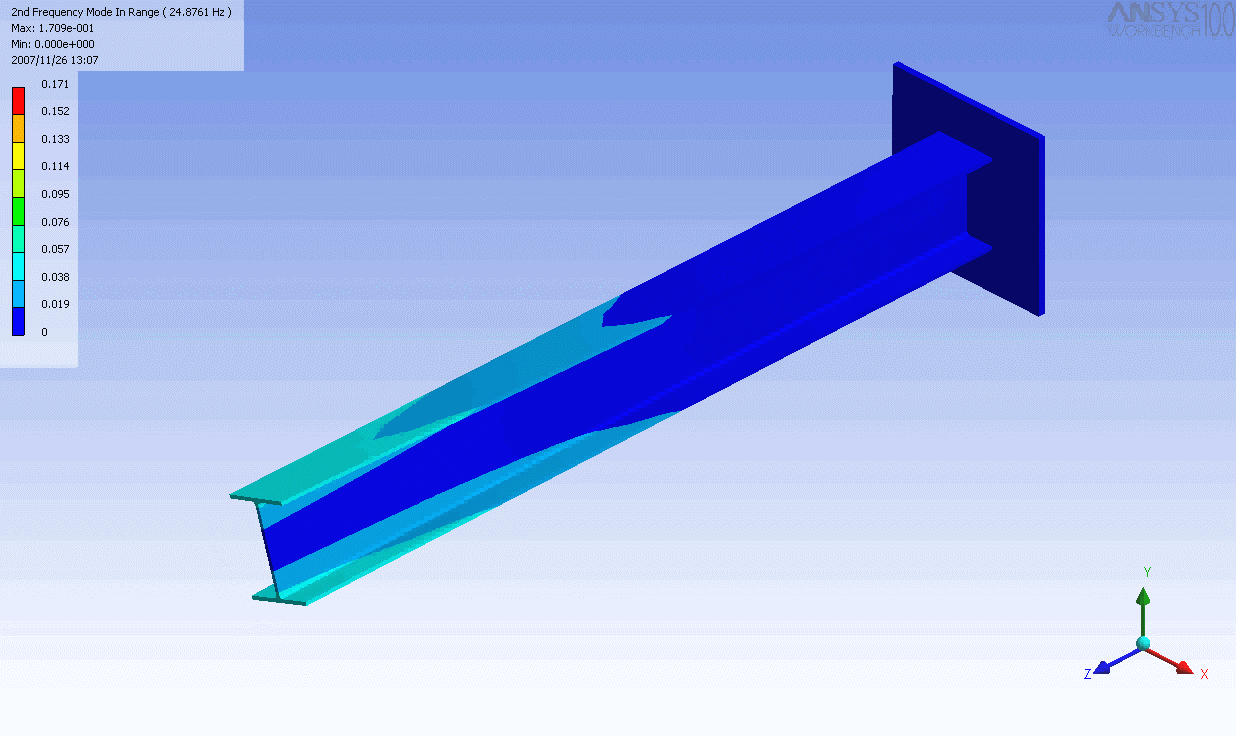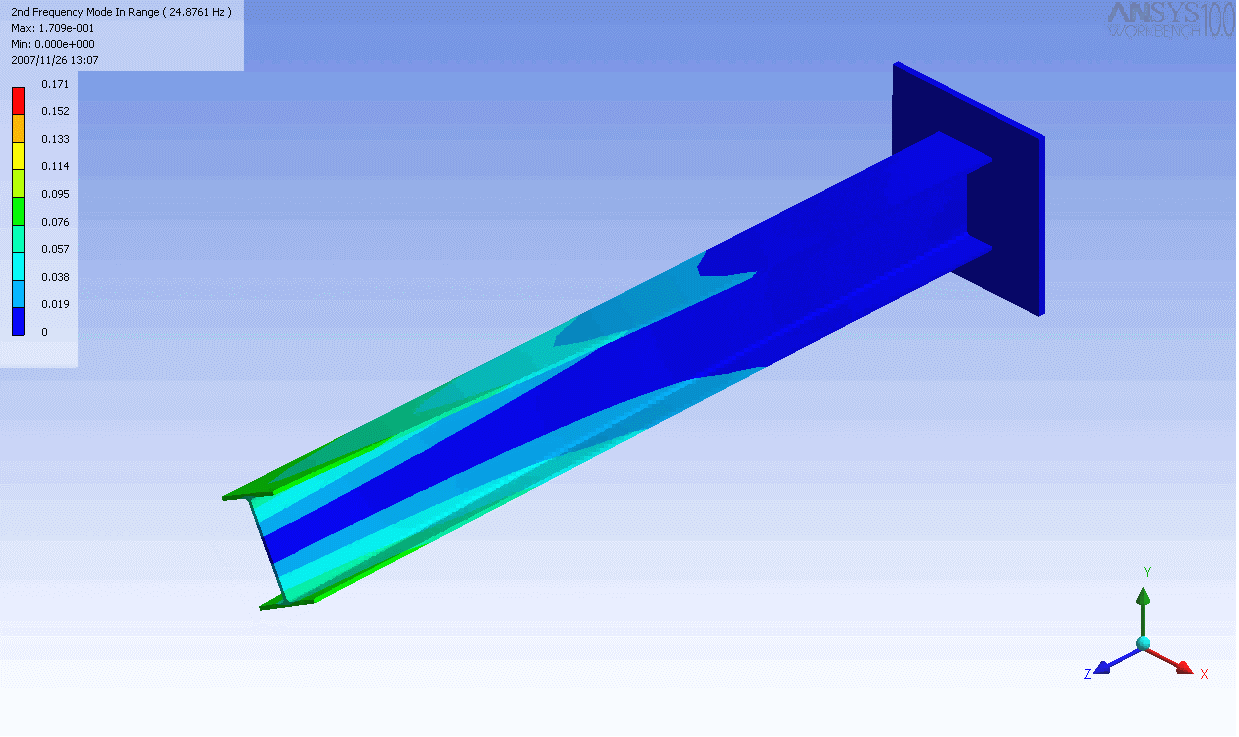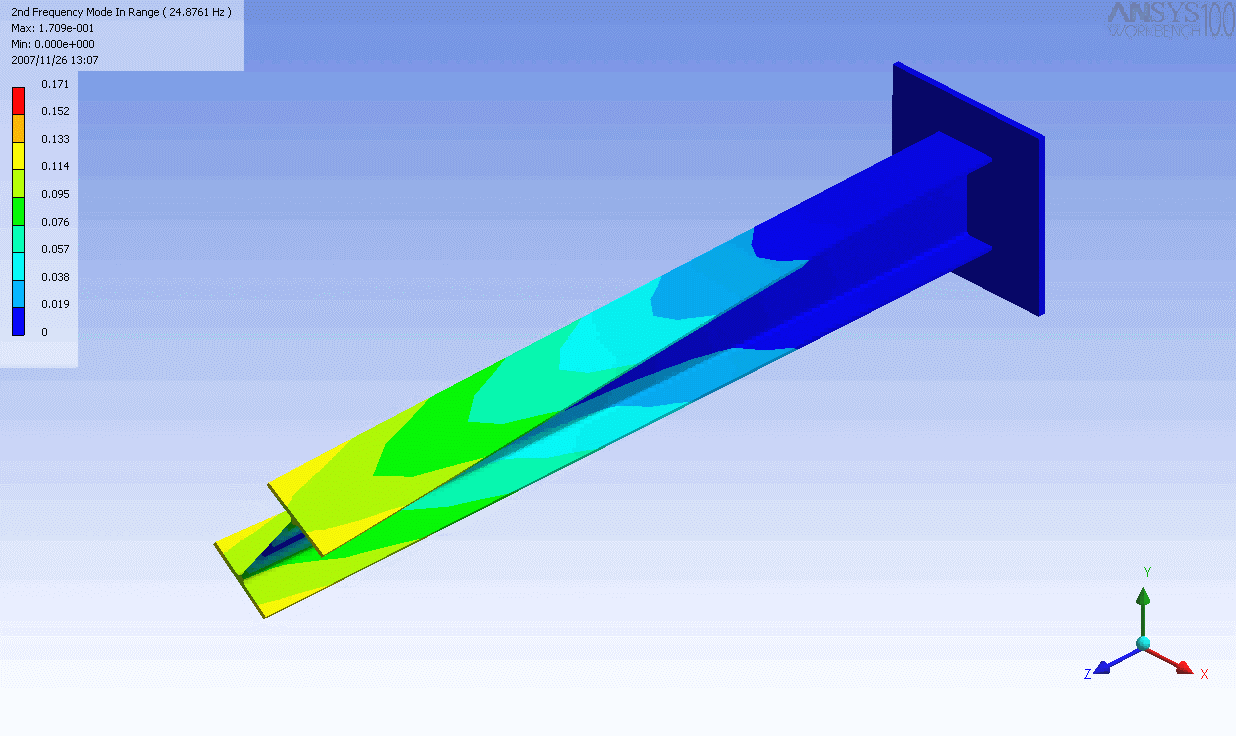
ed I-beam
. In this case, a finite element
model was used to generate the mass and stiffness matrices and solve the eigenvalue problem. Even this relatively simple model has over 100 degrees of freedom and hence as many natural frequencies and mode shapes. In general only the first few modes are important.


 and
and  are diagonal matrices
are diagonal matrices
that contain the modal mass and stiffness values for each one of the modes. (Note: Since the eigenvectors (mode shapes) can be arbitrarily scaled, the orthogonality properties are often used to scale the eigenvectors so the modal mass value for each mode is equal to 1. The modal mass matrix is therefore an identity matrix
)
These properties can be used to greatly simplify the solution of multi-degree of freedom models by making the following coordinate transformation.

If we use this coordinate transformation in our original free vibration differential equation we get the following equation.

We can take advantage of the orthogonality properties by premultiplying this equation by

The orthogonality properties then simplify this equation to:

This equation is the foundation of vibration analysis for multiple degree of freedom systems. A similar type of result can be derived for damped systems. The key is that the modal and stiffness matrices are diagonal matrices and therefore we have "decoupled" the equations. In other words, we have transformed our problem from a large unwieldy multiple degree of freedom problem into many single degree of freedom problems that can be solved using the same methods outlined above.
Instead of solving for x we are instead solving for q, referred to as the modal coordinates or modal participation factors.
It may be clearer to understand if we write as:
as:

Written in this form we can see that the vibration at each of the degrees of freedom is just a linear sum of the mode shapes. Furthermore, how much each mode "participates" in the final vibration is defined by q, its modal participation factor.
such as the motion of a pendulum or random such as the movement of a tire on a gravel road.
Vibration is occasionally "desirable". For example the motion of a tuning fork
, the reed in a woodwind instrument
or harmonica
, or the cone of a loudspeaker
is desirable vibration, necessary for the correct functioning of the various devices.
More often, vibration is undesirable, wasting energy
and creating unwanted sound
– noise
. For example, the vibrational motions of engine
s, electric motor
s, or any mechanical device
in operation are typically unwanted. Such vibrations can be caused by imbalances
in the rotating parts, uneven friction
, the meshing of gear
teeth, etc. Careful designs usually minimize unwanted vibrations.
The study of sound and vibration are closely related. Sound, or "pressure wave
s", are generated by vibrating structures (e.g. vocal cords); these pressure waves can also induce the vibration of structures (e.g. ear drum). Hence, when trying to reduce noise it is often a problem in trying to reduce vibration.


" and damp down to zero.
Forced vibration is when an alternating force or motion is applied to a mechanical system. Examples of this type of vibration include a shaking washing machine due to an imbalance, transportation vibration (caused by truck engine, springs, road, etc.), or the vibration of a building during an earthquake
. In forced vibration the frequency of the vibration is the frequency of the force or motion applied, with order of magnitude being dependent on the actual mechanical system.
Two typical types of vibration tests performed are random- and sine test. Sine (one-frequency-at-a-time) tests are performed to survey the structural response of the device under test (DUT). A random (all frequencies at once) test is generally considered to more closely replicate a real world environment, such as road inputs to a moving automobile.
Most vibration testing is conducted in a single DUT axis at a time, even though most real-world vibration occurs in various axes simultaneously. MIL-STD-810G, released in late 2008, Test Method 527, calls for multiple exciter testing.
–spring
–damper
model. Indeed, even a complex structure such as an automobile body can be modeled as a "summation" of simple mass–spring–damper models. The mass–spring–damper model is an example of a simple harmonic oscillator. The mathematics used to describe its behavior is identical to other simple harmonic oscillators such as the RLC circuit
.
Note: In this article the step by step mathematical derivations will not be included, but will focus on the major equations and concepts in vibration analysis. Please refer to the references at the end of the article for detailed derivations.
 To start the investigation of the mass–spring–damper we will assume the damping is negligible and that there is no external force applied to the mass (i.e. free vibration).
To start the investigation of the mass–spring–damper we will assume the damping is negligible and that there is no external force applied to the mass (i.e. free vibration).
The force applied to the mass by the spring is proportional to the amount the spring is stretched "x" (we will assume the spring is already compressed due to the weight of the mass). The proportionality constant, k, is the stiffness of the spring and has units of force/distance (e.g. lbf/in or N/m). The negative sign indicates that the force is always opposing the motion of the mass attached to it.

The force generated by the mass is proportional to the acceleration of the mass as given by Newton’s second law of motion
.

The sum of the forces on the mass then generates this ordinary differential equation
:

 If we assume that we start the system to vibrate by stretching the spring by the distance of A and letting go, the solution to the above equation that describes the motion of mass is:
If we assume that we start the system to vibrate by stretching the spring by the distance of A and letting go, the solution to the above equation that describes the motion of mass is:

This solution says that it will oscillate with simple harmonic motion
that has an amplitude
of A and a frequency of The number
The number  is one of the most important quantities in vibration analysis and is called the undamped natural frequency. For the simple mass–spring system,
is one of the most important quantities in vibration analysis and is called the undamped natural frequency. For the simple mass–spring system,  is defined as:
is defined as:

Note: Angular frequency
 (
( ) with the units of radians per second is often used in equations because it simplifies the equations, but is normally converted to “standard” frequency (units of Hz
) with the units of radians per second is often used in equations because it simplifies the equations, but is normally converted to “standard” frequency (units of Hz
or equivalently cycles per second) when stating the frequency of a system.
If you know the mass and stiffness of the system you can determine the frequency at which the system will vibrate once it is set in motion by an initial disturbance using the above stated formula. Every vibrating system has one or more natural frequencies that it will vibrate at once it is disturbed. This simple relation can be used to understand in general what will happen to a more complex system once we add mass or stiffness. For example, the above formula explains why when a car or truck is fully loaded the suspension will feel “softer” than unloaded because the mass has increased and therefore reduced the natural frequency of the system.
. In the above example we have extended the spring by a value of and therefore have stored some potential energy
and therefore have stored some potential energy
( ) in the spring. Once we let go of the spring, the spring tries to return to its un-stretched state (which is the minimum potential energy state) and in the process accelerates the mass. At the point where the spring has reached its un-stretched state all the potential energy that we supplied by stretching it has been transformed into kinetic energy
) in the spring. Once we let go of the spring, the spring tries to return to its un-stretched state (which is the minimum potential energy state) and in the process accelerates the mass. At the point where the spring has reached its un-stretched state all the potential energy that we supplied by stretching it has been transformed into kinetic energy
( ). The mass then begins to decelerate because it is now compressing the spring and in the process transferring the kinetic energy back to its potential. Thus oscillation of the spring amounts to the transferring back and forth of the kinetic energy into potential energy.
). The mass then begins to decelerate because it is now compressing the spring and in the process transferring the kinetic energy back to its potential. Thus oscillation of the spring amounts to the transferring back and forth of the kinetic energy into potential energy.
In our simple model the mass will continue to oscillate forever at the same magnitude, but in a real system there is always something called damping that dissipates the energy, eventually bringing it to rest.
 We now add a "viscous" damper to the model that outputs a force that is proportional to the velocity of the mass. The damping is called viscous because it models the effects of an object within a fluid. The proportionality constant c is called the damping coefficient and has units of Force over velocity (lbf s/ in or N s/m).
We now add a "viscous" damper to the model that outputs a force that is proportional to the velocity of the mass. The damping is called viscous because it models the effects of an object within a fluid. The proportionality constant c is called the damping coefficient and has units of Force over velocity (lbf s/ in or N s/m).

By summing the forces on the mass we get the following ordinary differential equation:

The solution to this equation depends on the amount of damping. If the damping is small enough the system will still vibrate, but eventually, over time, will stop vibrating. This case is called underdamping – this case is of most interest in vibration analysis. If we increase the damping just to the point where the system no longer oscillates we reach the point of critical damping (if the damping is increased past critical damping the system is called overdamped). The value that the damping coefficient needs to reach for critical damping in the mass spring damper model is:

To characterize the amount of damping in a system a ratio called the damping ratio
(also known as damping factor and % critical damping) is used. This damping ratio is just a ratio of the actual damping over the amount of damping required to reach critical damping. The formula for the damping ratio ( ) of the mass spring damper model is:
) of the mass spring damper model is:

For example, metal structures (e.g. airplane fuselage, engine crankshaft) will have damping factors less than 0.05 while automotive suspensions in the range of 0.2–0.3.
The solution to the underdamped system for the mass spring damper model is the following:

 The value of X, the initial magnitude, and
The value of X, the initial magnitude, and  the phase shift, are determined by the amount the spring is stretched. The formulas for these values can be found in the references.
the phase shift, are determined by the amount the spring is stretched. The formulas for these values can be found in the references.
The frequency in this case is called the "damped natural frequency", and is related to the undamped natural frequency by the following formula:
and is related to the undamped natural frequency by the following formula:

The damped natural frequency is less than the undamped natural frequency, but for many practical cases the damping ratio is relatively small and hence the difference is negligible. Therefore the damped and undamped description are often dropped when stating the natural frequency (e.g. with 0.1 damping ratio, the damped natural frequency is only 1% less than the undamped).
The plots to the side present how 0.1 and 0.3 damping ratios effect how the system will “ring” down over time. What is often done in practice is to experimentally measure the free vibration after an impact (for example by a hammer) and then determine the natural frequency of the system by measuring the rate of oscillation as well as the damping ratio by measuring the rate of decay. The natural frequency and damping ratio are not only important in free vibration, but also characterize how a system will behave under forced vibration.

If we again sum the forces on the mass we get the following ordinary differential equation:

The steady state
solution of this problem can be written as:

The result states that the mass will oscillate at the same frequency, f, of the applied force, but with a phase shift
The amplitude of the vibration “X” is defined by the following formula.

Where “r” is defined as the ratio of the harmonic force frequency over the undamped natural frequency of the mass–spring–damper model.

The phase shift , is defined by the following formula.
is defined by the following formula.

 The plot of these functions, called "the frequency response of the system", presents one of the most important features in forced vibration. In a lightly damped system when the forcing frequency nears the natural frequency (
The plot of these functions, called "the frequency response of the system", presents one of the most important features in forced vibration. In a lightly damped system when the forcing frequency nears the natural frequency ( ) the amplitude of the vibration can get extremely high. This phenomenon is called resonance
) the amplitude of the vibration can get extremely high. This phenomenon is called resonance
(subsequently the natural frequency of a system is often referred to as the resonant frequency). In rotor bearing systems any rotational speed that excites a resonant frequency is referred to as a critical speed
.
If resonance occurs in a mechanical system it can be very harmful – leading to eventual failure of the system. Consequently, one of the major reasons for vibration analysis is to predict when this type of resonance may occur and then to determine what steps to take to prevent it from occurring. As the amplitude plot shows, adding damping can significantly reduce the magnitude of the vibration. Also, the magnitude can be reduced if the natural frequency can be shifted away from the forcing frequency by changing the stiffness or mass of the system. If the system cannot be changed, perhaps the forcing frequency can be shifted (for example, changing the speed of the machine generating the force).
The following are some other points in regards to the forced vibration shown in the frequency response plots.
The damper, instead of storing energy, dissipates energy. Since the damping force is proportional to the velocity, the more the motion, the more the damper dissipates the energy. Therefore a point will come when the energy dissipated by the damper will equal the energy being fed in by the force. At this point, the system has reached its maximum amplitude and will continue to vibrate at this level as long as the force applied stays the same. If no damping exists, there is nothing to dissipate the energy and therefore theoretically the motion will continue to grow on into infinity.
that takes a signal as a function of time (time domain
) and breaks it down into its harmonic components as a function of frequency (frequency domain
). For example, let us apply a force to the mass–spring–damper model that repeats the following cycle – a force equal to 1 newton for 0.5 second and then no force for 0.5 second. This type of force has the shape of a 1 Hz square wave
.
 The Fourier transform of the square wave generates a frequency spectrum
The Fourier transform of the square wave generates a frequency spectrum
that presents the magnitude of the harmonics that make up the square wave (the phase is also generated, but is typically of less concern and therefore is often not plotted). The Fourier transform can also be used to analyze non-periodic
functions such as transients (e.g. impulses) and random functions. With the advent of the modern computer the Fourier transform is almost always computed using the Fast Fourier Transform
(FFT) computer algorithm in combination with a window function
.
In the case of our square wave force, the first component is actually a constant force of 0.5 newton and is represented by a value at "0" Hz in the frequency spectrum. The next component is a 1 Hz sine wave with an amplitude of 0.64. This is shown by the line at 1 Hz. The remaining components are at odd frequencies and it takes an infinite amount of sine waves to generate the perfect square wave. Hence, the Fourier transform allows you to interpret the force as a sum of sinusoidal forces being applied instead of a more "complex" force (e.g. a square wave).
In the previous section, the vibration solution was given for a single harmonic force, but the Fourier transform will in general give multiple harmonic forces. The second mathematical tool, "the principle of superposition"
, allows you to sum the solutions from multiple forces if the system is linear
. In the case of the spring–mass–damper model, the system is linear if the spring force is proportional to the displacement and the damping is proportional to the velocity over the range of motion of interest. Hence, the solution to the problem with a square wave is summing the predicted vibration from each one of the harmonic forces found in the frequency spectrum of the square wave.

 is called the frequency response
is called the frequency response
function (also referred to as the transfer function
, but not technically as accurate) and has both a magnitude and phase component (if represented as a complex number
, a real and imaginary component). The magnitude of the frequency response function (FRF) was presented earlier for the mass–spring–damper system.
 where
where 
The phase of the FRF was also presented earlier as:

For example, let us calculate the FRF for a mass–spring–damper system with a mass of 1 kg, spring stiffness of 1.93 N/mm and a damping ratio of 0.1. The values of the spring and mass give a natural frequency of 7 Hz for this specific system. If we apply the 1 Hz square wave from earlier we can calculate the predicted vibration of the mass. The figure illustrates the resulting vibration. It happens in this example that the fourth harmonic of the square wave falls at 7 Hz. The frequency response of the mass–spring–damper therefore outputs a high 7 Hz vibration even though the input force had a relatively low 7 Hz harmonic. This example highlights that the resulting vibration is dependent on both the forcing function and the system that the force is applied to.
 The figure also shows the time domain representation of the resulting vibration. This is done by performing an inverse Fourier Transform that converts frequency domain data to time domain. In practice, this is rarely done because the frequency spectrum provides all the necessary information.
The figure also shows the time domain representation of the resulting vibration. This is done by performing an inverse Fourier Transform that converts frequency domain data to time domain. In practice, this is rarely done because the frequency spectrum provides all the necessary information.
The frequency response function (FRF) does not necessarily have to be calculated from the knowledge of the mass, damping, and stiffness of the system, but can be measured experimentally. For example, if you apply a known force and sweep the frequency and then measure the resulting vibration you can calculate the frequency response function and then characterize the system. This technique is used in the field of experimental modal analysis
to determine the vibration characteristics of a structure.
(SDOF) model since we have assumed the mass only moves up and down. In the case of more complex systems we need to discretize the system into more masses and allow them to move in more than one direction – adding degrees of freedom. The major concepts of multiple degrees of freedom (MDOF) can be understood by looking at just a 2 degree of freedom model as shown in the figure.
 The equations of motion of the 2DOF system are found to be:
The equations of motion of the 2DOF system are found to be:


We can rewrite this in matrix
format:

A more compact form of this matrix equation can be written as:

where
 and
and  are symmetric matrices referred respectively as the mass, damping, and stiffness matrices. The matrices are NxN square matrices where N is the number of degrees of freedom of the system.
are symmetric matrices referred respectively as the mass, damping, and stiffness matrices. The matrices are NxN square matrices where N is the number of degrees of freedom of the system.
In the following analysis we will consider the case where there is no damping and no applied forces (i.e. free vibration). The solution of a viscously damped system is somewhat more complicated.

This differential equation can be solved by assuming the following type of solution:

Note: Using the exponential solution of is a mathematical trick used to solve linear differential equations. If we use Euler's formula
is a mathematical trick used to solve linear differential equations. If we use Euler's formula
and take only the real part of the solution it is the same cosine solution for the 1 DOF system. The exponential solution is only used because it easier to manipulate mathematically.
The equation then becomes:

Since cannot equal zero the equation reduces to the following.
cannot equal zero the equation reduces to the following.



and if we let and
and 

The solution to the problem results in N eigenvalues (i.e. ), where N corresponds to the number of degrees of freedom. The eigenvalues provide the natural frequencies of the system. When these eigenvalues are substituted back into the original set of equations, the values of
), where N corresponds to the number of degrees of freedom. The eigenvalues provide the natural frequencies of the system. When these eigenvalues are substituted back into the original set of equations, the values of  that correspond to each eigenvalue are called the eigenvectors. These eigenvectors represent the mode shapes of the system. The solution of an eigenvalue problem can be quite cumbersome (especially for problems with many degrees of freedom), but fortunately most math analysis programs have eigenvalue routines.
that correspond to each eigenvalue are called the eigenvectors. These eigenvectors represent the mode shapes of the system. The solution of an eigenvalue problem can be quite cumbersome (especially for problems with many degrees of freedom), but fortunately most math analysis programs have eigenvalue routines.
The eigenvalues and eigenvectors are often written in the following matrix format and describe the modal model of the system:
 and
and 
A simple example using our 2 DOF model can help illustrate the concepts. Let both masses have a mass of 1 kg and the stiffness of all three springs equal 1000 N/m. The mass and stiffness matrix for this problem are then:
 and
and 
Then
The eigenvalues for this problem given by an eigenvalue routine will be:

The natural frequencies in the units of hertz are then (remembering )
)  and
and  .
.
The two mode shapes for the respective natural frequencies are given as:

Since the system is a 2 DOF system, there are two modes with their respective natural frequencies and shapes. The mode shape vectors are not the absolute motion, but just describe relative motion of the degrees of freedom. In our case the first mode shape vector is saying that the masses are moving together in phase since they have the same value and sign. In the case of the second mode shape vector, each mass is moving in opposite direction at the same rate.
ed I-beam
. In this case, a finite element
model was used to generate the mass and stiffness matrices and solve the eigenvalue problem. Even this relatively simple model has over 100 degrees of freedom and hence as many natural frequencies and mode shapes. In general only the first few modes are important.


 and
and  are diagonal matrices
are diagonal matrices
that contain the modal mass and stiffness values for each one of the modes. (Note: Since the eigenvectors (mode shapes) can be arbitrarily scaled, the orthogonality properties are often used to scale the eigenvectors so the modal mass value for each mode is equal to 1. The modal mass matrix is therefore an identity matrix
)
These properties can be used to greatly simplify the solution of multi-degree of freedom models by making the following coordinate transformation.

If we use this coordinate transformation in our original free vibration differential equation we get the following equation.

We can take advantage of the orthogonality properties by premultiplying this equation by

The orthogonality properties then simplify this equation to:

This equation is the foundation of vibration analysis for multiple degree of freedom systems. A similar type of result can be derived for damped systems. The key is that the modal and stiffness matrices are diagonal matrices and therefore we have "decoupled" the equations. In other words, we have transformed our problem from a large unwieldy multiple degree of freedom problem into many single degree of freedom problems that can be solved using the same methods outlined above.
Instead of solving for x we are instead solving for q, referred to as the modal coordinates or modal participation factors.
It may be clearer to understand if we write as:
as:

Written in this form we can see that the vibration at each of the degrees of freedom is just a linear sum of the mode shapes. Furthermore, how much each mode "participates" in the final vibration is defined by q, its modal participation factor.
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
such as the motion of a pendulum or random such as the movement of a tire on a gravel road.
Vibration is occasionally "desirable". For example the motion of a tuning fork
Tuning fork
A tuning fork is an acoustic resonator in the form of a two-pronged fork with the prongs formed from a U-shaped bar of elastic metal . It resonates at a specific constant pitch when set vibrating by striking it against a surface or with an object, and emits a pure musical tone after waiting a...
, the reed in a woodwind instrument
Woodwind instrument
A woodwind instrument is a musical instrument which produces sound when the player blows air against a sharp edge or through a reed, causing the air within its resonator to vibrate...
or harmonica
Harmonica
The harmonica, also called harp, French harp, blues harp, and mouth organ, is a free reed wind instrument used primarily in blues and American folk music, jazz, country, and rock and roll. It is played by blowing air into it or drawing air out by placing lips over individual holes or multiple holes...
, or the cone of a loudspeaker
Loudspeaker
A loudspeaker is an electroacoustic transducer that produces sound in response to an electrical audio signal input. Non-electrical loudspeakers were developed as accessories to telephone systems, but electronic amplification by vacuum tube made loudspeakers more generally useful...
is desirable vibration, necessary for the correct functioning of the various devices.
More often, vibration is undesirable, wasting energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
and creating unwanted sound
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
– noise
Noise
In common use, the word noise means any unwanted sound. In both analog and digital electronics, noise is random unwanted perturbation to a wanted signal; it is called noise as a generalisation of the acoustic noise heard when listening to a weak radio transmission with significant electrical noise...
. For example, the vibrational motions of engine
Engine
An engine or motor is a machine designed to convert energy into useful mechanical motion. Heat engines, including internal combustion engines and external combustion engines burn a fuel to create heat which is then used to create motion...
s, electric motor
Electric motor
An electric motor converts electrical energy into mechanical energy.Most electric motors operate through the interaction of magnetic fields and current-carrying conductors to generate force...
s, or any mechanical device
Machine
A machine manages power to accomplish a task, examples include, a mechanical system, a computing system, an electronic system, and a molecular machine. In common usage, the meaning is that of a device having parts that perform or assist in performing any type of work...
in operation are typically unwanted. Such vibrations can be caused by imbalances
Engine balance
Engine balance is the design, construction and tuning of an engine to run smoothly. Improving engine balance reduces vibration and other stresses and can improve the overall performance, efficiency, cost of ownership and reliability of the engine, as well as reducing the stress on other machinery...
in the rotating parts, uneven friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
, the meshing of gear
Gear
A gear is a rotating machine part having cut teeth, or cogs, which mesh with another toothed part in order to transmit torque. Two or more gears working in tandem are called a transmission and can produce a mechanical advantage through a gear ratio and thus may be considered a simple machine....
teeth, etc. Careful designs usually minimize unwanted vibrations.
The study of sound and vibration are closely related. Sound, or "pressure wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
s", are generated by vibrating structures (e.g. vocal cords); these pressure waves can also induce the vibration of structures (e.g. ear drum). Hence, when trying to reduce noise it is often a problem in trying to reduce vibration.


Types of vibration
Free vibration occurs when a mechanical system is set off with an initial input and then allowed to vibrate freely. Examples of this type of vibration are pulling a child back on a swing and then letting go or hitting a tuning fork and letting it ring. The mechanical system will then vibrate at one or more of its "natural frequencyResonance
In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...
" and damp down to zero.
Forced vibration is when an alternating force or motion is applied to a mechanical system. Examples of this type of vibration include a shaking washing machine due to an imbalance, transportation vibration (caused by truck engine, springs, road, etc.), or the vibration of a building during an earthquake
Earthquake
An earthquake is the result of a sudden release of energy in the Earth's crust that creates seismic waves. The seismicity, seismism or seismic activity of an area refers to the frequency, type and size of earthquakes experienced over a period of time...
. In forced vibration the frequency of the vibration is the frequency of the force or motion applied, with order of magnitude being dependent on the actual mechanical system.
Vibration testing
Vibration testing is accomplished by introducing a forcing function into a structure, usually with some type of shaker. Alternately, a DUT (device under test) is attached to the "table" of a shaker. For relatively low frequency forcing, servohydraulic (electrohydraulic) shakers are used. For higher frequencies, electrodynamic shakers are used. Generally, one or more "input" or "control" points located on the DUT-side of a fixture is kept at a specified acceleration. Other "response" points experience maximum vibration level (resonance) or minimum vibration level (anti-resonance).Two typical types of vibration tests performed are random- and sine test. Sine (one-frequency-at-a-time) tests are performed to survey the structural response of the device under test (DUT). A random (all frequencies at once) test is generally considered to more closely replicate a real world environment, such as road inputs to a moving automobile.
Most vibration testing is conducted in a single DUT axis at a time, even though most real-world vibration occurs in various axes simultaneously. MIL-STD-810G, released in late 2008, Test Method 527, calls for multiple exciter testing.
Vibration analysis
The fundamentals of vibration analysis can be understood by studying the simple massMass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
–spring
Spring (device)
A spring is an elastic object used to store mechanical energy. Springs are usually made out of spring steel. Small springs can be wound from pre-hardened stock, while larger ones are made from annealed steel and hardened after fabrication...
–damper
Shock absorber
A shock absorber is a mechanical device designed to smooth out or damp shock impulse, and dissipate kinetic energy. It is a type of dashpot.-Nomenclature:...
model. Indeed, even a complex structure such as an automobile body can be modeled as a "summation" of simple mass–spring–damper models. The mass–spring–damper model is an example of a simple harmonic oscillator. The mathematics used to describe its behavior is identical to other simple harmonic oscillators such as the RLC circuit
RLC circuit
An RLC circuit is an electrical circuit consisting of a resistor, an inductor, and a capacitor, connected in series or in parallel. The RLC part of the name is due to those letters being the usual electrical symbols for resistance, inductance and capacitance respectively...
.
Note: In this article the step by step mathematical derivations will not be included, but will focus on the major equations and concepts in vibration analysis. Please refer to the references at the end of the article for detailed derivations.
Free vibration without damping

The force applied to the mass by the spring is proportional to the amount the spring is stretched "x" (we will assume the spring is already compressed due to the weight of the mass). The proportionality constant, k, is the stiffness of the spring and has units of force/distance (e.g. lbf/in or N/m). The negative sign indicates that the force is always opposing the motion of the mass attached to it.

The force generated by the mass is proportional to the acceleration of the mass as given by Newton’s second law of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
.

The sum of the forces on the mass then generates this ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
:



This solution says that it will oscillate with simple harmonic motion
Simple harmonic motion
Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
that has an amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of A and a frequency of
 The number
The number  is one of the most important quantities in vibration analysis and is called the undamped natural frequency. For the simple mass–spring system,
is one of the most important quantities in vibration analysis and is called the undamped natural frequency. For the simple mass–spring system,  is defined as:
is defined as:
Note: Angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
 (
( ) with the units of radians per second is often used in equations because it simplifies the equations, but is normally converted to “standard” frequency (units of Hz
) with the units of radians per second is often used in equations because it simplifies the equations, but is normally converted to “standard” frequency (units of HzHertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
or equivalently cycles per second) when stating the frequency of a system.
If you know the mass and stiffness of the system you can determine the frequency at which the system will vibrate once it is set in motion by an initial disturbance using the above stated formula. Every vibrating system has one or more natural frequencies that it will vibrate at once it is disturbed. This simple relation can be used to understand in general what will happen to a more complex system once we add mass or stiffness. For example, the above formula explains why when a car or truck is fully loaded the suspension will feel “softer” than unloaded because the mass has increased and therefore reduced the natural frequency of the system.
What causes the system to vibrate: from conservation of energy point of view
Vibrational motion could be understood in terms of conservation of energyConservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
. In the above example we have extended the spring by a value of
 and therefore have stored some potential energy
and therefore have stored some potential energyPotential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
(
 ) in the spring. Once we let go of the spring, the spring tries to return to its un-stretched state (which is the minimum potential energy state) and in the process accelerates the mass. At the point where the spring has reached its un-stretched state all the potential energy that we supplied by stretching it has been transformed into kinetic energy
) in the spring. Once we let go of the spring, the spring tries to return to its un-stretched state (which is the minimum potential energy state) and in the process accelerates the mass. At the point where the spring has reached its un-stretched state all the potential energy that we supplied by stretching it has been transformed into kinetic energyKinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
(
 ). The mass then begins to decelerate because it is now compressing the spring and in the process transferring the kinetic energy back to its potential. Thus oscillation of the spring amounts to the transferring back and forth of the kinetic energy into potential energy.
). The mass then begins to decelerate because it is now compressing the spring and in the process transferring the kinetic energy back to its potential. Thus oscillation of the spring amounts to the transferring back and forth of the kinetic energy into potential energy.In our simple model the mass will continue to oscillate forever at the same magnitude, but in a real system there is always something called damping that dissipates the energy, eventually bringing it to rest.
Free vibration with damping


By summing the forces on the mass we get the following ordinary differential equation:

The solution to this equation depends on the amount of damping. If the damping is small enough the system will still vibrate, but eventually, over time, will stop vibrating. This case is called underdamping – this case is of most interest in vibration analysis. If we increase the damping just to the point where the system no longer oscillates we reach the point of critical damping (if the damping is increased past critical damping the system is called overdamped). The value that the damping coefficient needs to reach for critical damping in the mass spring damper model is:

To characterize the amount of damping in a system a ratio called the damping ratio
Damping ratio
[[Image:Damped spring.gif|right|frame|Underdamped [[spring–mass system]] with ζ 1 , and is referred to as overdamped.*Underdamped:If s is a complex number, then the solution is a decaying exponential combined with an oscillatory portion that looks like \exp...
(also known as damping factor and % critical damping) is used. This damping ratio is just a ratio of the actual damping over the amount of damping required to reach critical damping. The formula for the damping ratio (
 ) of the mass spring damper model is:
) of the mass spring damper model is:
For example, metal structures (e.g. airplane fuselage, engine crankshaft) will have damping factors less than 0.05 while automotive suspensions in the range of 0.2–0.3.
The solution to the underdamped system for the mass spring damper model is the following:


 the phase shift, are determined by the amount the spring is stretched. The formulas for these values can be found in the references.
the phase shift, are determined by the amount the spring is stretched. The formulas for these values can be found in the references.Damped and undamped natural frequencies
The major points to note from the solution are the exponential term and the cosine function. The exponential term defines how quickly the system “damps” down – the larger the damping ratio, the quicker it damps to zero. The cosine function is the oscillating portion of the solution, but the frequency of the oscillations is different from the undamped case.The frequency in this case is called the "damped natural frequency",
 and is related to the undamped natural frequency by the following formula:
and is related to the undamped natural frequency by the following formula:
The damped natural frequency is less than the undamped natural frequency, but for many practical cases the damping ratio is relatively small and hence the difference is negligible. Therefore the damped and undamped description are often dropped when stating the natural frequency (e.g. with 0.1 damping ratio, the damped natural frequency is only 1% less than the undamped).
The plots to the side present how 0.1 and 0.3 damping ratios effect how the system will “ring” down over time. What is often done in practice is to experimentally measure the free vibration after an impact (for example by a hammer) and then determine the natural frequency of the system by measuring the rate of oscillation as well as the damping ratio by measuring the rate of decay. The natural frequency and damping ratio are not only important in free vibration, but also characterize how a system will behave under forced vibration.
Forced vibration with damping
In this section we will see the behavior of the spring mass damper model when we add a harmonic force in the form below. A force of this type could, for example, be generated by a rotating imbalance.
If we again sum the forces on the mass we get the following ordinary differential equation:

The steady state
Steady state
A system in a steady state has numerous properties that are unchanging in time. This implies that for any property p of the system, the partial derivative with respect to time is zero:...
solution of this problem can be written as:

The result states that the mass will oscillate at the same frequency, f, of the applied force, but with a phase shift

The amplitude of the vibration “X” is defined by the following formula.

Where “r” is defined as the ratio of the harmonic force frequency over the undamped natural frequency of the mass–spring–damper model.

The phase shift ,
 is defined by the following formula.
is defined by the following formula.

 ) the amplitude of the vibration can get extremely high. This phenomenon is called resonance
) the amplitude of the vibration can get extremely high. This phenomenon is called resonanceMechanical resonance
Mechanical resonance is the tendency of a mechanical system to absorb more energy when the frequency of its oscillations matches the system's natural frequency of vibration than it does at other frequencies...
(subsequently the natural frequency of a system is often referred to as the resonant frequency). In rotor bearing systems any rotational speed that excites a resonant frequency is referred to as a critical speed
Critical speed
In solid mechanics, in the field of rotordynamics, the critical speed is the theoretical angular velocity which excites the natural frequency of a rotating object, such as a shaft, propeller, leadscrew, or gear. As the speed of rotation approaches the object's natural frequency, the object begins...
.
If resonance occurs in a mechanical system it can be very harmful – leading to eventual failure of the system. Consequently, one of the major reasons for vibration analysis is to predict when this type of resonance may occur and then to determine what steps to take to prevent it from occurring. As the amplitude plot shows, adding damping can significantly reduce the magnitude of the vibration. Also, the magnitude can be reduced if the natural frequency can be shifted away from the forcing frequency by changing the stiffness or mass of the system. If the system cannot be changed, perhaps the forcing frequency can be shifted (for example, changing the speed of the machine generating the force).
The following are some other points in regards to the forced vibration shown in the frequency response plots.
- At a given frequency ratio, the amplitude of the vibration, X, is directly proportional to the amplitude of the force
 (e.g. if you double the force, the vibration doubles)
(e.g. if you double the force, the vibration doubles) - With little or no damping, the vibration is in phase with the forcing frequency when the frequency ratio r < 1 and 180 degrees out of phase when the frequency ratio r > 1
- When r ≪ 1 the amplitude is just the deflection of the spring under the static force
 This deflection is called the static deflection
This deflection is called the static deflection  Hence, when r ≪ 1 the effects of the damper and the mass are minimal.
Hence, when r ≪ 1 the effects of the damper and the mass are minimal. - When r ≫ 1 the amplitude of the vibration is actually less than the static deflection
 In this region the force generated by the mass (F = ma) is dominating because the acceleration seen by the mass increases with the frequency. Since the deflection seen in the spring, X, is reduced in this region, the force transmitted by the spring (F = kx) to the base is reduced. Therefore the mass–spring–damper system is isolating the harmonic force from the mounting base – referred to as vibration isolationVibration isolationVibration isolation is the process of isolating an object, such as a piece of equipment, from the source of vibrations.-Passive isolation:Passive vibration isolation systems consist essentially of a mass, spring and damper ....
In this region the force generated by the mass (F = ma) is dominating because the acceleration seen by the mass increases with the frequency. Since the deflection seen in the spring, X, is reduced in this region, the force transmitted by the spring (F = kx) to the base is reduced. Therefore the mass–spring–damper system is isolating the harmonic force from the mounting base – referred to as vibration isolationVibration isolationVibration isolation is the process of isolating an object, such as a piece of equipment, from the source of vibrations.-Passive isolation:Passive vibration isolation systems consist essentially of a mass, spring and damper ....
. Interestingly, more damping actually reduces the effects of vibration isolation when r ≫ 1 because the damping force (F = cv) is also transmitted to the base.
What causes resonance?
Resonance is simple to understand if you view the spring and mass as energy storage elements – with the mass storing kinetic energy and the spring storing potential energy. As discussed earlier, when the mass and spring have no external force acting on them they transfer energy back and forth at a rate equal to the natural frequency. In other words, if energy is to be efficiently pumped into both the mass and spring the energy source needs to feed the energy in at a rate equal to the natural frequency. Applying a force to the mass and spring is similar to pushing a child on swing, you need to push at the correct moment if you want the swing to get higher and higher. As in the case of the swing, the force applied does not necessarily have to be high to get large motions; the pushes just need to keep adding energy into the system.The damper, instead of storing energy, dissipates energy. Since the damping force is proportional to the velocity, the more the motion, the more the damper dissipates the energy. Therefore a point will come when the energy dissipated by the damper will equal the energy being fed in by the force. At this point, the system has reached its maximum amplitude and will continue to vibrate at this level as long as the force applied stays the same. If no damping exists, there is nothing to dissipate the energy and therefore theoretically the motion will continue to grow on into infinity.
Applying "complex" forces to the mass–spring–damper model
In a previous section only a simple harmonic force was applied to the model, but this can be extended considerably using two powerful mathematical tools. The first is the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
that takes a signal as a function of time (time domain
Time domain
Time domain is a term used to describe the analysis of mathematical functions, physical signals or time series of economic or environmental data, with respect to time. In the time domain, the signal or function's value is known for all real numbers, for the case of continuous time, or at various...
) and breaks it down into its harmonic components as a function of frequency (frequency domain
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
). For example, let us apply a force to the mass–spring–damper model that repeats the following cycle – a force equal to 1 newton for 0.5 second and then no force for 0.5 second. This type of force has the shape of a 1 Hz square wave
Square wave
A square wave is a kind of non-sinusoidal waveform, most typically encountered in electronics and signal processing. An ideal square wave alternates regularly and instantaneously between two levels...
.

Frequency spectrum
The frequency spectrum of a time-domain signal is a representation of that signal in the frequency domain. The frequency spectrum can be generated via a Fourier transform of the signal, and the resulting values are usually presented as amplitude and phase, both plotted versus frequency.Any signal...
that presents the magnitude of the harmonics that make up the square wave (the phase is also generated, but is typically of less concern and therefore is often not plotted). The Fourier transform can also be used to analyze non-periodic
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
functions such as transients (e.g. impulses) and random functions. With the advent of the modern computer the Fourier transform is almost always computed using the Fast Fourier Transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT) computer algorithm in combination with a window function
Window function
In signal processing, a window function is a mathematical function that is zero-valued outside of some chosen interval. For instance, a function that is constant inside the interval and zero elsewhere is called a rectangular window, which describes the shape of its graphical representation...
.
In the case of our square wave force, the first component is actually a constant force of 0.5 newton and is represented by a value at "0" Hz in the frequency spectrum. The next component is a 1 Hz sine wave with an amplitude of 0.64. This is shown by the line at 1 Hz. The remaining components are at odd frequencies and it takes an infinite amount of sine waves to generate the perfect square wave. Hence, the Fourier transform allows you to interpret the force as a sum of sinusoidal forces being applied instead of a more "complex" force (e.g. a square wave).
In the previous section, the vibration solution was given for a single harmonic force, but the Fourier transform will in general give multiple harmonic forces. The second mathematical tool, "the principle of superposition"
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
, allows you to sum the solutions from multiple forces if the system is linear
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
. In the case of the spring–mass–damper model, the system is linear if the spring force is proportional to the displacement and the damping is proportional to the velocity over the range of motion of interest. Hence, the solution to the problem with a square wave is summing the predicted vibration from each one of the harmonic forces found in the frequency spectrum of the square wave.
Frequency response model
We can view the solution of a vibration problem as an input/output relation – where the force is the input and the output is the vibration. If we represent the force and vibration in the frequency domain (magnitude and phase) we can write the following relation:
 is called the frequency response
is called the frequency responseFrequency response
Frequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input...
function (also referred to as the transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
, but not technically as accurate) and has both a magnitude and phase component (if represented as a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, a real and imaginary component). The magnitude of the frequency response function (FRF) was presented earlier for the mass–spring–damper system.
 where
where 
The phase of the FRF was also presented earlier as:

For example, let us calculate the FRF for a mass–spring–damper system with a mass of 1 kg, spring stiffness of 1.93 N/mm and a damping ratio of 0.1. The values of the spring and mass give a natural frequency of 7 Hz for this specific system. If we apply the 1 Hz square wave from earlier we can calculate the predicted vibration of the mass. The figure illustrates the resulting vibration. It happens in this example that the fourth harmonic of the square wave falls at 7 Hz. The frequency response of the mass–spring–damper therefore outputs a high 7 Hz vibration even though the input force had a relatively low 7 Hz harmonic. This example highlights that the resulting vibration is dependent on both the forcing function and the system that the force is applied to.

The frequency response function (FRF) does not necessarily have to be calculated from the knowledge of the mass, damping, and stiffness of the system, but can be measured experimentally. For example, if you apply a known force and sweep the frequency and then measure the resulting vibration you can calculate the frequency response function and then characterize the system. This technique is used in the field of experimental modal analysis
Modal analysis
Modal analysis is the study of the dynamic properties of structures under vibrational excitation.Modal analysis is the field of measuring and analysing the dynamic response of structures and or fluids when excited by an input...
to determine the vibration characteristics of a structure.
Multiple degrees of freedom systems and mode shapes
The simple mass–spring damper model is the foundation of vibration analysis, but what about more complex systems? The mass–spring–damper model described above is called a single degree of freedomDegrees of freedom (engineering)
In mechanics, degrees of freedom are the set of independent displacements and/or rotations that specify completely the displaced or deformed position and orientation of the body or system...
(SDOF) model since we have assumed the mass only moves up and down. In the case of more complex systems we need to discretize the system into more masses and allow them to move in more than one direction – adding degrees of freedom. The major concepts of multiple degrees of freedom (MDOF) can be understood by looking at just a 2 degree of freedom model as shown in the figure.



We can rewrite this in matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
format:

A more compact form of this matrix equation can be written as:

where

 and
and  are symmetric matrices referred respectively as the mass, damping, and stiffness matrices. The matrices are NxN square matrices where N is the number of degrees of freedom of the system.
are symmetric matrices referred respectively as the mass, damping, and stiffness matrices. The matrices are NxN square matrices where N is the number of degrees of freedom of the system.In the following analysis we will consider the case where there is no damping and no applied forces (i.e. free vibration). The solution of a viscously damped system is somewhat more complicated.

This differential equation can be solved by assuming the following type of solution:

Note: Using the exponential solution of
 is a mathematical trick used to solve linear differential equations. If we use Euler's formula
is a mathematical trick used to solve linear differential equations. If we use Euler's formulaEuler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
and take only the real part of the solution it is the same cosine solution for the 1 DOF system. The exponential solution is only used because it easier to manipulate mathematically.
The equation then becomes:

Since
 cannot equal zero the equation reduces to the following.
cannot equal zero the equation reduces to the following.
Eigenvalue problem
This is referred to an eigenvalue problem in mathematics and can be put in the standard format by pre-multiplying the equation by

and if we let
 and
and 

The solution to the problem results in N eigenvalues (i.e.
 ), where N corresponds to the number of degrees of freedom. The eigenvalues provide the natural frequencies of the system. When these eigenvalues are substituted back into the original set of equations, the values of
), where N corresponds to the number of degrees of freedom. The eigenvalues provide the natural frequencies of the system. When these eigenvalues are substituted back into the original set of equations, the values of  that correspond to each eigenvalue are called the eigenvectors. These eigenvectors represent the mode shapes of the system. The solution of an eigenvalue problem can be quite cumbersome (especially for problems with many degrees of freedom), but fortunately most math analysis programs have eigenvalue routines.
that correspond to each eigenvalue are called the eigenvectors. These eigenvectors represent the mode shapes of the system. The solution of an eigenvalue problem can be quite cumbersome (especially for problems with many degrees of freedom), but fortunately most math analysis programs have eigenvalue routines.The eigenvalues and eigenvectors are often written in the following matrix format and describe the modal model of the system:
 and
and 
A simple example using our 2 DOF model can help illustrate the concepts. Let both masses have a mass of 1 kg and the stiffness of all three springs equal 1000 N/m. The mass and stiffness matrix for this problem are then:
 and
and 
Then

The eigenvalues for this problem given by an eigenvalue routine will be:

The natural frequencies in the units of hertz are then (remembering
 )
)  and
and  .
.The two mode shapes for the respective natural frequencies are given as:

Since the system is a 2 DOF system, there are two modes with their respective natural frequencies and shapes. The mode shape vectors are not the absolute motion, but just describe relative motion of the degrees of freedom. In our case the first mode shape vector is saying that the masses are moving together in phase since they have the same value and sign. In the case of the second mode shape vector, each mass is moving in opposite direction at the same rate.
Illustration of a multiple DOF problem
When there are many degrees of freedom, the best method of visualizing the mode shapes is by animating them. An example of animated mode shapes is shown in the figure below for a cantileverCantilever
A cantilever is a beam anchored at only one end. The beam carries the load to the support where it is resisted by moment and shear stress. Cantilever construction allows for overhanging structures without external bracing. Cantilevers can also be constructed with trusses or slabs.This is in...
ed I-beam
I-beam
-beams, also known as H-beams, W-beams , rolled steel joist , or double-T are beams with an - or H-shaped cross-section. The horizontal elements of the "" are flanges, while the vertical element is the web...
. In this case, a finite element
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
model was used to generate the mass and stiffness matrices and solve the eigenvalue problem. Even this relatively simple model has over 100 degrees of freedom and hence as many natural frequencies and mode shapes. In general only the first few modes are important.
The mode shapes of a cantilevered I-beam
Multiple DOF problem converted to a single DOF problem
The eigenvectors have very important properties called orthogonality properties. These properties can be used to greatly simplify the solution of multi-degree of freedom models. It can be shown that the eigenvectors have the following properties:

 and
and  are diagonal matrices
are diagonal matricesDiagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
that contain the modal mass and stiffness values for each one of the modes. (Note: Since the eigenvectors (mode shapes) can be arbitrarily scaled, the orthogonality properties are often used to scale the eigenvectors so the modal mass value for each mode is equal to 1. The modal mass matrix is therefore an identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
)
These properties can be used to greatly simplify the solution of multi-degree of freedom models by making the following coordinate transformation.

If we use this coordinate transformation in our original free vibration differential equation we get the following equation.

We can take advantage of the orthogonality properties by premultiplying this equation by


The orthogonality properties then simplify this equation to:

This equation is the foundation of vibration analysis for multiple degree of freedom systems. A similar type of result can be derived for damped systems. The key is that the modal and stiffness matrices are diagonal matrices and therefore we have "decoupled" the equations. In other words, we have transformed our problem from a large unwieldy multiple degree of freedom problem into many single degree of freedom problems that can be solved using the same methods outlined above.
Instead of solving for x we are instead solving for q, referred to as the modal coordinates or modal participation factors.
It may be clearer to understand if we write
 as:
as:
Written in this form we can see that the vibration at each of the degrees of freedom is just a linear sum of the mode shapes. Furthermore, how much each mode "participates" in the final vibration is defined by q, its modal participation factor.
See also
Vibration refers to mechanical oscillations about an equilibrium point. The oscillations may be periodicPeriodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
such as the motion of a pendulum or random such as the movement of a tire on a gravel road.
Vibration is occasionally "desirable". For example the motion of a tuning fork
Tuning fork
A tuning fork is an acoustic resonator in the form of a two-pronged fork with the prongs formed from a U-shaped bar of elastic metal . It resonates at a specific constant pitch when set vibrating by striking it against a surface or with an object, and emits a pure musical tone after waiting a...
, the reed in a woodwind instrument
Woodwind instrument
A woodwind instrument is a musical instrument which produces sound when the player blows air against a sharp edge or through a reed, causing the air within its resonator to vibrate...
or harmonica
Harmonica
The harmonica, also called harp, French harp, blues harp, and mouth organ, is a free reed wind instrument used primarily in blues and American folk music, jazz, country, and rock and roll. It is played by blowing air into it or drawing air out by placing lips over individual holes or multiple holes...
, or the cone of a loudspeaker
Loudspeaker
A loudspeaker is an electroacoustic transducer that produces sound in response to an electrical audio signal input. Non-electrical loudspeakers were developed as accessories to telephone systems, but electronic amplification by vacuum tube made loudspeakers more generally useful...
is desirable vibration, necessary for the correct functioning of the various devices.
More often, vibration is undesirable, wasting energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
and creating unwanted sound
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
– noise
Noise
In common use, the word noise means any unwanted sound. In both analog and digital electronics, noise is random unwanted perturbation to a wanted signal; it is called noise as a generalisation of the acoustic noise heard when listening to a weak radio transmission with significant electrical noise...
. For example, the vibrational motions of engine
Engine
An engine or motor is a machine designed to convert energy into useful mechanical motion. Heat engines, including internal combustion engines and external combustion engines burn a fuel to create heat which is then used to create motion...
s, electric motor
Electric motor
An electric motor converts electrical energy into mechanical energy.Most electric motors operate through the interaction of magnetic fields and current-carrying conductors to generate force...
s, or any mechanical device
Machine
A machine manages power to accomplish a task, examples include, a mechanical system, a computing system, an electronic system, and a molecular machine. In common usage, the meaning is that of a device having parts that perform or assist in performing any type of work...
in operation are typically unwanted. Such vibrations can be caused by imbalances
Engine balance
Engine balance is the design, construction and tuning of an engine to run smoothly. Improving engine balance reduces vibration and other stresses and can improve the overall performance, efficiency, cost of ownership and reliability of the engine, as well as reducing the stress on other machinery...
in the rotating parts, uneven friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
, the meshing of gear
Gear
A gear is a rotating machine part having cut teeth, or cogs, which mesh with another toothed part in order to transmit torque. Two or more gears working in tandem are called a transmission and can produce a mechanical advantage through a gear ratio and thus may be considered a simple machine....
teeth, etc. Careful designs usually minimize unwanted vibrations.
The study of sound and vibration are closely related. Sound, or "pressure wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
s", are generated by vibrating structures (e.g. vocal cords); these pressure waves can also induce the vibration of structures (e.g. ear drum). Hence, when trying to reduce noise it is often a problem in trying to reduce vibration.


Types of vibration
Free vibration occurs when a mechanical system is set off with an initial input and then allowed to vibrate freely. Examples of this type of vibration are pulling a child back on a swing and then letting go or hitting a tuning fork and letting it ring. The mechanical system will then vibrate at one or more of its "natural frequencyResonance
In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...
" and damp down to zero.
Forced vibration is when an alternating force or motion is applied to a mechanical system. Examples of this type of vibration include a shaking washing machine due to an imbalance, transportation vibration (caused by truck engine, springs, road, etc.), or the vibration of a building during an earthquake
Earthquake
An earthquake is the result of a sudden release of energy in the Earth's crust that creates seismic waves. The seismicity, seismism or seismic activity of an area refers to the frequency, type and size of earthquakes experienced over a period of time...
. In forced vibration the frequency of the vibration is the frequency of the force or motion applied, with order of magnitude being dependent on the actual mechanical system.
Vibration testing
Vibration testing is accomplished by introducing a forcing function into a structure, usually with some type of shaker. Alternately, a DUT (device under test) is attached to the "table" of a shaker. For relatively low frequency forcing, servohydraulic (electrohydraulic) shakers are used. For higher frequencies, electrodynamic shakers are used. Generally, one or more "input" or "control" points located on the DUT-side of a fixture is kept at a specified acceleration. Other "response" points experience maximum vibration level (resonance) or minimum vibration level (anti-resonance).Two typical types of vibration tests performed are random- and sine test. Sine (one-frequency-at-a-time) tests are performed to survey the structural response of the device under test (DUT). A random (all frequencies at once) test is generally considered to more closely replicate a real world environment, such as road inputs to a moving automobile.
Most vibration testing is conducted in a single DUT axis at a time, even though most real-world vibration occurs in various axes simultaneously. MIL-STD-810G, released in late 2008, Test Method 527, calls for multiple exciter testing.
Vibration analysis
The fundamentals of vibration analysis can be understood by studying the simple massMass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
–spring
Spring (device)
A spring is an elastic object used to store mechanical energy. Springs are usually made out of spring steel. Small springs can be wound from pre-hardened stock, while larger ones are made from annealed steel and hardened after fabrication...
–damper
Shock absorber
A shock absorber is a mechanical device designed to smooth out or damp shock impulse, and dissipate kinetic energy. It is a type of dashpot.-Nomenclature:...
model. Indeed, even a complex structure such as an automobile body can be modeled as a "summation" of simple mass–spring–damper models. The mass–spring–damper model is an example of a simple harmonic oscillator. The mathematics used to describe its behavior is identical to other simple harmonic oscillators such as the RLC circuit
RLC circuit
An RLC circuit is an electrical circuit consisting of a resistor, an inductor, and a capacitor, connected in series or in parallel. The RLC part of the name is due to those letters being the usual electrical symbols for resistance, inductance and capacitance respectively...
.
Note: In this article the step by step mathematical derivations will not be included, but will focus on the major equations and concepts in vibration analysis. Please refer to the references at the end of the article for detailed derivations.
Free vibration without damping

The force applied to the mass by the spring is proportional to the amount the spring is stretched "x" (we will assume the spring is already compressed due to the weight of the mass). The proportionality constant, k, is the stiffness of the spring and has units of force/distance (e.g. lbf/in or N/m). The negative sign indicates that the force is always opposing the motion of the mass attached to it.

The force generated by the mass is proportional to the acceleration of the mass as given by Newton’s second law of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
.

The sum of the forces on the mass then generates this ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
:



This solution says that it will oscillate with simple harmonic motion
Simple harmonic motion
Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
that has an amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of A and a frequency of
 The number
The number  is one of the most important quantities in vibration analysis and is called the undamped natural frequency. For the simple mass–spring system,
is one of the most important quantities in vibration analysis and is called the undamped natural frequency. For the simple mass–spring system,  is defined as:
is defined as:
Note: Angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
 (
( ) with the units of radians per second is often used in equations because it simplifies the equations, but is normally converted to “standard” frequency (units of Hz
) with the units of radians per second is often used in equations because it simplifies the equations, but is normally converted to “standard” frequency (units of HzHertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
or equivalently cycles per second) when stating the frequency of a system.
If you know the mass and stiffness of the system you can determine the frequency at which the system will vibrate once it is set in motion by an initial disturbance using the above stated formula. Every vibrating system has one or more natural frequencies that it will vibrate at once it is disturbed. This simple relation can be used to understand in general what will happen to a more complex system once we add mass or stiffness. For example, the above formula explains why when a car or truck is fully loaded the suspension will feel “softer” than unloaded because the mass has increased and therefore reduced the natural frequency of the system.
What causes the system to vibrate: from conservation of energy point of view
Vibrational motion could be understood in terms of conservation of energyConservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
. In the above example we have extended the spring by a value of
 and therefore have stored some potential energy
and therefore have stored some potential energyPotential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
(
 ) in the spring. Once we let go of the spring, the spring tries to return to its un-stretched state (which is the minimum potential energy state) and in the process accelerates the mass. At the point where the spring has reached its un-stretched state all the potential energy that we supplied by stretching it has been transformed into kinetic energy
) in the spring. Once we let go of the spring, the spring tries to return to its un-stretched state (which is the minimum potential energy state) and in the process accelerates the mass. At the point where the spring has reached its un-stretched state all the potential energy that we supplied by stretching it has been transformed into kinetic energyKinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
(
 ). The mass then begins to decelerate because it is now compressing the spring and in the process transferring the kinetic energy back to its potential. Thus oscillation of the spring amounts to the transferring back and forth of the kinetic energy into potential energy.
). The mass then begins to decelerate because it is now compressing the spring and in the process transferring the kinetic energy back to its potential. Thus oscillation of the spring amounts to the transferring back and forth of the kinetic energy into potential energy.In our simple model the mass will continue to oscillate forever at the same magnitude, but in a real system there is always something called damping that dissipates the energy, eventually bringing it to rest.
Free vibration with damping


By summing the forces on the mass we get the following ordinary differential equation:

The solution to this equation depends on the amount of damping. If the damping is small enough the system will still vibrate, but eventually, over time, will stop vibrating. This case is called underdamping – this case is of most interest in vibration analysis. If we increase the damping just to the point where the system no longer oscillates we reach the point of critical damping (if the damping is increased past critical damping the system is called overdamped). The value that the damping coefficient needs to reach for critical damping in the mass spring damper model is:

To characterize the amount of damping in a system a ratio called the damping ratio
Damping ratio
[[Image:Damped spring.gif|right|frame|Underdamped [[spring–mass system]] with ζ 1 , and is referred to as overdamped.*Underdamped:If s is a complex number, then the solution is a decaying exponential combined with an oscillatory portion that looks like \exp...
(also known as damping factor and % critical damping) is used. This damping ratio is just a ratio of the actual damping over the amount of damping required to reach critical damping. The formula for the damping ratio (
 ) of the mass spring damper model is:
) of the mass spring damper model is:
For example, metal structures (e.g. airplane fuselage, engine crankshaft) will have damping factors less than 0.05 while automotive suspensions in the range of 0.2–0.3.
The solution to the underdamped system for the mass spring damper model is the following:


 the phase shift, are determined by the amount the spring is stretched. The formulas for these values can be found in the references.
the phase shift, are determined by the amount the spring is stretched. The formulas for these values can be found in the references.Damped and undamped natural frequencies
The major points to note from the solution are the exponential term and the cosine function. The exponential term defines how quickly the system “damps” down – the larger the damping ratio, the quicker it damps to zero. The cosine function is the oscillating portion of the solution, but the frequency of the oscillations is different from the undamped case.The frequency in this case is called the "damped natural frequency",
 and is related to the undamped natural frequency by the following formula:
and is related to the undamped natural frequency by the following formula:
The damped natural frequency is less than the undamped natural frequency, but for many practical cases the damping ratio is relatively small and hence the difference is negligible. Therefore the damped and undamped description are often dropped when stating the natural frequency (e.g. with 0.1 damping ratio, the damped natural frequency is only 1% less than the undamped).
The plots to the side present how 0.1 and 0.3 damping ratios effect how the system will “ring” down over time. What is often done in practice is to experimentally measure the free vibration after an impact (for example by a hammer) and then determine the natural frequency of the system by measuring the rate of oscillation as well as the damping ratio by measuring the rate of decay. The natural frequency and damping ratio are not only important in free vibration, but also characterize how a system will behave under forced vibration.
Forced vibration with damping
In this section we will see the behavior of the spring mass damper model when we add a harmonic force in the form below. A force of this type could, for example, be generated by a rotating imbalance.
If we again sum the forces on the mass we get the following ordinary differential equation:

The steady state
Steady state
A system in a steady state has numerous properties that are unchanging in time. This implies that for any property p of the system, the partial derivative with respect to time is zero:...
solution of this problem can be written as:

The result states that the mass will oscillate at the same frequency, f, of the applied force, but with a phase shift

The amplitude of the vibration “X” is defined by the following formula.

Where “r” is defined as the ratio of the harmonic force frequency over the undamped natural frequency of the mass–spring–damper model.

The phase shift ,
 is defined by the following formula.
is defined by the following formula.

 ) the amplitude of the vibration can get extremely high. This phenomenon is called resonance
) the amplitude of the vibration can get extremely high. This phenomenon is called resonanceMechanical resonance
Mechanical resonance is the tendency of a mechanical system to absorb more energy when the frequency of its oscillations matches the system's natural frequency of vibration than it does at other frequencies...
(subsequently the natural frequency of a system is often referred to as the resonant frequency). In rotor bearing systems any rotational speed that excites a resonant frequency is referred to as a critical speed
Critical speed
In solid mechanics, in the field of rotordynamics, the critical speed is the theoretical angular velocity which excites the natural frequency of a rotating object, such as a shaft, propeller, leadscrew, or gear. As the speed of rotation approaches the object's natural frequency, the object begins...
.
If resonance occurs in a mechanical system it can be very harmful – leading to eventual failure of the system. Consequently, one of the major reasons for vibration analysis is to predict when this type of resonance may occur and then to determine what steps to take to prevent it from occurring. As the amplitude plot shows, adding damping can significantly reduce the magnitude of the vibration. Also, the magnitude can be reduced if the natural frequency can be shifted away from the forcing frequency by changing the stiffness or mass of the system. If the system cannot be changed, perhaps the forcing frequency can be shifted (for example, changing the speed of the machine generating the force).
The following are some other points in regards to the forced vibration shown in the frequency response plots.
- At a given frequency ratio, the amplitude of the vibration, X, is directly proportional to the amplitude of the force
 (e.g. if you double the force, the vibration doubles)
(e.g. if you double the force, the vibration doubles) - With little or no damping, the vibration is in phase with the forcing frequency when the frequency ratio r < 1 and 180 degrees out of phase when the frequency ratio r > 1
- When r ≪ 1 the amplitude is just the deflection of the spring under the static force
 This deflection is called the static deflection
This deflection is called the static deflection  Hence, when r ≪ 1 the effects of the damper and the mass are minimal.
Hence, when r ≪ 1 the effects of the damper and the mass are minimal. - When r ≫ 1 the amplitude of the vibration is actually less than the static deflection
 In this region the force generated by the mass (F = ma) is dominating because the acceleration seen by the mass increases with the frequency. Since the deflection seen in the spring, X, is reduced in this region, the force transmitted by the spring (F = kx) to the base is reduced. Therefore the mass–spring–damper system is isolating the harmonic force from the mounting base – referred to as vibration isolationVibration isolationVibration isolation is the process of isolating an object, such as a piece of equipment, from the source of vibrations.-Passive isolation:Passive vibration isolation systems consist essentially of a mass, spring and damper ....
In this region the force generated by the mass (F = ma) is dominating because the acceleration seen by the mass increases with the frequency. Since the deflection seen in the spring, X, is reduced in this region, the force transmitted by the spring (F = kx) to the base is reduced. Therefore the mass–spring–damper system is isolating the harmonic force from the mounting base – referred to as vibration isolationVibration isolationVibration isolation is the process of isolating an object, such as a piece of equipment, from the source of vibrations.-Passive isolation:Passive vibration isolation systems consist essentially of a mass, spring and damper ....
. Interestingly, more damping actually reduces the effects of vibration isolation when r ≫ 1 because the damping force (F = cv) is also transmitted to the base.
What causes resonance?
Resonance is simple to understand if you view the spring and mass as energy storage elements – with the mass storing kinetic energy and the spring storing potential energy. As discussed earlier, when the mass and spring have no external force acting on them they transfer energy back and forth at a rate equal to the natural frequency. In other words, if energy is to be efficiently pumped into both the mass and spring the energy source needs to feed the energy in at a rate equal to the natural frequency. Applying a force to the mass and spring is similar to pushing a child on swing, you need to push at the correct moment if you want the swing to get higher and higher. As in the case of the swing, the force applied does not necessarily have to be high to get large motions; the pushes just need to keep adding energy into the system.The damper, instead of storing energy, dissipates energy. Since the damping force is proportional to the velocity, the more the motion, the more the damper dissipates the energy. Therefore a point will come when the energy dissipated by the damper will equal the energy being fed in by the force. At this point, the system has reached its maximum amplitude and will continue to vibrate at this level as long as the force applied stays the same. If no damping exists, there is nothing to dissipate the energy and therefore theoretically the motion will continue to grow on into infinity.
Applying "complex" forces to the mass–spring–damper model
In a previous section only a simple harmonic force was applied to the model, but this can be extended considerably using two powerful mathematical tools. The first is the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
that takes a signal as a function of time (time domain
Time domain
Time domain is a term used to describe the analysis of mathematical functions, physical signals or time series of economic or environmental data, with respect to time. In the time domain, the signal or function's value is known for all real numbers, for the case of continuous time, or at various...
) and breaks it down into its harmonic components as a function of frequency (frequency domain
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
). For example, let us apply a force to the mass–spring–damper model that repeats the following cycle – a force equal to 1 newton for 0.5 second and then no force for 0.5 second. This type of force has the shape of a 1 Hz square wave
Square wave
A square wave is a kind of non-sinusoidal waveform, most typically encountered in electronics and signal processing. An ideal square wave alternates regularly and instantaneously between two levels...
.

Frequency spectrum
The frequency spectrum of a time-domain signal is a representation of that signal in the frequency domain. The frequency spectrum can be generated via a Fourier transform of the signal, and the resulting values are usually presented as amplitude and phase, both plotted versus frequency.Any signal...
that presents the magnitude of the harmonics that make up the square wave (the phase is also generated, but is typically of less concern and therefore is often not plotted). The Fourier transform can also be used to analyze non-periodic
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
functions such as transients (e.g. impulses) and random functions. With the advent of the modern computer the Fourier transform is almost always computed using the Fast Fourier Transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT) computer algorithm in combination with a window function
Window function
In signal processing, a window function is a mathematical function that is zero-valued outside of some chosen interval. For instance, a function that is constant inside the interval and zero elsewhere is called a rectangular window, which describes the shape of its graphical representation...
.
In the case of our square wave force, the first component is actually a constant force of 0.5 newton and is represented by a value at "0" Hz in the frequency spectrum. The next component is a 1 Hz sine wave with an amplitude of 0.64. This is shown by the line at 1 Hz. The remaining components are at odd frequencies and it takes an infinite amount of sine waves to generate the perfect square wave. Hence, the Fourier transform allows you to interpret the force as a sum of sinusoidal forces being applied instead of a more "complex" force (e.g. a square wave).
In the previous section, the vibration solution was given for a single harmonic force, but the Fourier transform will in general give multiple harmonic forces. The second mathematical tool, "the principle of superposition"
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
, allows you to sum the solutions from multiple forces if the system is linear
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
. In the case of the spring–mass–damper model, the system is linear if the spring force is proportional to the displacement and the damping is proportional to the velocity over the range of motion of interest. Hence, the solution to the problem with a square wave is summing the predicted vibration from each one of the harmonic forces found in the frequency spectrum of the square wave.
Frequency response model
We can view the solution of a vibration problem as an input/output relation – where the force is the input and the output is the vibration. If we represent the force and vibration in the frequency domain (magnitude and phase) we can write the following relation:
 is called the frequency response
is called the frequency responseFrequency response
Frequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input...
function (also referred to as the transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
, but not technically as accurate) and has both a magnitude and phase component (if represented as a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, a real and imaginary component). The magnitude of the frequency response function (FRF) was presented earlier for the mass–spring–damper system.
 where
where 
The phase of the FRF was also presented earlier as:

For example, let us calculate the FRF for a mass–spring–damper system with a mass of 1 kg, spring stiffness of 1.93 N/mm and a damping ratio of 0.1. The values of the spring and mass give a natural frequency of 7 Hz for this specific system. If we apply the 1 Hz square wave from earlier we can calculate the predicted vibration of the mass. The figure illustrates the resulting vibration. It happens in this example that the fourth harmonic of the square wave falls at 7 Hz. The frequency response of the mass–spring–damper therefore outputs a high 7 Hz vibration even though the input force had a relatively low 7 Hz harmonic. This example highlights that the resulting vibration is dependent on both the forcing function and the system that the force is applied to.

The frequency response function (FRF) does not necessarily have to be calculated from the knowledge of the mass, damping, and stiffness of the system, but can be measured experimentally. For example, if you apply a known force and sweep the frequency and then measure the resulting vibration you can calculate the frequency response function and then characterize the system. This technique is used in the field of experimental modal analysis
Modal analysis
Modal analysis is the study of the dynamic properties of structures under vibrational excitation.Modal analysis is the field of measuring and analysing the dynamic response of structures and or fluids when excited by an input...
to determine the vibration characteristics of a structure.
Multiple degrees of freedom systems and mode shapes
The simple mass–spring damper model is the foundation of vibration analysis, but what about more complex systems? The mass–spring–damper model described above is called a single degree of freedomDegrees of freedom (engineering)
In mechanics, degrees of freedom are the set of independent displacements and/or rotations that specify completely the displaced or deformed position and orientation of the body or system...
(SDOF) model since we have assumed the mass only moves up and down. In the case of more complex systems we need to discretize the system into more masses and allow them to move in more than one direction – adding degrees of freedom. The major concepts of multiple degrees of freedom (MDOF) can be understood by looking at just a 2 degree of freedom model as shown in the figure.



We can rewrite this in matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
format:

A more compact form of this matrix equation can be written as:

where

 and
and  are symmetric matrices referred respectively as the mass, damping, and stiffness matrices. The matrices are NxN square matrices where N is the number of degrees of freedom of the system.
are symmetric matrices referred respectively as the mass, damping, and stiffness matrices. The matrices are NxN square matrices where N is the number of degrees of freedom of the system.In the following analysis we will consider the case where there is no damping and no applied forces (i.e. free vibration). The solution of a viscously damped system is somewhat more complicated.

This differential equation can be solved by assuming the following type of solution:

Note: Using the exponential solution of
 is a mathematical trick used to solve linear differential equations. If we use Euler's formula
is a mathematical trick used to solve linear differential equations. If we use Euler's formulaEuler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
and take only the real part of the solution it is the same cosine solution for the 1 DOF system. The exponential solution is only used because it easier to manipulate mathematically.
The equation then becomes:

Since
 cannot equal zero the equation reduces to the following.
cannot equal zero the equation reduces to the following.
Eigenvalue problem
This is referred to an eigenvalue problem in mathematics and can be put in the standard format by pre-multiplying the equation by

and if we let
 and
and 

The solution to the problem results in N eigenvalues (i.e.
 ), where N corresponds to the number of degrees of freedom. The eigenvalues provide the natural frequencies of the system. When these eigenvalues are substituted back into the original set of equations, the values of
), where N corresponds to the number of degrees of freedom. The eigenvalues provide the natural frequencies of the system. When these eigenvalues are substituted back into the original set of equations, the values of  that correspond to each eigenvalue are called the eigenvectors. These eigenvectors represent the mode shapes of the system. The solution of an eigenvalue problem can be quite cumbersome (especially for problems with many degrees of freedom), but fortunately most math analysis programs have eigenvalue routines.
that correspond to each eigenvalue are called the eigenvectors. These eigenvectors represent the mode shapes of the system. The solution of an eigenvalue problem can be quite cumbersome (especially for problems with many degrees of freedom), but fortunately most math analysis programs have eigenvalue routines.The eigenvalues and eigenvectors are often written in the following matrix format and describe the modal model of the system:
 and
and 
A simple example using our 2 DOF model can help illustrate the concepts. Let both masses have a mass of 1 kg and the stiffness of all three springs equal 1000 N/m. The mass and stiffness matrix for this problem are then:
 and
and 
Then

The eigenvalues for this problem given by an eigenvalue routine will be:

The natural frequencies in the units of hertz are then (remembering
 )
)  and
and  .
.The two mode shapes for the respective natural frequencies are given as:

Since the system is a 2 DOF system, there are two modes with their respective natural frequencies and shapes. The mode shape vectors are not the absolute motion, but just describe relative motion of the degrees of freedom. In our case the first mode shape vector is saying that the masses are moving together in phase since they have the same value and sign. In the case of the second mode shape vector, each mass is moving in opposite direction at the same rate.
Illustration of a multiple DOF problem
When there are many degrees of freedom, the best method of visualizing the mode shapes is by animating them. An example of animated mode shapes is shown in the figure below for a cantileverCantilever
A cantilever is a beam anchored at only one end. The beam carries the load to the support where it is resisted by moment and shear stress. Cantilever construction allows for overhanging structures without external bracing. Cantilevers can also be constructed with trusses or slabs.This is in...
ed I-beam
I-beam
-beams, also known as H-beams, W-beams , rolled steel joist , or double-T are beams with an - or H-shaped cross-section. The horizontal elements of the "" are flanges, while the vertical element is the web...
. In this case, a finite element
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
model was used to generate the mass and stiffness matrices and solve the eigenvalue problem. Even this relatively simple model has over 100 degrees of freedom and hence as many natural frequencies and mode shapes. In general only the first few modes are important.
The mode shapes of a cantilevered I-beam
Multiple DOF problem converted to a single DOF problem
The eigenvectors have very important properties called orthogonality properties. These properties can be used to greatly simplify the solution of multi-degree of freedom models. It can be shown that the eigenvectors have the following properties:

 and
and  are diagonal matrices
are diagonal matricesDiagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
that contain the modal mass and stiffness values for each one of the modes. (Note: Since the eigenvectors (mode shapes) can be arbitrarily scaled, the orthogonality properties are often used to scale the eigenvectors so the modal mass value for each mode is equal to 1. The modal mass matrix is therefore an identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
)
These properties can be used to greatly simplify the solution of multi-degree of freedom models by making the following coordinate transformation.

If we use this coordinate transformation in our original free vibration differential equation we get the following equation.

We can take advantage of the orthogonality properties by premultiplying this equation by


The orthogonality properties then simplify this equation to:

This equation is the foundation of vibration analysis for multiple degree of freedom systems. A similar type of result can be derived for damped systems. The key is that the modal and stiffness matrices are diagonal matrices and therefore we have "decoupled" the equations. In other words, we have transformed our problem from a large unwieldy multiple degree of freedom problem into many single degree of freedom problems that can be solved using the same methods outlined above.
Instead of solving for x we are instead solving for q, referred to as the modal coordinates or modal participation factors.
It may be clearer to understand if we write
 as:
as:
Written in this form we can see that the vibration at each of the degrees of freedom is just a linear sum of the mode shapes. Furthermore, how much each mode "participates" in the final vibration is defined by q, its modal participation factor.
See also
Vibration refers to mechanical oscillations about an equilibrium point. The oscillations may be periodicPeriodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
such as the motion of a pendulum or random such as the movement of a tire on a gravel road.
Vibration is occasionally "desirable". For example the motion of a tuning fork
Tuning fork
A tuning fork is an acoustic resonator in the form of a two-pronged fork with the prongs formed from a U-shaped bar of elastic metal . It resonates at a specific constant pitch when set vibrating by striking it against a surface or with an object, and emits a pure musical tone after waiting a...
, the reed in a woodwind instrument
Woodwind instrument
A woodwind instrument is a musical instrument which produces sound when the player blows air against a sharp edge or through a reed, causing the air within its resonator to vibrate...
or harmonica
Harmonica
The harmonica, also called harp, French harp, blues harp, and mouth organ, is a free reed wind instrument used primarily in blues and American folk music, jazz, country, and rock and roll. It is played by blowing air into it or drawing air out by placing lips over individual holes or multiple holes...
, or the cone of a loudspeaker
Loudspeaker
A loudspeaker is an electroacoustic transducer that produces sound in response to an electrical audio signal input. Non-electrical loudspeakers were developed as accessories to telephone systems, but electronic amplification by vacuum tube made loudspeakers more generally useful...
is desirable vibration, necessary for the correct functioning of the various devices.
More often, vibration is undesirable, wasting energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
and creating unwanted sound
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
– noise
Noise
In common use, the word noise means any unwanted sound. In both analog and digital electronics, noise is random unwanted perturbation to a wanted signal; it is called noise as a generalisation of the acoustic noise heard when listening to a weak radio transmission with significant electrical noise...
. For example, the vibrational motions of engine
Engine
An engine or motor is a machine designed to convert energy into useful mechanical motion. Heat engines, including internal combustion engines and external combustion engines burn a fuel to create heat which is then used to create motion...
s, electric motor
Electric motor
An electric motor converts electrical energy into mechanical energy.Most electric motors operate through the interaction of magnetic fields and current-carrying conductors to generate force...
s, or any mechanical device
Machine
A machine manages power to accomplish a task, examples include, a mechanical system, a computing system, an electronic system, and a molecular machine. In common usage, the meaning is that of a device having parts that perform or assist in performing any type of work...
in operation are typically unwanted. Such vibrations can be caused by imbalances
Engine balance
Engine balance is the design, construction and tuning of an engine to run smoothly. Improving engine balance reduces vibration and other stresses and can improve the overall performance, efficiency, cost of ownership and reliability of the engine, as well as reducing the stress on other machinery...
in the rotating parts, uneven friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
, the meshing of gear
Gear
A gear is a rotating machine part having cut teeth, or cogs, which mesh with another toothed part in order to transmit torque. Two or more gears working in tandem are called a transmission and can produce a mechanical advantage through a gear ratio and thus may be considered a simple machine....
teeth, etc. Careful designs usually minimize unwanted vibrations.
The study of sound and vibration are closely related. Sound, or "pressure wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
s", are generated by vibrating structures (e.g. vocal cords); these pressure waves can also induce the vibration of structures (e.g. ear drum). Hence, when trying to reduce noise it is often a problem in trying to reduce vibration.


Types of vibration
Free vibration occurs when a mechanical system is set off with an initial input and then allowed to vibrate freely. Examples of this type of vibration are pulling a child back on a swing and then letting go or hitting a tuning fork and letting it ring. The mechanical system will then vibrate at one or more of its "natural frequencyResonance
In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...
" and damp down to zero.
Forced vibration is when an alternating force or motion is applied to a mechanical system. Examples of this type of vibration include a shaking washing machine due to an imbalance, transportation vibration (caused by truck engine, springs, road, etc.), or the vibration of a building during an earthquake
Earthquake
An earthquake is the result of a sudden release of energy in the Earth's crust that creates seismic waves. The seismicity, seismism or seismic activity of an area refers to the frequency, type and size of earthquakes experienced over a period of time...
. In forced vibration the frequency of the vibration is the frequency of the force or motion applied, with order of magnitude being dependent on the actual mechanical system.
Vibration testing
Vibration testing is accomplished by introducing a forcing function into a structure, usually with some type of shaker. Alternately, a DUT (device under test) is attached to the "table" of a shaker. For relatively low frequency forcing, servohydraulic (electrohydraulic) shakers are used. For higher frequencies, electrodynamic shakers are used. Generally, one or more "input" or "control" points located on the DUT-side of a fixture is kept at a specified acceleration. Other "response" points experience maximum vibration level (resonance) or minimum vibration level (anti-resonance).Two typical types of vibration tests performed are random- and sine test. Sine (one-frequency-at-a-time) tests are performed to survey the structural response of the device under test (DUT). A random (all frequencies at once) test is generally considered to more closely replicate a real world environment, such as road inputs to a moving automobile.
Most vibration testing is conducted in a single DUT axis at a time, even though most real-world vibration occurs in various axes simultaneously. MIL-STD-810G, released in late 2008, Test Method 527, calls for multiple exciter testing.
Vibration analysis
The fundamentals of vibration analysis can be understood by studying the simple massMass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
–spring
Spring (device)
A spring is an elastic object used to store mechanical energy. Springs are usually made out of spring steel. Small springs can be wound from pre-hardened stock, while larger ones are made from annealed steel and hardened after fabrication...
–damper
Shock absorber
A shock absorber is a mechanical device designed to smooth out or damp shock impulse, and dissipate kinetic energy. It is a type of dashpot.-Nomenclature:...
model. Indeed, even a complex structure such as an automobile body can be modeled as a "summation" of simple mass–spring–damper models. The mass–spring–damper model is an example of a simple harmonic oscillator. The mathematics used to describe its behavior is identical to other simple harmonic oscillators such as the RLC circuit
RLC circuit
An RLC circuit is an electrical circuit consisting of a resistor, an inductor, and a capacitor, connected in series or in parallel. The RLC part of the name is due to those letters being the usual electrical symbols for resistance, inductance and capacitance respectively...
.
Note: In this article the step by step mathematical derivations will not be included, but will focus on the major equations and concepts in vibration analysis. Please refer to the references at the end of the article for detailed derivations.
Free vibration without damping

The force applied to the mass by the spring is proportional to the amount the spring is stretched "x" (we will assume the spring is already compressed due to the weight of the mass). The proportionality constant, k, is the stiffness of the spring and has units of force/distance (e.g. lbf/in or N/m). The negative sign indicates that the force is always opposing the motion of the mass attached to it.

The force generated by the mass is proportional to the acceleration of the mass as given by Newton’s second law of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
.

The sum of the forces on the mass then generates this ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
:



This solution says that it will oscillate with simple harmonic motion
Simple harmonic motion
Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
that has an amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of A and a frequency of
 The number
The number  is one of the most important quantities in vibration analysis and is called the undamped natural frequency. For the simple mass–spring system,
is one of the most important quantities in vibration analysis and is called the undamped natural frequency. For the simple mass–spring system,  is defined as:
is defined as:
Note: Angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
 (
( ) with the units of radians per second is often used in equations because it simplifies the equations, but is normally converted to “standard” frequency (units of Hz
) with the units of radians per second is often used in equations because it simplifies the equations, but is normally converted to “standard” frequency (units of HzHertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
or equivalently cycles per second) when stating the frequency of a system.
If you know the mass and stiffness of the system you can determine the frequency at which the system will vibrate once it is set in motion by an initial disturbance using the above stated formula. Every vibrating system has one or more natural frequencies that it will vibrate at once it is disturbed. This simple relation can be used to understand in general what will happen to a more complex system once we add mass or stiffness. For example, the above formula explains why when a car or truck is fully loaded the suspension will feel “softer” than unloaded because the mass has increased and therefore reduced the natural frequency of the system.
What causes the system to vibrate: from conservation of energy point of view
Vibrational motion could be understood in terms of conservation of energyConservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
. In the above example we have extended the spring by a value of
 and therefore have stored some potential energy
and therefore have stored some potential energyPotential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
(
 ) in the spring. Once we let go of the spring, the spring tries to return to its un-stretched state (which is the minimum potential energy state) and in the process accelerates the mass. At the point where the spring has reached its un-stretched state all the potential energy that we supplied by stretching it has been transformed into kinetic energy
) in the spring. Once we let go of the spring, the spring tries to return to its un-stretched state (which is the minimum potential energy state) and in the process accelerates the mass. At the point where the spring has reached its un-stretched state all the potential energy that we supplied by stretching it has been transformed into kinetic energyKinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
(
 ). The mass then begins to decelerate because it is now compressing the spring and in the process transferring the kinetic energy back to its potential. Thus oscillation of the spring amounts to the transferring back and forth of the kinetic energy into potential energy.
). The mass then begins to decelerate because it is now compressing the spring and in the process transferring the kinetic energy back to its potential. Thus oscillation of the spring amounts to the transferring back and forth of the kinetic energy into potential energy.In our simple model the mass will continue to oscillate forever at the same magnitude, but in a real system there is always something called damping that dissipates the energy, eventually bringing it to rest.
Free vibration with damping


By summing the forces on the mass we get the following ordinary differential equation:

The solution to this equation depends on the amount of damping. If the damping is small enough the system will still vibrate, but eventually, over time, will stop vibrating. This case is called underdamping – this case is of most interest in vibration analysis. If we increase the damping just to the point where the system no longer oscillates we reach the point of critical damping (if the damping is increased past critical damping the system is called overdamped). The value that the damping coefficient needs to reach for critical damping in the mass spring damper model is:

To characterize the amount of damping in a system a ratio called the damping ratio
Damping ratio
[[Image:Damped spring.gif|right|frame|Underdamped [[spring–mass system]] with ζ 1 , and is referred to as overdamped.*Underdamped:If s is a complex number, then the solution is a decaying exponential combined with an oscillatory portion that looks like \exp...
(also known as damping factor and % critical damping) is used. This damping ratio is just a ratio of the actual damping over the amount of damping required to reach critical damping. The formula for the damping ratio (
 ) of the mass spring damper model is:
) of the mass spring damper model is:
For example, metal structures (e.g. airplane fuselage, engine crankshaft) will have damping factors less than 0.05 while automotive suspensions in the range of 0.2–0.3.
The solution to the underdamped system for the mass spring damper model is the following:


 the phase shift, are determined by the amount the spring is stretched. The formulas for these values can be found in the references.
the phase shift, are determined by the amount the spring is stretched. The formulas for these values can be found in the references.Damped and undamped natural frequencies
The major points to note from the solution are the exponential term and the cosine function. The exponential term defines how quickly the system “damps” down – the larger the damping ratio, the quicker it damps to zero. The cosine function is the oscillating portion of the solution, but the frequency of the oscillations is different from the undamped case.The frequency in this case is called the "damped natural frequency",
 and is related to the undamped natural frequency by the following formula:
and is related to the undamped natural frequency by the following formula:
The damped natural frequency is less than the undamped natural frequency, but for many practical cases the damping ratio is relatively small and hence the difference is negligible. Therefore the damped and undamped description are often dropped when stating the natural frequency (e.g. with 0.1 damping ratio, the damped natural frequency is only 1% less than the undamped).
The plots to the side present how 0.1 and 0.3 damping ratios effect how the system will “ring” down over time. What is often done in practice is to experimentally measure the free vibration after an impact (for example by a hammer) and then determine the natural frequency of the system by measuring the rate of oscillation as well as the damping ratio by measuring the rate of decay. The natural frequency and damping ratio are not only important in free vibration, but also characterize how a system will behave under forced vibration.
Forced vibration with damping
In this section we will see the behavior of the spring mass damper model when we add a harmonic force in the form below. A force of this type could, for example, be generated by a rotating imbalance.
If we again sum the forces on the mass we get the following ordinary differential equation:

The steady state
Steady state
A system in a steady state has numerous properties that are unchanging in time. This implies that for any property p of the system, the partial derivative with respect to time is zero:...
solution of this problem can be written as:

The result states that the mass will oscillate at the same frequency, f, of the applied force, but with a phase shift

The amplitude of the vibration “X” is defined by the following formula.

Where “r” is defined as the ratio of the harmonic force frequency over the undamped natural frequency of the mass–spring–damper model.

The phase shift ,
 is defined by the following formula.
is defined by the following formula.

 ) the amplitude of the vibration can get extremely high. This phenomenon is called resonance
) the amplitude of the vibration can get extremely high. This phenomenon is called resonanceMechanical resonance
Mechanical resonance is the tendency of a mechanical system to absorb more energy when the frequency of its oscillations matches the system's natural frequency of vibration than it does at other frequencies...
(subsequently the natural frequency of a system is often referred to as the resonant frequency). In rotor bearing systems any rotational speed that excites a resonant frequency is referred to as a critical speed
Critical speed
In solid mechanics, in the field of rotordynamics, the critical speed is the theoretical angular velocity which excites the natural frequency of a rotating object, such as a shaft, propeller, leadscrew, or gear. As the speed of rotation approaches the object's natural frequency, the object begins...
.
If resonance occurs in a mechanical system it can be very harmful – leading to eventual failure of the system. Consequently, one of the major reasons for vibration analysis is to predict when this type of resonance may occur and then to determine what steps to take to prevent it from occurring. As the amplitude plot shows, adding damping can significantly reduce the magnitude of the vibration. Also, the magnitude can be reduced if the natural frequency can be shifted away from the forcing frequency by changing the stiffness or mass of the system. If the system cannot be changed, perhaps the forcing frequency can be shifted (for example, changing the speed of the machine generating the force).
The following are some other points in regards to the forced vibration shown in the frequency response plots.
- At a given frequency ratio, the amplitude of the vibration, X, is directly proportional to the amplitude of the force
 (e.g. if you double the force, the vibration doubles)
(e.g. if you double the force, the vibration doubles) - With little or no damping, the vibration is in phase with the forcing frequency when the frequency ratio r < 1 and 180 degrees out of phase when the frequency ratio r > 1
- When r ≪ 1 the amplitude is just the deflection of the spring under the static force
 This deflection is called the static deflection
This deflection is called the static deflection  Hence, when r ≪ 1 the effects of the damper and the mass are minimal.
Hence, when r ≪ 1 the effects of the damper and the mass are minimal. - When r ≫ 1 the amplitude of the vibration is actually less than the static deflection
 In this region the force generated by the mass (F = ma) is dominating because the acceleration seen by the mass increases with the frequency. Since the deflection seen in the spring, X, is reduced in this region, the force transmitted by the spring (F = kx) to the base is reduced. Therefore the mass–spring–damper system is isolating the harmonic force from the mounting base – referred to as vibration isolationVibration isolationVibration isolation is the process of isolating an object, such as a piece of equipment, from the source of vibrations.-Passive isolation:Passive vibration isolation systems consist essentially of a mass, spring and damper ....
In this region the force generated by the mass (F = ma) is dominating because the acceleration seen by the mass increases with the frequency. Since the deflection seen in the spring, X, is reduced in this region, the force transmitted by the spring (F = kx) to the base is reduced. Therefore the mass–spring–damper system is isolating the harmonic force from the mounting base – referred to as vibration isolationVibration isolationVibration isolation is the process of isolating an object, such as a piece of equipment, from the source of vibrations.-Passive isolation:Passive vibration isolation systems consist essentially of a mass, spring and damper ....
. Interestingly, more damping actually reduces the effects of vibration isolation when r ≫ 1 because the damping force (F = cv) is also transmitted to the base.
What causes resonance?
Resonance is simple to understand if you view the spring and mass as energy storage elements – with the mass storing kinetic energy and the spring storing potential energy. As discussed earlier, when the mass and spring have no external force acting on them they transfer energy back and forth at a rate equal to the natural frequency. In other words, if energy is to be efficiently pumped into both the mass and spring the energy source needs to feed the energy in at a rate equal to the natural frequency. Applying a force to the mass and spring is similar to pushing a child on swing, you need to push at the correct moment if you want the swing to get higher and higher. As in the case of the swing, the force applied does not necessarily have to be high to get large motions; the pushes just need to keep adding energy into the system.The damper, instead of storing energy, dissipates energy. Since the damping force is proportional to the velocity, the more the motion, the more the damper dissipates the energy. Therefore a point will come when the energy dissipated by the damper will equal the energy being fed in by the force. At this point, the system has reached its maximum amplitude and will continue to vibrate at this level as long as the force applied stays the same. If no damping exists, there is nothing to dissipate the energy and therefore theoretically the motion will continue to grow on into infinity.
Applying "complex" forces to the mass–spring–damper model
In a previous section only a simple harmonic force was applied to the model, but this can be extended considerably using two powerful mathematical tools. The first is the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
that takes a signal as a function of time (time domain
Time domain
Time domain is a term used to describe the analysis of mathematical functions, physical signals or time series of economic or environmental data, with respect to time. In the time domain, the signal or function's value is known for all real numbers, for the case of continuous time, or at various...
) and breaks it down into its harmonic components as a function of frequency (frequency domain
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
). For example, let us apply a force to the mass–spring–damper model that repeats the following cycle – a force equal to 1 newton for 0.5 second and then no force for 0.5 second. This type of force has the shape of a 1 Hz square wave
Square wave
A square wave is a kind of non-sinusoidal waveform, most typically encountered in electronics and signal processing. An ideal square wave alternates regularly and instantaneously between two levels...
.

Frequency spectrum
The frequency spectrum of a time-domain signal is a representation of that signal in the frequency domain. The frequency spectrum can be generated via a Fourier transform of the signal, and the resulting values are usually presented as amplitude and phase, both plotted versus frequency.Any signal...
that presents the magnitude of the harmonics that make up the square wave (the phase is also generated, but is typically of less concern and therefore is often not plotted). The Fourier transform can also be used to analyze non-periodic
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
functions such as transients (e.g. impulses) and random functions. With the advent of the modern computer the Fourier transform is almost always computed using the Fast Fourier Transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT) computer algorithm in combination with a window function
Window function
In signal processing, a window function is a mathematical function that is zero-valued outside of some chosen interval. For instance, a function that is constant inside the interval and zero elsewhere is called a rectangular window, which describes the shape of its graphical representation...
.
In the case of our square wave force, the first component is actually a constant force of 0.5 newton and is represented by a value at "0" Hz in the frequency spectrum. The next component is a 1 Hz sine wave with an amplitude of 0.64. This is shown by the line at 1 Hz. The remaining components are at odd frequencies and it takes an infinite amount of sine waves to generate the perfect square wave. Hence, the Fourier transform allows you to interpret the force as a sum of sinusoidal forces being applied instead of a more "complex" force (e.g. a square wave).
In the previous section, the vibration solution was given for a single harmonic force, but the Fourier transform will in general give multiple harmonic forces. The second mathematical tool, "the principle of superposition"
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
, allows you to sum the solutions from multiple forces if the system is linear
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
. In the case of the spring–mass–damper model, the system is linear if the spring force is proportional to the displacement and the damping is proportional to the velocity over the range of motion of interest. Hence, the solution to the problem with a square wave is summing the predicted vibration from each one of the harmonic forces found in the frequency spectrum of the square wave.
Frequency response model
We can view the solution of a vibration problem as an input/output relation – where the force is the input and the output is the vibration. If we represent the force and vibration in the frequency domain (magnitude and phase) we can write the following relation:
 is called the frequency response
is called the frequency responseFrequency response
Frequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input...
function (also referred to as the transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
, but not technically as accurate) and has both a magnitude and phase component (if represented as a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, a real and imaginary component). The magnitude of the frequency response function (FRF) was presented earlier for the mass–spring–damper system.
 where
where 
The phase of the FRF was also presented earlier as:

For example, let us calculate the FRF for a mass–spring–damper system with a mass of 1 kg, spring stiffness of 1.93 N/mm and a damping ratio of 0.1. The values of the spring and mass give a natural frequency of 7 Hz for this specific system. If we apply the 1 Hz square wave from earlier we can calculate the predicted vibration of the mass. The figure illustrates the resulting vibration. It happens in this example that the fourth harmonic of the square wave falls at 7 Hz. The frequency response of the mass–spring–damper therefore outputs a high 7 Hz vibration even though the input force had a relatively low 7 Hz harmonic. This example highlights that the resulting vibration is dependent on both the forcing function and the system that the force is applied to.

The frequency response function (FRF) does not necessarily have to be calculated from the knowledge of the mass, damping, and stiffness of the system, but can be measured experimentally. For example, if you apply a known force and sweep the frequency and then measure the resulting vibration you can calculate the frequency response function and then characterize the system. This technique is used in the field of experimental modal analysis
Modal analysis
Modal analysis is the study of the dynamic properties of structures under vibrational excitation.Modal analysis is the field of measuring and analysing the dynamic response of structures and or fluids when excited by an input...
to determine the vibration characteristics of a structure.
Multiple degrees of freedom systems and mode shapes
The simple mass–spring damper model is the foundation of vibration analysis, but what about more complex systems? The mass–spring–damper model described above is called a single degree of freedomDegrees of freedom (engineering)
In mechanics, degrees of freedom are the set of independent displacements and/or rotations that specify completely the displaced or deformed position and orientation of the body or system...
(SDOF) model since we have assumed the mass only moves up and down. In the case of more complex systems we need to discretize the system into more masses and allow them to move in more than one direction – adding degrees of freedom. The major concepts of multiple degrees of freedom (MDOF) can be understood by looking at just a 2 degree of freedom model as shown in the figure.



We can rewrite this in matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
format:

A more compact form of this matrix equation can be written as:

where

 and
and  are symmetric matrices referred respectively as the mass, damping, and stiffness matrices. The matrices are NxN square matrices where N is the number of degrees of freedom of the system.
are symmetric matrices referred respectively as the mass, damping, and stiffness matrices. The matrices are NxN square matrices where N is the number of degrees of freedom of the system.In the following analysis we will consider the case where there is no damping and no applied forces (i.e. free vibration). The solution of a viscously damped system is somewhat more complicated.

This differential equation can be solved by assuming the following type of solution:

Note: Using the exponential solution of
 is a mathematical trick used to solve linear differential equations. If we use Euler's formula
is a mathematical trick used to solve linear differential equations. If we use Euler's formulaEuler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
and take only the real part of the solution it is the same cosine solution for the 1 DOF system. The exponential solution is only used because it easier to manipulate mathematically.
The equation then becomes:

Since
 cannot equal zero the equation reduces to the following.
cannot equal zero the equation reduces to the following.
Eigenvalue problem
This is referred to an eigenvalue problem in mathematics and can be put in the standard format by pre-multiplying the equation by

and if we let
 and
and 

The solution to the problem results in N eigenvalues (i.e.
 ), where N corresponds to the number of degrees of freedom. The eigenvalues provide the natural frequencies of the system. When these eigenvalues are substituted back into the original set of equations, the values of
), where N corresponds to the number of degrees of freedom. The eigenvalues provide the natural frequencies of the system. When these eigenvalues are substituted back into the original set of equations, the values of  that correspond to each eigenvalue are called the eigenvectors. These eigenvectors represent the mode shapes of the system. The solution of an eigenvalue problem can be quite cumbersome (especially for problems with many degrees of freedom), but fortunately most math analysis programs have eigenvalue routines.
that correspond to each eigenvalue are called the eigenvectors. These eigenvectors represent the mode shapes of the system. The solution of an eigenvalue problem can be quite cumbersome (especially for problems with many degrees of freedom), but fortunately most math analysis programs have eigenvalue routines.The eigenvalues and eigenvectors are often written in the following matrix format and describe the modal model of the system:
 and
and 
A simple example using our 2 DOF model can help illustrate the concepts. Let both masses have a mass of 1 kg and the stiffness of all three springs equal 1000 N/m. The mass and stiffness matrix for this problem are then:
 and
and 
Then

The eigenvalues for this problem given by an eigenvalue routine will be:

The natural frequencies in the units of hertz are then (remembering
 )
)  and
and  .
.The two mode shapes for the respective natural frequencies are given as:

Since the system is a 2 DOF system, there are two modes with their respective natural frequencies and shapes. The mode shape vectors are not the absolute motion, but just describe relative motion of the degrees of freedom. In our case the first mode shape vector is saying that the masses are moving together in phase since they have the same value and sign. In the case of the second mode shape vector, each mass is moving in opposite direction at the same rate.
Illustration of a multiple DOF problem
When there are many degrees of freedom, the best method of visualizing the mode shapes is by animating them. An example of animated mode shapes is shown in the figure below for a cantileverCantilever
A cantilever is a beam anchored at only one end. The beam carries the load to the support where it is resisted by moment and shear stress. Cantilever construction allows for overhanging structures without external bracing. Cantilevers can also be constructed with trusses or slabs.This is in...
ed I-beam
I-beam
-beams, also known as H-beams, W-beams , rolled steel joist , or double-T are beams with an - or H-shaped cross-section. The horizontal elements of the "" are flanges, while the vertical element is the web...
. In this case, a finite element
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
model was used to generate the mass and stiffness matrices and solve the eigenvalue problem. Even this relatively simple model has over 100 degrees of freedom and hence as many natural frequencies and mode shapes. In general only the first few modes are important.
The mode shapes of a cantilevered I-beam
Multiple DOF problem converted to a single DOF problem
The eigenvectors have very important properties called orthogonality properties. These properties can be used to greatly simplify the solution of multi-degree of freedom models. It can be shown that the eigenvectors have the following properties:

 and
and  are diagonal matrices
are diagonal matricesDiagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
that contain the modal mass and stiffness values for each one of the modes. (Note: Since the eigenvectors (mode shapes) can be arbitrarily scaled, the orthogonality properties are often used to scale the eigenvectors so the modal mass value for each mode is equal to 1. The modal mass matrix is therefore an identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
)
These properties can be used to greatly simplify the solution of multi-degree of freedom models by making the following coordinate transformation.

If we use this coordinate transformation in our original free vibration differential equation we get the following equation.

We can take advantage of the orthogonality properties by premultiplying this equation by


The orthogonality properties then simplify this equation to:

This equation is the foundation of vibration analysis for multiple degree of freedom systems. A similar type of result can be derived for damped systems. The key is that the modal and stiffness matrices are diagonal matrices and therefore we have "decoupled" the equations. In other words, we have transformed our problem from a large unwieldy multiple degree of freedom problem into many single degree of freedom problems that can be solved using the same methods outlined above.
Instead of solving for x we are instead solving for q, referred to as the modal coordinates or modal participation factors.
It may be clearer to understand if we write
 as:
as:
Written in this form we can see that the vibration at each of the degrees of freedom is just a linear sum of the mode shapes. Furthermore, how much each mode "participates" in the final vibration is defined by q, its modal participation factor.
See also
- Balancing machineBalancing MachineA balancing machine is a measuring tool used for balancing rotating machine parts such as rotors for electric motors, fans, turbines, disc brakes, disc drives, propellers and pumps. The machine usually consists of two rigid pedestals, with suspension and bearings on top supporting a mounting...
- Base isolationBase isolationBase isolation, also known as seismic base isolation or base isolation system, is one of the most popular means of protecting a structure against earthquake forces...
- CushioningCushioningPackage cushioning is used to help protect fragile items during shipment. It is common for a transport package to be dropped, kicked, and impacted: These events may produce potentially damaging shocks. Transportation vibration from conveyors, trucks, railroads, or aircraft can also damage some...
- Critical speedCritical speedIn solid mechanics, in the field of rotordynamics, the critical speed is the theoretical angular velocity which excites the natural frequency of a rotating object, such as a shaft, propeller, leadscrew, or gear. As the speed of rotation approaches the object's natural frequency, the object begins...
- DampingDampingIn physics, damping is any effect that tends to reduce the amplitude of oscillations in an oscillatory system, particularly the harmonic oscillator.In mechanics, friction is one such damping effect...
- Dunkerley's MethodDunkerley's MethodDunkerley's method is used in mechanical engineering to determine the critical speed of a shaft-rotor system. Other methods include the Rayleigh–Ritz method.-Whirling of a shaft:...
- Earthquake engineeringEarthquake engineeringEarthquake engineering is the scientific field concerned with protecting society, the natural and the man-made environment from earthquakes by limiting the seismic risk to socio-economically acceptable levels...
- Fast Fourier transformFast Fourier transformA fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
- Journal of Sound and VibrationJournal of Sound and VibrationThe Journal of Sound and Vibration is a scientific journal in the field of acoustics. It is published by Elsevier.-External links:*...
- Mechanical resonanceMechanical resonanceMechanical resonance is the tendency of a mechanical system to absorb more energy when the frequency of its oscillations matches the system's natural frequency of vibration than it does at other frequencies...
- Modal analysisModal analysisModal analysis is the study of the dynamic properties of structures under vibrational excitation.Modal analysis is the field of measuring and analysing the dynamic response of structures and or fluids when excited by an input...
- Mode shape
- Noise and vibration on maritime vesselsNoise and vibration on maritime vesselsNoise and vibration on maritime vessels are not the same but they have the same origin and come in many forms. The methods to handle the related problems are similar, to a certain level, where most shipboard noise problems are reduced by controlling vibration....
- Noise, Vibration, and HarshnessNoise, Vibration, and HarshnessNoise, vibration, and harshness , also known as noise and vibration , is the study and modification of the noise and vibration characteristics of vehicles, particularly cars and trucks...
- Quantum vibration
- Random vibrationRandom vibrationIn mechanical engineering, random vibration is motion which is non-deterministic, meaning that future behavior cannot be precisely predicted. The randomness is a characteristic of the excitation or input, not the mode shapes or natural frequencies...
- Ride qualityRide qualityRide quality refers to the degree of protection offered vehicle occupants from uneven elements in the road surface, or the terrain if driving off-road. A car with very good ride quality is also a comfortable car to ride in. Cars which disturb vehicle occupants with major or minor road...
- ShockShock (mechanics)A mechanical or physical shock is a sudden acceleration or deceleration caused, for example, by impact, drop, kick, earthquake, or explosion. Shock is a transient physical excitation....
- Simple harmonic oscillator
- SoundSoundSound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
- Structural acousticsStructural acousticsStructural acoustics is the study of the mechanical waves in structures and how they interact with and radiate into adjacent fluids. The field of structural acoustics is often referred to as vibroacoustics in Europe and Asia. People that work in the field of structural acoustics are known as...
- Structural dynamicsStructural DynamicsStructural dynamics is a subset of structural analysis which covers the behaviour of structures subjected to dynamic loading. Dynamic loads include people, wind, waves, traffic, earthquakes, and blasts. Any structure can be subject to dynamic loading. Dynamic analysis can be used to find dynamic...
- Tire balanceTire balanceTire balance, also referred to as tire unbalance or imbalance, describes the distribution of mass within an automobile tire or the wheel to which it is attached. When the tire rotates, asymmetries of mass cause the wheel to wobble, which can cause ride disturbances, usually vertical and lateral...
- Torsional vibrationTorsional vibrationTorsional vibration is angular vibration of an object—commonly a shaft along its axis of rotation. Torsional vibration is often a concern in power transmission systems using rotating shafts or couplings where it can cause failures if not controlled....
- Vibration controlVibration controlIn earthquake engineering, vibration control is a set of technical means aimed to mitigate seismic impacts in building and non-building structures.All seismic vibration control devices may be classified as passive, active or hybrid where:...
- Vibration isolationVibration isolationVibration isolation is the process of isolating an object, such as a piece of equipment, from the source of vibrations.-Passive isolation:Passive vibration isolation systems consist essentially of a mass, spring and damper ....
- Vibration of rotating structuresVibration of rotating structures- Vibration of Rotating Structures : =M*V*\ddot sE+B*V*\dot sE+pE pU=A*V*\dot sU M,D,K classical matrices: mass matrix, damping matrix and stiffness matrix G gyroscopic matrix of vibration velocity...
- WaveWaveIn physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
- Whole body vibrationWhole body vibrationWhole body vibration , as a therapy, was explored by Russian scientist Vladimir Nazarov, who tested vibration on cosmonauts in an effort to decrease the loss of muscle and bone mass in space. As there is minimal gravitational force in space, muscles and bones are not loaded as they normally are on...
Further reading
- Tongue, Benson, Principles of Vibration, Oxford University Press, 2001, ISBN 0-195-142462
- Inman, Daniel J., Engineering Vibration, Prentice Hall, 2001, ISBN 013726142X
- Rao, Singiresu, Mechanical Vibrations, Addison Wesley, 1990, ISBN 0-201-50156-2
- Thompson, W.T., Theory of Vibrations, Nelson Thornes Ltd, 1996, ISBN 0-412-783908
- Hartog, Den, Mechanical Vibrations, Dover Publications, 1985, ISBN 0-486-647854
External links
- Hyperphysics Educational Website, Concepts
- Nelson Publishing, Evaluation Engineering Magazine
- Structural Dynamics and Vibration Laboratory of McGill University
- Normal vibration modes of a circular membrane
- Free Excel sheets to estimate modal parameters