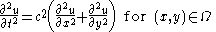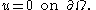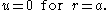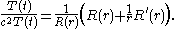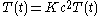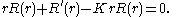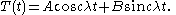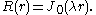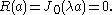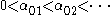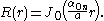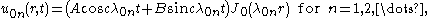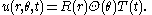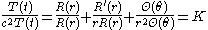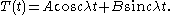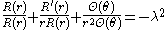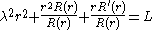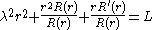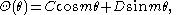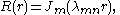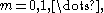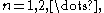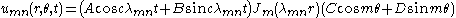Vibrations of a circular drum
Encyclopedia
Vibration
Vibration refers to mechanical oscillations about an equilibrium point. The oscillations may be periodic such as the motion of a pendulum or random such as the movement of a tire on a gravel road.Vibration is occasionally "desirable"...
s of an idealized circular drum
Drum
The drum is a member of the percussion group of musical instruments, which is technically classified as the membranophones. Drums consist of at least one membrane, called a drumhead or drum skin, that is stretched over a shell and struck, either directly with the player's hands, or with a...
, essentially an elastic membrane
Acoustic membrane
An acoustic membrane is a thin layer that vibrates and are used in acoustics to produce or transfer sound, such as a drum, microphone, or loudspeaker....
of uniform thickness attached to a rigid circular frame, are solutions of the wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
with zero boundary conditions.
There exist infinitely many ways in which a drum can vibrate, depending on the shape of the drum at some initial time and the rate of change
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the shape of the drum at the initial time. Using separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
, it is possible to find a collection of "simple" vibration modes, and it can be proved that any arbitrarily complex vibration of a drum can be decomposed as a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
of the simpler vibrations (analogously to the Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
).
Motivation
Analyzing the vibrating drum problem explains percussion instruments such as drumDrum
The drum is a member of the percussion group of musical instruments, which is technically classified as the membranophones. Drums consist of at least one membrane, called a drumhead or drum skin, that is stretched over a shell and struck, either directly with the player's hands, or with a...
s and timpani
Timpani
Timpani, or kettledrums, are musical instruments in the percussion family. A type of drum, they consist of a skin called a head stretched over a large bowl traditionally made of copper. They are played by striking the head with a specialized drum stick called a timpani stick or timpani mallet...
. However, there is also a biological application in the working of the eardrum
Eardrum
The eardrum, or tympanic membrane, is a thin membrane that separates the external ear from the middle ear in humans and other tetrapods. Its function is to transmit sound from the air to the ossicles inside the middle ear. The malleus bone bridges the gap between the eardrum and the other ossicles...
. From an educational point of view the modes of a two-dimensional object are a convenient way to visually demonstrate the meaning of modes, nodes, antinodes and even quantum number
Quantum number
Quantum numbers describe values of conserved quantities in the dynamics of the quantum system. Perhaps the most peculiar aspect of quantum mechanics is the quantization of observable quantities. This is distinguished from classical mechanics where the values can range continuously...
s. These concepts are important to the understanding of the structure of the atom.
The problem
Consider an open disk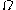 of radius
of radius  centered at the origin, which will represent the "still" drum shape. At any time
centered at the origin, which will represent the "still" drum shape. At any time 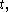 the height of the drum shape at a point
the height of the drum shape at a point 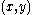 in
in 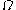 measured from the "still" drum shape will be denoted by
measured from the "still" drum shape will be denoted by 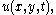 which can take both positive and negative values. Let
which can take both positive and negative values. Let 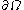 denote the boundary
denote the boundaryBoundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of
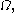 that is, the circle of radius
that is, the circle of radius  centered at the origin, which represents the rigid frame to which the drum is attached.
centered at the origin, which represents the rigid frame to which the drum is attached.The mathematical equation that governs the vibration of the drum is the wave equation with zero boundary conditions,
Here,
 is a positive constant, which gives the "speed" of vibration.
is a positive constant, which gives the "speed" of vibration.Due to the circular geometry of
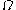 , it will be convenient to use cylindrical coordinates,
, it will be convenient to use cylindrical coordinates, 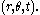 Then, the above equations are written as
Then, the above equations are written as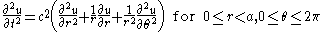
The radially symmetric case
We will first study the possible modes of vibration of a circular drum that are radially symmetric. Then, the function does not depend on the angle
does not depend on the angle 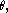 and the wave equation simplifies to
and the wave equation simplifies to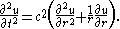
We will look for solutions in separated variables,
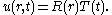 Substituting this in the equation above and dividing both sides by
Substituting this in the equation above and dividing both sides by 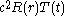 yields
yieldsThe left-hand side of this equality does not depend on
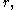 and the right-hand side does not depend on
and the right-hand side does not depend on 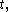 it follows that both sides must equal to some constant
it follows that both sides must equal to some constant 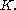 We get separate equations for
We get separate equations for 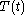 and
and 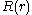 :
:The equation for
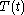 has solutions which exponentially grow or decay for
has solutions which exponentially grow or decay for 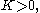 are linear or constant for
are linear or constant for 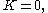 and are periodic for
and are periodic for 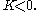 Physically it is expected that a solution to the problem of a vibrating drum will be oscillatory in time, and this leaves only the third case,
Physically it is expected that a solution to the problem of a vibrating drum will be oscillatory in time, and this leaves only the third case, 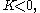 when
when 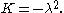 Then,
Then, 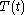 is a linear combination of sine and cosine functions,
is a linear combination of sine and cosine functions,Turning to the equation for
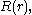 with the observation that
with the observation that 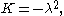 all solutions of this second-order differential equation are a linear combination of Bessel function
all solutions of this second-order differential equation are a linear combination of Bessel functionBessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
s of order 0,
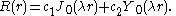
The Bessel function
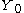 is unbounded for
is unbounded for 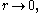 which results in an unphysical solution to the vibrating drum problem, so the constant
which results in an unphysical solution to the vibrating drum problem, so the constant 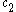 must be null. We will also assume
must be null. We will also assume 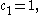 as otherwise this constant can be absorbed later into the constants
as otherwise this constant can be absorbed later into the constants 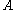 and
and 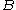 coming from
coming from 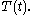 It follows that
It follows thatThe requirement that height
 be zero on the boundary of the drum results in the condition
be zero on the boundary of the drum results in the conditionThe Bessel function
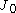 has an infinite number of positive roots,
has an infinite number of positive roots,We get that
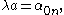 for
for 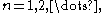 so
soTherefore, the radially symmetric solutions
 of the vibrating drum problem that can be represented in separated variables are
of the vibrating drum problem that can be represented in separated variables arewhere
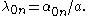
The general case
The general case, when can also depend on the angle
can also depend on the angle 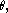 is treated similarly. We assume a solution in separated variables,
is treated similarly. We assume a solution in separated variables,Substituting this into the wave equation and separating the variables, gives
where
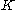 is a constant. As before, from the equation for
is a constant. As before, from the equation for 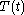 it follows that
it follows that 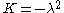 with
with 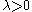 and
andFrom the equation
we obtain, by multiplying both sides by
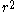 and separating variables, that
and separating variables, thatand
for some constant
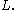 Since
Since 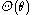 is periodic, with period
is periodic, with period 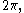
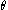 being an angular variable, it follows that
being an angular variable, it follows thatwhere
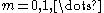 and
and 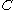 and
and 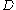 are some constants. This also implies
are some constants. This also implies 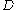
Going back to the equation for
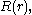 its solution is a linear combination of Bessel function
its solution is a linear combination of Bessel functionBessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
s
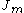 and
and 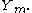 With a similar argument as in the previous section, we arrive at
With a similar argument as in the previous section, we arrive atwhere
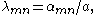 with
with 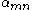 the
the  -th positive root of
-th positive root of 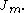
We showed that all solutions in separated variables of the vibrating drum problem are of the form
for
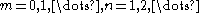
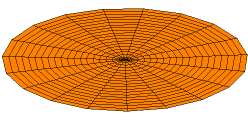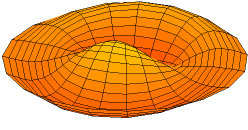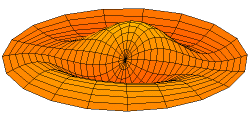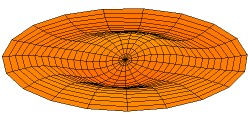
Animations of several vibration modes
A number of modes are shown below together with their quantum numbers. The analogous wave functions of the hydrogen atom are also indicated as well as the associated angular frequency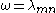 .
.