
Von Neumann's theorem
Encyclopedia
In mathematics
, von Neumann's theorem is a result in the operator theory
of linear operators on Hilbert space
s.
from G into H. Let T∗ : dom(T∗) ⊆ H → G denote the Hilbert adjoint of T. Suppose that T is a closed operator
and that T is densely defined, i.e. dom(T) is dense in G. Then T∗T is also densely defined and self-adjoint
. That is,
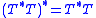
and the operators on the right- and let-hand sides have the same dense domain in G.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, von Neumann's theorem is a result in the operator theory
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
of linear operators on Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s.
Statement of the theorem
Let G and H be Hilbert spaces, and let T : dom(T) ⊆ G → H be a densely-defined operatorDensely-defined operator
In mathematics — specifically, in operator theory — a densely defined operator is a type of partially defined function; in a topological sense, it is a linear operator that is defined "almost everywhere"...
from G into H. Let T∗ : dom(T∗) ⊆ H → G denote the Hilbert adjoint of T. Suppose that T is a closed operator
Closed operator
In mathematics, specifically in functional analysis, closed linear operators are an important class of linear operators on Banach spaces. They are more general than bounded operators, and therefore not necessarily continuous, but they still retain nice enough properties that one can define the...
and that T is densely defined, i.e. dom(T) is dense in G. Then T∗T is also densely defined and self-adjoint
Self-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
. That is,
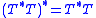
and the operators on the right- and let-hand sides have the same dense domain in G.

