Wannier function
Encyclopedia
The Wannier functions are a complete set of orthogonal functions
used in solid-state physics
. They were introduced by Gregory Wannier
.
The Wannier functions for different lattice sites in a crystal
are orthogonal, allowing a convenient basis for the expansion of electron
states in certain regimes. Wannier functions have found widespread use, for example, in the analysis of binding forces acting on electrons; they have proven to be in general localized, at least for insulators, in 2006. Specifically, these functions are also used in the analysis of exciton
s and condensed Rydberg matter
.
in a perfect crystal, and denote its Bloch states by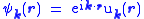
where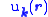
has the same periodicity as the crystal. Then the Wannier functions are defined by
,
where
where "BZ" denotes the Brillouin zone, which has volume Ω.
In other words, a Wannier function only depends on the quantity (r-R). As a result, these functions are often written in the alternative notation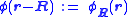
where the sum is over each lattice vector R in the crystal.
Wannier functions have been extended to nearly periodic potentials as well.
are defined as the eigenfunctions of a particular Hamiltonian, and are therefore defined only up to an overall phase. By applying a phase transformation 
to the functions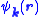 
, for any (real) function 
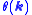, one arrives at an equally valid choice. While the change has no consequences for the properties of the Bloch states, the corresponding Wannier functions are significantly changed by this transformation.
One therefore uses the freedom to choose the phases of the Bloch states in order to give the most convenient set of Wannier functions. In practice, this is usually the maximally-localized set, in which the Wannier function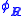
is localized around the point R and rapidly goes to zero away from R. For the one-dimensional case, it has been proved by Kohn that there is always a unique choice that gives these properties (subject to certain symmetries). This consequently applies to any separable potential
in higher dimensions; the general conditions are not established, and are the subject of ongoing research.
in crystals, for example, ferroelectrics
. See for example, Berghold, and Nakhmanson., and a power-point introduction by Vanderbilt The polarization per unit cell in a solid can be defined as the dipole moment of the Wannier charge density: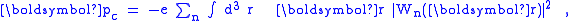
where the summation is over the occupied bands, and Wn is the Wannier function localized in the cell for band n. The change in polarization during a continuous physical process is the time derivative of the polarization and also can be formulated in terms of the Berry phase of the occupied Bloch states.
Orthogonal functions
In mathematics, two functions f and g are called orthogonal if their inner product \langle f,g\rangle is zero for f ≠ g. Whether or not two particular functions are orthogonal depends on how their inner product has been defined. A typical definition of an inner product for functions is...
used in solid-state physics
Solid-state physics
Solid-state physics is the study of rigid matter, or solids, through methods such as quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from...
. They were introduced by Gregory Wannier
Gregory Wannier
Gregory Hugh Wannier was a Swiss physicist.He attended Princeton as a graduate student and later taught at several American universities before a stint in industry....
.
The Wannier functions for different lattice sites in a crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
are orthogonal, allowing a convenient basis for the expansion of electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
states in certain regimes. Wannier functions have found widespread use, for example, in the analysis of binding forces acting on electrons; they have proven to be in general localized, at least for insulators, in 2006. Specifically, these functions are also used in the analysis of exciton
Exciton
An exciton is a bound state of an electron and hole which are attracted to each other by the electrostatic Coulomb force. It is an electrically neutral quasiparticle that exists in insulators, semiconductors and some liquids...
s and condensed Rydberg matter
Rydberg matter
Rydberg matter is a phase of matter formed by Rydberg atoms; it was predicted around 1980 by É. A. Manykin, M. I. Ozhovan and P. P. Poluéktov. It has been formed from various elements like caesium, potassium, hydrogen and nitrogen; studies have been conducted on theoretical possibilities like...
.
Definition
Although Wannier functions can be chosen in many different ways, the original, simplest, and most common definition in solid-state physics is as follows. Choose a single bandElectronic band structure
In solid-state physics, the electronic band structure of a solid describes those ranges of energy an electron is "forbidden" or "allowed" to have. Band structure derives from the diffraction of the quantum mechanical electron waves in a periodic crystal lattice with a specific crystal system and...
in a perfect crystal, and denote its Bloch states by
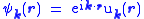
where
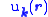has the same periodicity as the crystal. Then the Wannier functions are defined by,where
- R is any lattice vector (i.e., there is one Wannier function for each Bravais lattice vector);
- N is the number of primitive cellPrimitive cellUsed predominantly in geometry, solid state physics, and mineralogy, particularly in describing crystal structure, a primitive cell is a minimum cell corresponding to a single lattice point of a structure with translational symmetry in 2 dimensions, 3 dimensions, or other dimensions...
s in the crystal; - The sum on k includes all the values of k in the Brillouin zoneBrillouin zoneIn mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
(or any other primitive cellPrimitive cellUsed predominantly in geometry, solid state physics, and mineralogy, particularly in describing crystal structure, a primitive cell is a minimum cell corresponding to a single lattice point of a structure with translational symmetry in 2 dimensions, 3 dimensions, or other dimensions...
of the reciprocal latticeReciprocal latticeIn physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
) that are consistent with periodic boundary conditionsPeriodic boundary conditionsIn mathematical models and computer simulations, periodic boundary conditions are a set of boundary conditions that are often used to simulate a large system by modelling a small part that is far from its edge...
on the crystal. This includes N different values of k, spread out uniformly through the Brillouin zone. Since N is usually very large, the sum can be written as an integral according to the replacement rule:
where "BZ" denotes the Brillouin zone, which has volume Ω.
Properties
On the basis of this definition, the following properties can be proven to hold:- For any lattice vector R' ,
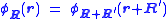
In other words, a Wannier function only depends on the quantity (r-R). As a result, these functions are often written in the alternative notation
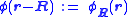
- The Bloch functions can be written in terms of Wannier functions as follows:
,
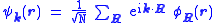where the sum is over each lattice vector R in the crystal.
- The set of wavefunctions
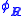is an orthonormal basisOrthonormal basisIn mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
for the band in question.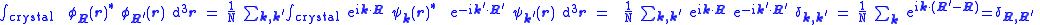
Wannier functions have been extended to nearly periodic potentials as well.
Localization
The Bloch states are defined as the eigenfunctions of a particular Hamiltonian, and are therefore defined only up to an overall phase. By applying a phase transformation to the functions 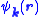, for any (real) function 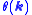, one arrives at an equally valid choice. While the change has no consequences for the properties of the Bloch states, the corresponding Wannier functions are significantly changed by this transformation.One therefore uses the freedom to choose the phases of the Bloch states in order to give the most convenient set of Wannier functions. In practice, this is usually the maximally-localized set, in which the Wannier function
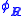is localized around the point R and rapidly goes to zero away from R. For the one-dimensional case, it has been proved by Kohn that there is always a unique choice that gives these properties (subject to certain symmetries). This consequently applies to any separable potentialSeparable partial differential equation
A separable partial differential equation is one that can be broken into a set of separate equations of lower dimensionality by a method of separation of variables. This generally relies upon the problem having some special form or symmetry...
in higher dimensions; the general conditions are not established, and are the subject of ongoing research.
Modern theory of polarization
Wannier functions have recently found application in describing the polarizationPolarization density
In classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is...
in crystals, for example, ferroelectrics
Ferroelectricity
Ferroelectricity is a property of certain materials which possess a spontaneous electric polarization that can be reversed by the application of an external electric field. The term is used in analogy to ferromagnetism, in which a material exhibits a permanent magnetic moment. Ferromagnetism was...
. See for example, Berghold, and Nakhmanson., and a power-point introduction by Vanderbilt The polarization per unit cell in a solid can be defined as the dipole moment of the Wannier charge density:
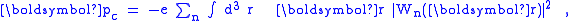
where the summation is over the occupied bands, and Wn is the Wannier function localized in the cell for band n. The change in polarization during a continuous physical process is the time derivative of the polarization and also can be formulated in terms of the Berry phase of the occupied Bloch states.
External links
- "The structure of electronic excitation levels in insulating crystals," G. H. Wannier, Phys. Rev. 52, 191 (1937)
- Wannier90 computer code that calculates maximally localized Wannier functions
- Wannier Transport code that calculates maximally localized Wannier functions fit for Quantum Transport applications