Watterson estimator
Encyclopedia
In population genetics
, the Watterson estimator is a method for estimating the population mutation rate,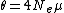
, where 
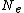is the effective population size
and
is the per-generation mutation rate
of the population of interest . The assumptions made are that there is a sample of n haploid individuals from the population of interest, that there are infinitely many sites capable of varying (so that mutations never overlay or reverse one another), and that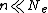
.
The estimate of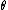
, often denoted as 
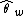, is
Population genetics
Population genetics is the study of allele frequency distribution and change under the influence of the four main evolutionary processes: natural selection, genetic drift, mutation and gene flow. It also takes into account the factors of recombination, population subdivision and population...
, the Watterson estimator is a method for estimating the population mutation rate,
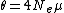, where 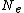is the effective population sizeEffective population size
In population genetics, the concept of effective population size Ne was introduced by the American geneticist Sewall Wright, who wrote two landmark papers on it...
and
is the per-generation mutation rateMutation rate
In genetics, the mutation rate is the chance of a mutation occurring in an organism or gene in each generation...
of the population of interest . The assumptions made are that there is a sample of n haploid individuals from the population of interest, that there are infinitely many sites capable of varying (so that mutations never overlay or reverse one another), and that
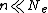.The estimate of
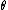, often denoted a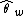s , is-
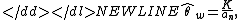
where K is the number of segregating sites (an example of a segregating site would be a single-nucleotide polymorphism) in the sample and
-
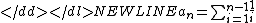
is the (n − 1)th harmonic number.
This estimate is based on coalescent theoryCoalescent theoryIn genetics, coalescent theory is a retrospective model of population genetics. It attempts to trace all alleles of a gene shared by all members of a population to a single ancestral copy, known as the most recent common ancestor...
. Watterson's estimator is commonly used for its simplicity. When its assumptions are met, the estimator is unbiasedBias of an estimatorIn statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
and the varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the estimator decreases with increasing sample size or recombination rate. However, the estimator can be biased by population structure. For example,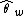
is downwardly biased in an exponentially growingExponential growthExponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
population. It can also be biased by violation of the infinite-sites mutational model; if multiple mutations can overwrite one another, Watterson's estimator will be biased downward.
See also
- Tajima's DTajima's DTajima's D is a statistical test created by and named after the Japanese researcher Fumio Tajima. The purpose of the test is to distinguish between a DNA sequence evolving randomly and one evolving under a non-random process, including directional selection or balancing selection, demographic...
- Fu estimator
- Coupon collector's problemCoupon collector's problemIn probability theory, the coupon collector's problem describes the "collect all coupons and win" contests. It asks the following question: Suppose that there are n coupons, from which coupons are being collected with replacement...
- Ewens sampling formula
- Tajima's D
-