Coalescent theory
Encyclopedia
In genetics
, coalescent theory is a retrospective model of population genetics. It attempts to trace all allele
s of a gene
shared by all members of a population to a single ancestral copy, known as the most recent common ancestor
(MRCA; sometimes also termed the coancestor to emphasize the coalescent relationship). The inheritance relationships between alleles are typically represented as a gene genealogy, similar in form to a phylogenetic tree
. This gene genealogy is also known as the coalescent; understanding the statistical properties of the coalescent under different assumptions forms the basis of coalescent theory.
The coalescent runs models of genetic drift
backward in time to investigate the genealogy
of antecedents
. In the most simple case, coalescent theory assumes no recombination
, no natural selection
, and no gene flow
or population structure. Advances in coalescent theory, however, allow extension to the basic coalescent, and can include recombination, selection, and virtually any arbitrarily complex evolutionary or demographic model in population genetic analysis. The mathematical theory of the coalescent was originally developed in the early 1980s by John Kingman
.
. By tracing the ancestry of these two individuals backwards there will be a point in time when the MRCA is encountered and the two lineages will have coalesced.
The probability that two lineage
s coalesce in the immediately preceding generation is the probability that they share a parent. In a diploid population with a constant effective population size
with 2Ne copies of each locus, there are 2Ne "potential parents" in the previous generation, so the probability that two alleles share a parent is 1/(2Ne) and correspondingly, the probability that they do not coalesce is 1 − 1/(2Ne).
At each successive preceding generation, the probability of coalescence is geometrically distributed — that is, it is the probability of noncoalescence at the t − 1 preceding generations multiplied by the probability of coalescence at the generation of interest:
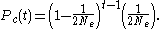
For sufficiently large values of Ne, this distribution is well approximated by the continuously defined exponential distribution
The standard exponential distribution has both the expected value
and the standard deviation
equal to 2Ne; therefore, although the expected time to coalescence is 2Ne, actual coalescence times have a wide range of variation. Note that coalescent time is the number of preceding generations where the coalescence took place and not calendar time though an estimation of the latter can be made multiplying 2Ne with the average time between generations.
sequences expected from genetic drift alone. This value is termed the mean heterozygosity, represented as
. Mean heterozygosity is calculated as the probability of a mutation occurring at a given generation divided by the probability of any "event" at that generation (either a mutation or a coalescence). The probability that the event is a mutation is the probability of a mutation in either of the two lineages: 
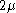. Thus the mean heterozygosity is equal to
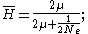
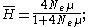
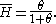
For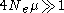
, the vast majority of allele pairs have at least one difference in nucleotide
sequence.
s which show the relationship of branches of the population to each other. The point where two branches meet indicates a coalescent event.
concept of neutral evolution and is an approximation to the Fisher-Wright (or Wright-Fisher) model for large populations. It was ‘discovered’ independently by several researchers in the 1980’s , but the definitive formalisation is attributed to Kingman . Major contributions to the development of coalescent theory have been made by Peter Donnelly
, Robert Griffiths
, Richard R Hudson and Simon Tavaré. This has included incorporating variations in population size, recombination and selection. In 1999 Jim Pitman and Serik Sagitov independently introduced coalescent processes with multiple collisions of ancestral lineages. Shortly later the full class of exchangeable coalescent processes with simultaneous multiple mergers of ancestral lineages was discovered by Martin Möhle and Serik Sagitov and Jason Schweinsberg.
Genetics
Genetics , a discipline of biology, is the science of genes, heredity, and variation in living organisms....
, coalescent theory is a retrospective model of population genetics. It attempts to trace all allele
Allele
An allele is one of two or more forms of a gene or a genetic locus . "Allel" is an abbreviation of allelomorph. Sometimes, different alleles can result in different observable phenotypic traits, such as different pigmentation...
s of a gene
Gene
A gene is a molecular unit of heredity of a living organism. It is a name given to some stretches of DNA and RNA that code for a type of protein or for an RNA chain that has a function in the organism. Living beings depend on genes, as they specify all proteins and functional RNA chains...
shared by all members of a population to a single ancestral copy, known as the most recent common ancestor
Most recent common ancestor
In genetics, the most recent common ancestor of any set of organisms is the most recent individual from which all organisms in the group are directly descended...
(MRCA; sometimes also termed the coancestor to emphasize the coalescent relationship). The inheritance relationships between alleles are typically represented as a gene genealogy, similar in form to a phylogenetic tree
Phylogenetic tree
A phylogenetic tree or evolutionary tree is a branching diagram or "tree" showing the inferred evolutionary relationships among various biological species or other entities based upon similarities and differences in their physical and/or genetic characteristics...
. This gene genealogy is also known as the coalescent; understanding the statistical properties of the coalescent under different assumptions forms the basis of coalescent theory.
The coalescent runs models of genetic drift
Genetic drift
Genetic drift or allelic drift is the change in the frequency of a gene variant in a population due to random sampling.The alleles in the offspring are a sample of those in the parents, and chance has a role in determining whether a given individual survives and reproduces...
backward in time to investigate the genealogy
Genealogy
Genealogy is the study of families and the tracing of their lineages and history. Genealogists use oral traditions, historical records, genetic analysis, and other records to obtain information about a family and to demonstrate kinship and pedigrees of its members...
of antecedents
Antecedent (genealogy)
In genealogy or in phylogenetic studies of evolutionary biology an antecedent, antecessor or antecedents are predecessors in a family line. I am the descendants of my grandparents, they are my antecedents. This term has particular utility in evolutionary coalescent theory, which models the process...
. In the most simple case, coalescent theory assumes no recombination
Genetic recombination
Genetic recombination is a process by which a molecule of nucleic acid is broken and then joined to a different one. Recombination can occur between similar molecules of DNA, as in homologous recombination, or dissimilar molecules, as in non-homologous end joining. Recombination is a common method...
, no natural selection
Natural selection
Natural selection is the nonrandom process by which biologic traits become either more or less common in a population as a function of differential reproduction of their bearers. It is a key mechanism of evolution....
, and no gene flow
Gene flow
In population genetics, gene flow is the transfer of alleles of genes from one population to another.Migration into or out of a population may be responsible for a marked change in allele frequencies...
or population structure. Advances in coalescent theory, however, allow extension to the basic coalescent, and can include recombination, selection, and virtually any arbitrarily complex evolutionary or demographic model in population genetic analysis. The mathematical theory of the coalescent was originally developed in the early 1980s by John Kingman
John Kingman
Sir John Frank Charles Kingman, born on 28 August 1939 in Beckenham, Kent, is a British mathematician.He was N. M. Rothschild and Sons Professor of Mathematical Sciences and Director of the Isaac Newton Institute at the University of Cambridge from 2001 until 2006, when he was succeeded by Sir...
.
Theory
Consider two distinct haploid organisms who differ at a single nucleotideNucleotide
Nucleotides are molecules that, when joined together, make up the structural units of RNA and DNA. In addition, nucleotides participate in cellular signaling , and are incorporated into important cofactors of enzymatic reactions...
. By tracing the ancestry of these two individuals backwards there will be a point in time when the MRCA is encountered and the two lineages will have coalesced.
Time to coalescence
A useful analysis based on coalescence theory seeks to predict the amount of time elapsed between the introduction of a mutation and the arising of a particular allele or gene distribution in a population. This time period is equal to how long ago the most recent common ancestor existed.The probability that two lineage
Lineage (evolution)
An evolutionary lineage is a sequence of species, that form a line of descent, each new species the direct result of speciation from an immediate ancestral species. Lineages are subsets of the evolutionary tree of life. Lineages are often determined by the techniques of molecular systematics.-...
s coalesce in the immediately preceding generation is the probability that they share a parent. In a diploid population with a constant effective population size
Effective population size
In population genetics, the concept of effective population size Ne was introduced by the American geneticist Sewall Wright, who wrote two landmark papers on it...
with 2Ne copies of each locus, there are 2Ne "potential parents" in the previous generation, so the probability that two alleles share a parent is 1/(2Ne) and correspondingly, the probability that they do not coalesce is 1 − 1/(2Ne).
At each successive preceding generation, the probability of coalescence is geometrically distributed — that is, it is the probability of noncoalescence at the t − 1 preceding generations multiplied by the probability of coalescence at the generation of interest:
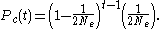
For sufficiently large values of Ne, this distribution is well approximated by the continuously defined exponential distribution
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
The standard exponential distribution has both the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
and the standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
equal to 2Ne; therefore, although the expected time to coalescence is 2Ne, actual coalescence times have a wide range of variation. Note that coalescent time is the number of preceding generations where the coalescence took place and not calendar time though an estimation of the latter can be made multiplying 2Ne with the average time between generations.
Neutral variation
Coalescent theory can also be used to model the amount of variation in DNADNA
Deoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
sequences expected from genetic drift alone. This value is termed the mean heterozygosity, represented as
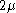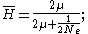
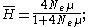
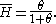
. Mean heterozygosity is calculated as the probability of a mutation occurring at a given generation divided by the probability of any "event" at that generation (either a mutation or a coalescence). The probability that the event is a mutation is the probability of a mutation in either of the two lineages: . Thus the mean heterozygosity is equal toFor
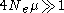, the vast majority of allele pairs have at least one difference in nucleotideNucleotide
Nucleotides are molecules that, when joined together, make up the structural units of RNA and DNA. In addition, nucleotides participate in cellular signaling , and are incorporated into important cofactors of enzymatic reactions...
sequence.
Graphical representation
Coalescents can be visualised using dendrogramDendrogram
A dendrogram is a tree diagram frequently used to illustrate the arrangement of the clusters produced by hierarchical clustering...
s which show the relationship of branches of the population to each other. The point where two branches meet indicates a coalescent event.
Disease gene mapping
The utility of coalescent theory in the mapping of disease is slowly gaining more appreciation; although the application of the theory is still in its infancy, there are a number of researchers who are actively developing algorithms for the analysis of human genetic data that utilise coalescent theory.History
Coalescent theory is a natural extension of the more classical population geneticsPopulation genetics
Population genetics is the study of allele frequency distribution and change under the influence of the four main evolutionary processes: natural selection, genetic drift, mutation and gene flow. It also takes into account the factors of recombination, population subdivision and population...
concept of neutral evolution and is an approximation to the Fisher-Wright (or Wright-Fisher) model for large populations. It was ‘discovered’ independently by several researchers in the 1980’s , but the definitive formalisation is attributed to Kingman . Major contributions to the development of coalescent theory have been made by Peter Donnelly
Peter Donnelly
Peter Donnelly, FRS is an Australian mathematician and Professor of Statistical Science at the University of Oxford. He is a specialist in applied probability and has made contributions to coalescent theory...
, Robert Griffiths
Robert Griffiths (mathematician)
Robert Charles Griffiths, FRS is an Australian mathematician and statistician known for his work in mathematical population genetics. He is Professor of Mathematical Genetics in the University of Oxford and a fellow and tutor at Lady Margaret Hall....
, Richard R Hudson and Simon Tavaré. This has included incorporating variations in population size, recombination and selection. In 1999 Jim Pitman and Serik Sagitov independently introduced coalescent processes with multiple collisions of ancestral lineages. Shortly later the full class of exchangeable coalescent processes with simultaneous multiple mergers of ancestral lineages was discovered by Martin Möhle and Serik Sagitov and Jason Schweinsberg.
Software
A large body of software exists for both simulating data sets under the coalescent process as well as inferring parameters such as population size and migration rates from genetic data.- TreesimJ Forward simulation software allowing sampling of genealogies and data sets under diverse selective and demographic models.
- BEAST - BayesianBayesian inferenceIn statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
MCMCMarkov chain Monte CarloMarkov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
inference package with a wide range of coalescent models including the use of temporally sampled sequences. - CoaSim - software for simulating genetic data under the coalescent model.
- GeneRecon - software for the fine-scale mapping of linkage disequilibriumLinkage disequilibriumIn population genetics, linkage disequilibrium is the non-random association of alleles at two or more loci, not necessarily on the same chromosome. It is also referred to as to as gametic phase disequilibrium , or simply gametic disequilibrium...
mapping of disease genes using coalescent theory based on an BayesianBayesian inferenceIn statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
MCMCMarkov chain Monte CarloMarkov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
framework. - genetree software for estimation of population geneticsPopulation geneticsPopulation genetics is the study of allele frequency distribution and change under the influence of the four main evolutionary processes: natural selection, genetic drift, mutation and gene flow. It also takes into account the factors of recombination, population subdivision and population...
parameters using coalescent theory and simulation (the RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
package popgen). See also Oxford Mathematical Genetics and Bioinformatics Group - GENOME - rapid coalescent-based whole-genome simulation
- Migrate - Maximum likelihoodMaximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
and Bayesian inferenceBayesian inferenceIn statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
of migration rates under the n-coalescent. The inference is implemented using MCMCMarkov chain Monte CarloMarkov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the... - Migraine - A program which implements coalescent algorithms for a maximum likelihood analysis (using Importance SamplingImportance samplingIn statistics, importance sampling is a general technique for estimating properties of a particular distribution, while only having samples generated from a different distribution rather than the distribution of interest. It is related to Umbrella sampling in computational physics...
algortihms) of genetic data with a focus on spatially structured populations . - Lamarc - software for estimation of rates of population growth, migration, and recombination.
- MS & MShot - Richard Hudson's original program for generating samples under neutral models and an extension which allows recombination hotspots.
- SARG - Structure Ancestral Recombination Graph by Magnus Nordborg
- simcoal2 -software to simulate genetic data under the coalescent model with complex demography and recombination
- Recodon and NetRecodon -software to simulate coding sequences with inter/intracodon recombination, migration, growth rate and longitudinal sampling .
- COAL - Program for computing gene tree probabilities and simulating gene trees in species trees under the coalescent model .
- IBDSim - A computer package for the simulation of genotypic data under general isolation by distance models .
Articles
Arenas, M. and Posada, D. (2007) Recodon: Coalescent simulation of coding DNA sequences with recombination, migration and demography. BMC Bioinformatics 8: 458Arenas, M. and Posada, D. (2010) Coalescent simulation of intracodon recombination. Genetics 184(2): 429–437Browning, S.R. (2006) Multilocus association mapping using variable-length markov chains. American Journal of Human Genetics 78:903–913 Degnan, JH and LA Salter. 2005. Gene tree distribtutions under the coalescent process. Evolution 59(1): 24-37. pdf from coaltree.net/Donnelly, P., Tavaré, S. (1995) Coalescents and genealogical structure under neutrality. Annual Review of Genetics 29:401–421Hellenthal, G., Stephens M. (2006) msHOT: modifying Hudson's ms simulator to incorporate crossover and gene conversion hotspots Bioinformatics AOPHudson RR (1983a) Testing the constant-rate neutral allele model with protein sequence data. Evolution 37: 203–207 JSTOR copyHudson RR (1983b) Properties of a neutral allele model with intragenic recombination. Theoretical Population Biology 23:183–201.Hudson RR (1991) Gene genealogies and the coalescent process. Oxford Surveys in Evolutionary Biology 7: 1–44Hudson RR (2002) Generating samples under a Wright–Fisher neutral model. Bioinformatics 18:337–338- Hein, J. , Schierup, M., Wiuf C. (2004) Gene Genealogies, Variation and Evolution: A Primer in Coalescent Theory Oxford University Press ISBN 978-0198529965Kaplan, N.L., Darden, T., Hudson, R.R. (1988) The coalescent process in models with selection. Genetics 120:819–829Kingman, J.F.C. (1982) On the Genealogy of Large Populations. Journal of Applied Probability 19A:27–43 JSTOR copyKingman, J.F.C. (2000) Origins of the coalescent 1974–1982. Genetics 156:1461–1463Liang L., Zöllner S., Abecasis G.R. (2007) GENOME: a rapid coalescent-based whole genome simulator. Bioinformatics 23: 1565–1567Mailund, T., Schierup, M.H., Pedersen, C.N.S., Mechlenborg, P.J.M., Madsen, J.N., Schauser, L. (2005) CoaSim: A Flexible Environment for Simulating Genetic Data under Coalescent Models BMC Bioinformatics 6:252Möhle, M., Sagitov, S. (2001) A classification of coalescent processes for haploid exchangeable population models The Annals of Probability 29:1547–1562Morris, A. P., Whittaker, J. C., Balding, D. J. (2002) Fine-scale mapping of disease loci via shattered coalescent modeling of genealogies American Journal of Human Genetics 70:686–707Neuhauser, C., Krone, S.M. (1997) The genealogy of samples in models with selection Genetics 145 519–534Pitman, J. (1999) Coalescents with multiple collisions The Annals of Probability 27:1870–1902Harding, Rosalind, M. 1998. New phylogenies: an introductory look at the coalescent. Pp. 15-22, in Harvey, P. H., Brown, A. J. L., Smith, J. M., Nee, S. New uses for new phylogenies. Oxford University Press (ISBN:0198549849)Rosenberg, N.A., Nordborg, M. (2002) Genealogical Trees, Coalescent Theory and the Analysis of Genetic Polymorphisms. Nature Reviews Genetics 3:380–390Sagitov, S. (1999) The general coalescent with asynchronous mergers of ancestral lines Journal of Applied Probability 36:1116–1125Schweinsberg, J. (2000) Coalescents with simultaneous multiple collisions Electronic Journal of Probability 5:1–50Slatkin, M. (2001) Simulating genealogies of selected alleles in populations of variable size Genetic Research 145:519–534Tajima, F. (1983) Evolutionary Relationship of DNA Sequences in finite populations. Genetics 105:437–460Zöllner S. and Pritchard J.K.Jonathan K. PritchardJonathan K. Pritchard is an English-born professor of genetics at the University of Chicago. His research interests lie in the study of human evolution, in particular in understanding the association between genetic variation among human individuals and human traits.Pritchard's family moved to the...
(2005) Coalescent-Based Association Mapping and Fine Mapping of Complex Trait Loci Genetics 169:1071–1092Rousset F. and Leblois R. (2007) Likelihood and Approximate Likelihood Analyses of Genetic Structure in a Linear Habitat: Performance and Robustness to Model Mis-Specification Molecular Biology and Evolution 24:2730–2745Leblois R., Estoup A. and Rousset F. (2009) IBDSim: a computer program to simulate genotypic data under isolation by distance Molecular Ecology Resources 9:107-109
Books
- Hein, J; Schierup, M. H., and Wiuf, C. Gene Genealogies, Variation and Evolution – A Primer in Coalescent Theory. Oxford University PressOxford University PressOxford University Press is the largest university press in the world. It is a department of the University of Oxford and is governed by a group of 15 academics appointed by the Vice-Chancellor known as the Delegates of the Press. They are headed by the Secretary to the Delegates, who serves as...
, 2005. ISBN 0-19-852996-1. - Nordborg, M. (2001) Introduction to Coalescent Theory
- Chapter 7 in Balding, D., Bishop, M., Cannings, C., editors, Handbook of Statistical Genetics. Wiley ISBN 978-0471860945
- Wakeley J. (2006) An Introduction to Coalescent Theory Roberts & Co ISBN 0-9747077-5-9 Accompanying website with sample chapters Rice SH. (2004). Evolutionary Theory: Mathematical and Conceptual Foundations. Sinauer Associates: Sunderland, MA. See esp. ch. 3 for detailed derivations.
- Berestycki N. "Recent progress in coalescent theory" 2009 ENSAIOS Matematicos vol.16
- Bertoin J. "Random Fragmentation and Coagulation Processes"., 2006. Cambridge Studies in Advanced Mathematics, 102. Cambridge University PressCambridge University PressCambridge University Press is the publishing business of the University of Cambridge. Granted letters patent by Henry VIII in 1534, it is the world's oldest publishing house, and the second largest university press in the world...
, Cambridge, 2006. ISBN 978-0-521-86728-3; - Pitman J. "Combinatorial stochastic processes" Springer (2003)
External links
- EvoMath 3: Genetic Drift and Coalescence, Briefly — overview, with probability equations for genetic drift, and simulation graphs