Werner state
Encyclopedia
A Werner state is a -dimensional bipartite quantum state that is invariant
under all unitary operators
of the form
. That is, it is a quantum state ρ that satisfies
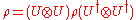
for all unitary operators U acting on d-dimensional Hilbert space.
Every Werner state is a mixture of projector
s onto the symmetric
and antisymmetric subspace
s, with the relative weight psym being the only parameter that defines the state.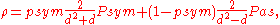
where
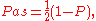
are the projectors and
is the permutation operator that exchanges the two subsystems.
Werner states are separable
for psym ≥ and entangled for psym < . All entangled Werner states violate the PPT separability criterion
, but for d ≥ 3 no Werner states violate the weaker reduction criterion
. Werner states can be parametrized in different ways. One way of writing them is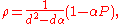
where the new parameter α varies between −1 and 1 and relates to psym as
for any unitary U on a single subsystem. The Werner state is no longer described by a single parameter, but by N! − 1 parameters, and is a linear combination of the N! different permutations on N systems.
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
under all unitary operators
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
of the form
. That is, it is a quantum state ρ that satisfies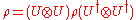for all unitary operators U acting on d-dimensional Hilbert space.
Every Werner state is a mixture of projector
Projector
Projector may refer to:*Image projector, a device that projects an image on a surface** Video projector, a device that projects a video signal from computer, home theater system etc.** Movie projector, a device that projects moving pictures from a filmstrip...
s onto the symmetric
Symmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
and antisymmetric subspace
Subspace
-In mathematics:* Euclidean subspace, in linear algebra, a set of vectors in n-dimensional Euclidean space that is closed under addition and scalar multiplication...
s, with the relative weight psym being the only parameter that defines the state.
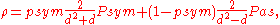
where
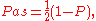
are the projectors and
is the permutation operator that exchanges the two subsystems.
Werner states are separable
Separable states
In quantum mechanics, separable quantum states are states without quantum entanglement.- Separable pure states :For simplicity, the following assumes all relevant state spaces are finite dimensional...
for psym ≥ and entangled for psym < . All entangled Werner states violate the PPT separability criterion
Peres-Horodecki criterion
The Peres-Horodecki criterion is a necessary condition, for the joint density matrix \rho of two quantum mechanical systems A and B, to be separable. It is also called the PPT criterion, for positive partial transpose. In the 2x2 and 2x3 dimensional cases the condition is also sufficient...
, but for d ≥ 3 no Werner states violate the weaker reduction criterion
Reduction criterion
In quantum information theory, the reduction criterion is a necessary condition a mixed state must satisfy in order for it to be separable. In other words, the reduction criterion is a separability criterion.-Details:...
. Werner states can be parametrized in different ways. One way of writing them is
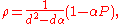
where the new parameter α varies between −1 and 1 and relates to psym as
Multipartite Werner states
Werner states can be generalized to the multipartite case . An N-party Werner state is a state that is invariant under for any unitary U on a single subsystem. The Werner state is no longer described by a single parameter, but by N! − 1 parameters, and is a linear combination of the N! different permutations on N systems.