Separable states
Encyclopedia
In quantum mechanics
, separable quantum states are states without quantum entanglement
.
Let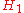
and 
be quantum mechanical state spaces, that is, finite dimensional Hilbert space
s with basis states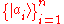
and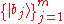 
, respectively. By a postulate of quantum mechanics, the state space of the composite system is given by the tensor product
with base states
, or in more compact notation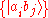 
. From the very definition of the tensor product, any vector of norm 1, i.e. a pure state of the composite system, can be written as
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, separable quantum states are states without quantum entanglement
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
.
Separable pure states
For simplicity, the following assumes all relevant state spaces are finite dimensional. First, consider separability for pure states.Let
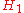and be quantum mechanical state spaces, that is, finite dimensional Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s with basis states
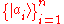and 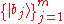, respectively. By a postulate of quantum mechanics, the state space of the composite system is given by the tensor productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
with base states
, or in more compact notation 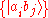. From the very definition of the tensor product, any vector of norm 1, i.e. a pure state of the composite system, can be written as-
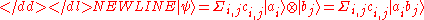
If a pure state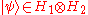
can be written in the form 
where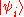 
is a pure state of the i-th subsystem, it is said to be separable. Otherwise it is called entangled. Formally, the embedding of a product of states into the product space is given by the Segre embeddingSegre embeddingIn mathematics, the Segre embedding is used in projective geometry to consider the cartesian product of two or more projective spaces as a projective variety...
. That is, a quantum-mechanical pure state is separable if and only if it is in the image of the Segre embedding.
A standard example of an (un-normalized) entangled state is
where H is the Hilbert space of dimension 2. We see that when a system is in an entangled pure state, it is not possible to assign states to its subsystems. This will be true, in the appropriate sense, for the mixed state case as well.
The above discussion can be extended to the case of when the state space is infinite dimensional with virtually nothing changed.
Separability for mixed states
Consider the mixed state case. A mixed state of the composite system is described by a density matrixDensity matrixIn quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
acting on 
. ρ is separable if there exist 
, 
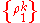and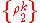 
which are mixed states of the respective subsystems such that
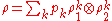
where
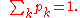
Otherwise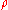
is called an entangled state. We can assume without loss of generality in the above expression that 
and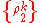 
are all rank-1 projections, that is, they represent pure ensembles of the appropriate subsystems. It is clear from the definition that the family of separable states is a convex setConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
.
Notice that, again from the definition of the tensor product, any density matrix, indeed any matrix acting on the composite state space, can be trivially written in the desired form, if we drop the requirement that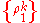
and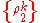 
are themselves states and 
If these requirements are satisfied, then we can interpret the total state as a probability distribution over uncorrelated product stateProduct stateIn quantum mechanics, a product state, or simply separable state, is a special type of separable state in which there are neither classical nor quantum correlations. Precisely, it is a joint state of two systems which can be expressed as...
s.
In terms of quantum channelQuantum channelIn quantum information theory, a quantum channel is a communication channel which can transmit quantum information, as well as classical information. An example of quantum information is the state of a qubit...
s, a separable state can be created from any other state using local actions and classical communicationLOCCLOCC, or Local Operations and Classical Communication, is a method in quantum information theory where a local operation is performed on part of the system, and where the result of that operation is "communicated" classically to another part where usually another local operation is performed...
while an entangled state cannot.
When the state spaces are infinite dimensional, density matrices are replaced by positive trace classTrace classIn mathematics, a trace class operator is a compact operator for which a trace may be defined, such that the trace is finite and independent of the choice of basis....
operators with trace 1, and a state is separable if it can be approximated, in trace norm, by states of the above form.
If there is only a single non-zero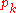
, then the state is called simply separable (or it is called a "product state").
Extending to the multipartite case
The above discussion generalizes easily to the case of a quantum system consisting of more than two subsystems. Let a system have n subsystems and have state space
. A pure state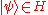 
is separable if it takes the form
Similarly, a mixed state ρ acting on H is separable if it is a convex sum
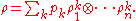
Or, in the infinite dimensional case, ρ is separable if it can be approximated in the trace norm by states of the above form.
Separability criterion
The problem of deciding whether a state is separable in general is sometimes called the separability problem in quantum information theory. It is considered to be a difficult problem. It has been shown to be NP-hardNP-hardNP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
. Some appreciation for this difficulty can be obtained if one attempts to solve the problem by employing the direct brute force approach, for a fixed dimension. We see that the problem quickly becomes intractable, even for low dimensions. Thus more sophisticated formulations are required. The separability problem is a subject of current research.
A separability criterion is a necessary condition a state must satisfy to be separable. In the low dimensional (2 X 2 and 2 X 3) cases, the Peres-Horodecki criterionPeres-Horodecki criterionThe Peres-Horodecki criterion is a necessary condition, for the joint density matrix \rho of two quantum mechanical systems A and B, to be separable. It is also called the PPT criterion, for positive partial transpose. In the 2x2 and 2x3 dimensional cases the condition is also sufficient...
is actually a necessary and sufficient condition for separability. Other separability criteria include the range criterionRange criterionIn quantum mechanics, in particular quantum information, the Range criterion is a necessary condition that a state must satisfy in order to be separable. In other words, it is a separability criterion.- The result :...
and reduction criterionReduction criterionIn quantum information theory, the reduction criterion is a necessary condition a mixed state must satisfy in order for it to be separable. In other words, the reduction criterion is a separability criterion.-Details:...
.
Characterization via algebraic geometry
Quantum mechanics may be modelled on a projective Hilbert spaceProjective Hilbert spaceIn mathematics and the foundations of quantum mechanics, the projective Hilbert space P of a complex Hilbert space H is the set of equivalence classes of vectors v in H, with v ≠ 0, for the relation given by...
, and the categorical product of two such spaces is the Segre embeddingSegre embeddingIn mathematics, the Segre embedding is used in projective geometry to consider the cartesian product of two or more projective spaces as a projective variety...
. In the bipartite case, a quantum state is separable if and only if it lies in the imageImage (mathematics)In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of the Segre embedding.