Quantum channel
Encyclopedia
In quantum information theory, a quantum channel is a communication channel which can transmit quantum information
, as well as classical information. An example of quantum information is the state of a qubit
. An example of classical information is a text document transmitted over the internet
.
More formally, quantum channels are completely positive, trace preserving maps between spaces of operators. In other words, a quantum channel is just a quantum operation
viewed not merely as the reduced dynamics of a system but as a pipeline intended to carry quantum information.
The memory-less in the section title carries the same meaning as in classical information theory
: the output of a channel at a given time depends only upon the corresponding input and not any previous ones.
, whose properties we now summarize.
Let
and 
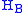be the state spaces (finite-dimensional Hilbert space
s) of the sending and receiving ends, respectively, of a channel.
will denote the family of operators on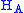 
. In the Schrödinger picture
, a purely quantum channel is a map Φ between density matrices
acting on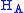
and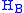 
with the following properties:
The adjectives completely positive and trace preserving used to described a map are sometimes abbreviated CPTP. We note here that, in the literature, sometimes the fourth property is weakened so that Φ is only required to be not trace-increasing. In this article, it will be assumed that all channels are CPTP.
:
The spaces of operators L(HA) and L(HB) are Hilbert spaces with the Hilbert-Schmidt inner product. Therefore, viewing
as a map between Hilbert spaces, we obtain its adjoint Φ* given by
While Φ takes states on A to those on B, Φ* maps observables on system B to observables on A. This relationship is same as that between the Schrödinger and Heisenberg descriptions of dynamics. The measurement statistics remain unchanged whether the observables are considered fixed while the states undergo operation or vice versa.
It can be directly checked that if Φ is assumed to be trace preserving, Φ* is unital
, that is,Φ*(I) = I. Physically speaking, this means that, in the Heisenberg picture, the trivial observable remains trivial after applying the channel.
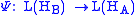
that is unital and completely positive (CP). The operator spaces can be viewed as finite dimensional
C*-algebras. Therefore we can say a channel is a unital CP map between C*-algebras:
Classical information can then be included in this formulation. The observables of a classical system can be
assumed to be a commutative C*-algebra, i.e. the space of continuous functions C(X) on some set X. We assume X is finite so C(X) can be identified with the n-dimensional Euclidean space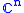
with entry-wise multiplication.
Therefore, in the Heisenberg picture, if the classical information is part of, say, the input, we would define
to include the relevant classical observables. An example of this would be a channel
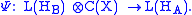
Notice
is still a C*-algebra. A element a of a C*-algebra 
is called positive if a = x*x for some x. Positivity of a map is defined accordingly.
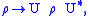
where
and H is the Hamiltonian
at time t. Clearly this gives a CPTP map in the Schrödinger picture and is therefore a channel. The dual map in the Heisenberg picture is
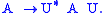
For a state
the reduced state of ρ on system A, ρA, is obtained by taking the partial trace
of ρ with respect to the B system:
The partial trace operation is a CPTP map, therefore a quantum channel in the Schrödinger picture. In the Heisenberg picture, the dual map of this channel is
where A is an observable of system A.
to a quantum mechanical effect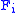 
. 
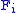's are assumed to be positive operators acting on appropriate state space and 
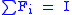. (Such a collection is called a POVM
.) In the Heisenberg picture, the corresponding observable map Ψ maps a classical observable
to the quantum mechanical one
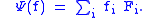
In other words, one integrate f against the POVM
to obtain the quantum mechanical observable. It can be easily checked that Ψ is CP and unital.
The corresponding Schrödinger map Ψ* takes density matrices to classical states:
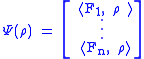
,where the inner product is the Hilbert-Schmidt inner product. Furthermore, viewing states as normalized functionals, and invoking the Riesz representation theorem
, we can put
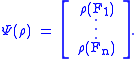
be the effects (POVM) associated to an observable. In the Schrödinger picture, an instrument is a map Φ with pure quantum input 
and with output space 
:
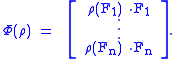
Let
The dual map in the Heisenberg picture is
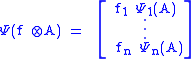
where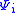
is defined in the following way: Factor 
(this can always be done since elements of a POVM are positive) then 
.
We see that Ψ is CP and unital.
Notice that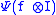
gives precisely the observable map. The map
describes the overall state change.
. Suppose two parties A and B wish to communicate in the following manner: A performs measurement on an observable and communicates the measurement outcome to B classically. According to the message he receives, B prepares his (quantum) system in a state that is previously agreed upon by both parties. In the Schrödinger picture, the first part of the channel Φ1 simply consists of A making a measurement, i.e. it is the observable map:
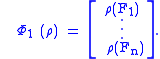
If, in the event of the i-th measurement outcome, B prepares his system in state Ri, the second part of the channel Φ2 takes the above classical state to the density matrix
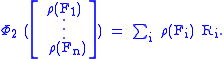
The total operation is the composition
Channels of this form are called separable or in Holevo form
.
In the Heisenberg picture, the dual map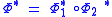
is defined by
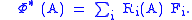
A separable channel can not be the identity map. This is precisely the statement of the no teleportation theorem
, which says classical teleportation (not to be confused with entanglement-assisted teleportation
) is impossible. In other words, a quantum state can not be measured reliably.
In the channel-state duality
, a channel is separable if and only if the corresponding state is separable. Several other characterizations of separable channels are known, notably that a channel is separable if and only if it is entanglement-breaking.
By Choi's theorem on completely positive maps
, Ψ must take the form
where N ≤ nm. The matrices Ki are called Kraus operators of Ψ. The minimum number of Kraus operators is call the Kraus rank of Ψ. A channel with Kraus rank 1 is called pure. The time evolution is one example of a pure channel. This terminology again comes from the channel-state duality. A channel is pure if and only if its dual state is a pure state. Since this duality preserves the extremal points, the extremal points in the convex set of channels are precisely the pure channels.
, a sender wishes to transmit an arbitrary quantum state of a particle to a possibly distant receiver. Consequently, the teleportation process is a quantum channel. The apparatus for the process itself requires a quantum channel for the transmission of one particle of an entangled-state to the receiver. Teleportation occurs by a joint measurement of the send particle and the remaining entangled particle. This measurement results in classical information which must be sent to the receiver to complete the teleportation. Importantly, the classical information can be sent after the quantum channel has ceased to exist. The send particle is destroyed in the measurement and thus is not actually moved from one location to another to create the quantum channel.
s. Single photons can be transmitted up to 100 km in standard fiber optics before losses dominate. The photon's time-of-arrival (time-bin entanglement) or polarization are used as a basis to encode quantum information for purposes such as quantum cryptography
. The channel is capable of transmitting not only basis states (e.g. |0>, |1>) but also superpositions of them (e.g. |0>+|1>). The coherence of the state is maintained during transmission through the channel. Contrast this with the transmission of electrical pulses through wires (a classical channel), where only classical information (e.g. 0s and 1s) can be sent.
between channels.
Since a channel can be viewed as a linear operator, it is tempting to use the natural operator norm
. In other words, the closenss of Φ to the ideal channel Λ can be defined by
However, the operator norm may increase when we tensor Φ with the identity map on some ancilla.
To make the operator norm even a more undesirable candidate, the quantity
may increase without bound as
The solution is to introduce, for any linear map Φ between C*-algebras, the cb-norm
.
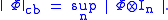
Let
be a channel in the Heisenberg picture and 
be a chosen ideal channel. To make the comparison possible, one needs to encode and decode Φ via appropriate devices, i.e. we consider the composition
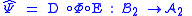
where E is an encoder
and D is a decoder
. In this context, E and D are unital CP maps with appropriate domains. The quantity of interest is the best case scenario:
with the infimum being taken over all possible encoders and decoders.
To transmit words of length n, the ideal channel is to be applied n times, so we consider the tensor power
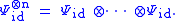
The
operation describes n inputs undergoing the operation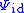 
independently and is the quantum mechanical counterpart of concatenation
. Similarly, m-invokations of the channel corresponds to
.
The quantity
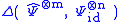
is therefore a measure of the ability of the channel to transmit words of length n faithfully by being invoked m times.
This leads to the following definition:
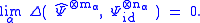
A sequence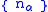
can be viewed as representing a message consisting of possibly infinite number of words. The limit supremum condition in the definition says that, in the limit, faithful transmission can be achieved by invoking the channel no more than r times the length of a word. One can also say that r is the number of letters per invokation of the channel that can be sent without error.
The channel capacity of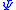
with respect to 
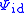, denoted by 
is the supremum of all achievable rates.
From the definition, it is vacuously true that 0 is an achievable rate for any channel.
, the ideal channel 
is by definition the identity map 
. Thus for a purely n dimensional quantum system, the ideal channel is the identity map on the space of n x n matrices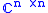 
. As a slight abuse of notation, this ideal quantum channel will be also denoted by 
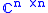. Similarly for a classical system with output algebra 
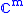will have an ideal channel denoted by the same symbol. We can now state some fundamental channel capacities.
The channel capacity of the classical ideal channel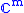
with respect to a quantum ideal channel 
is
This is equivalent to the no-teleportation theorem: it is impossible to transmit quantum information via a classical channel.
Moreover, the following equalities hold:
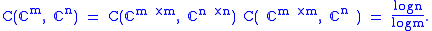
The above says, for instance, an ideal quantum channel is no more efficient at transmitting classical information than an ideal classical channel. When n = m, the best one can achieve is one bit per qubit.
Remark It is relevant to note here that both of the above bounds on capacities can be broken, with the aid of entanglement
. The entanglement-assisted teleportation scheme
allows one to transmit quantum information using a classical channel. Superdense coding
. achieves two bit per qubit. These results indicate the significant role played by entanglement in quantum communication.
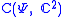
, that is, it is the capacity of Ψ with respect to the ideal channel on the classical one-bit system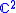
.
Similarly the quantum capacity of Ψ is
, where the reference system is now the one qubit system
.
.
Quantum information
In quantum mechanics, quantum information is physical information that is held in the "state" of a quantum system. The most popular unit of quantum information is the qubit, a two-level quantum system...
, as well as classical information. An example of quantum information is the state of a qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
. An example of classical information is a text document transmitted over the internet
Internet
The Internet is a global system of interconnected computer networks that use the standard Internet protocol suite to serve billions of users worldwide...
.
More formally, quantum channels are completely positive, trace preserving maps between spaces of operators. In other words, a quantum channel is just a quantum operation
Quantum operation
In quantum mechanics, a quantum operation is a mathematical formalism used to describe a broad class of transformations that a quantum mechanical system can undergo. This was first discussed as a general stochastic transformation for a density matrix by George Sudarshan...
viewed not merely as the reduced dynamics of a system but as a pipeline intended to carry quantum information.
Memoryless quantum channel
We will assume for the moment that all state spaces of the systems considered, classical or quantum, are finite dimensional.The memory-less in the section title carries the same meaning as in classical information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
: the output of a channel at a given time depends only upon the corresponding input and not any previous ones.
Schrödinger picture
Consider quantum channels that transmit only quantum information. This is precisely a quantum operationQuantum operation
In quantum mechanics, a quantum operation is a mathematical formalism used to describe a broad class of transformations that a quantum mechanical system can undergo. This was first discussed as a general stochastic transformation for a density matrix by George Sudarshan...
, whose properties we now summarize.
Let
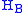and be the state spaces (finite-dimensional Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s) of the sending and receiving ends, respectively, of a channel.
will denote the family of operators on 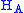. In the Schrödinger pictureSchrödinger picture
In physics, the Schrödinger picture is a formulation of quantum mechanics in which the state vectors evolve in time, but the operators are constant. This differs from the Heisenberg picture which keeps the states constant while the observables evolve in time...
, a purely quantum channel is a map Φ between density matrices
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
acting on
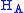and 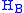with the following properties:- As required by postulates of quantum mechanics, Φ needs to be linear.
- Since density matrices are positive, Φ must preserve the coneCone (linear algebra)In linear algebra, a cone is a subset of a vector space that is closed under multiplication by positive scalars. In other words, a subset C of a real vector space V is a cone if and only if λx belongs to C for any x in C and any positive scalar λ of V .A cone is said...
of positive elements. In other words, Φ is a positive mapChoi's theorem on completely positive mapsIn mathematics, Choi's theorem on completely positive maps is a result that classifies completely positive maps between finite-dimensional C*-algebras...
. - If we couple an ancilla of arbitrary finite dimension n to the system, and the induced map
, where In is the identity map on the ancilla, must also be positive. Therefore it is required that 
is positive for all n. We call such maps completely positive. - Density matrices are specified to have trace 1, so Φ has to preserve the trace.
The adjectives completely positive and trace preserving used to described a map are sometimes abbreviated CPTP. We note here that, in the literature, sometimes the fourth property is weakened so that Φ is only required to be not trace-increasing. In this article, it will be assumed that all channels are CPTP.
Heisenberg picture
Density matrices acting on HA only constitute a proper subset of the operators on HA and same can be said for system B. However, once a linear map Φ between the density matrices is specified, a standard linearity argument, together with the finite dimensional assumption, allow us to extend Φ uniquely to the full space of operators. This leads to the adjoint map Φ*, which describes the action of Φ in the Heisenberg pictureHeisenberg picture
In physics, the Heisenberg picture is a formulation of quantum mechanics in which the operators incorporate a dependency on time, but the state vectors are time-independent. It stands in contrast to the Schrödinger picture in which the operators are constant and the states evolve in time...
:
The spaces of operators L(HA) and L(HB) are Hilbert spaces with the Hilbert-Schmidt inner product. Therefore, viewing
as a map between Hilbert spaces, we obtain its adjoint Φ* given byWhile Φ takes states on A to those on B, Φ* maps observables on system B to observables on A. This relationship is same as that between the Schrödinger and Heisenberg descriptions of dynamics. The measurement statistics remain unchanged whether the observables are considered fixed while the states undergo operation or vice versa.
It can be directly checked that if Φ is assumed to be trace preserving, Φ* is unital
Unital map
In abstract algebra, a unital map on a C*-algebra is a map \phi which preserves the identity element:\phi = I. \, This condition appears often in the context of completely positive maps, especially when they represent quantum operations....
, that is,Φ*(I) = I. Physically speaking, this means that, in the Heisenberg picture, the trivial observable remains trivial after applying the channel.
Classical information
So far we have only defined quantum channel that transmits only quantum information. As stated in the introduction, the input and output of a channel can include classical information as well. To describe this, the formulation given so far needs to be generalized somewhat. A purely quantum channel, in the Heisenberg picture, is a linear map Ψ between spaces of operators: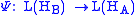that is unital and completely positive (CP). The operator spaces can be viewed as finite dimensional
C*-algebras. Therefore we can say a channel is a unital CP map between C*-algebras:
Classical information can then be included in this formulation. The observables of a classical system can be
assumed to be a commutative C*-algebra, i.e. the space of continuous functions C(X) on some set X. We assume X is finite so C(X) can be identified with the n-dimensional Euclidean space
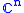with entry-wise multiplication.Therefore, in the Heisenberg picture, if the classical information is part of, say, the input, we would define
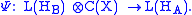
to include the relevant classical observables. An example of this would be a channelNotice
is still a C*-algebra. A element a of a C*-algebra is called positive if a = x*x for some x. Positivity of a map is defined accordingly.States
A state, viewed as a mapping from observables to their expectation values, is an immediate example of a channel.Time evolution
For a purely quantum system, the time evolution, up to certain time t, is given by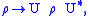where
and H is the HamiltonianHamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
at time t. Clearly this gives a CPTP map in the Schrödinger picture and is therefore a channel. The dual map in the Heisenberg picture is
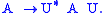
Restriction
Consider a composite quantum system with state space For a statethe reduced state of ρ on system A, ρA, is obtained by taking the partial trace
Partial trace
In linear algebra and functional analysis, the partial trace is a generalization of the trace. Whereas the trace is a scalar valued function on operators, the partial trace is an operator-valued function...
of ρ with respect to the B system:
The partial trace operation is a CPTP map, therefore a quantum channel in the Schrödinger picture. In the Heisenberg picture, the dual map of this channel is
where A is an observable of system A.
Observable
An observable associates a numerical value to a quantum mechanical effect 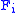. 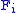's are assumed to be positive operators acting on appropriate state space and 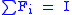. (Such a collection is called a POVMPOVM
In functional analysis and quantum measurement theory, a POVM is a measure whose values are non-negative self-adjoint operators on a Hilbert space. It is the most general formulation of a measurement in the theory of quantum physics...
.) In the Heisenberg picture, the corresponding observable map Ψ maps a classical observable
to the quantum mechanical one
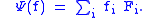
In other words, one integrate f against the POVM
Naimark's dilation theorem
In operator theory, Naimark's dilation theorem is a result that characterizes positive operator valued measures. It can be viewed as a consequence of Stinespring's dilation theorem.- Note :...
to obtain the quantum mechanical observable. It can be easily checked that Ψ is CP and unital.
The corresponding Schrödinger map Ψ* takes density matrices to classical states:
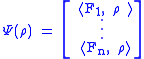
,where the inner product is the Hilbert-Schmidt inner product. Furthermore, viewing states as normalized functionals, and invoking the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
, we can put
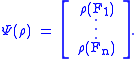
Instrument
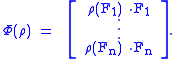
The observable map, in the Schrödinger picture, has a purely classical output algebra and therefore only describe measurement statistics. To take the state change into account as well, we define what is called an instrument. Let be the effects (POVM) associated to an observable. In the Schrödinger picture, an instrument is a map Φ with pure quantum input and with output space :Let
The dual map in the Heisenberg picture is
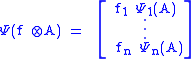
where
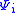is defined in the following way: Factor (this can always be done since elements of a POVM are positive) then .We see that Ψ is CP and unital.
Notice that
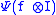gives precisely the observable map. The mapdescribes the overall state change.
Separable channel
A separable channel is an example of local operation and classical communication (LOCC)LOCC
LOCC, or Local Operations and Classical Communication, is a method in quantum information theory where a local operation is performed on part of the system, and where the result of that operation is "communicated" classically to another part where usually another local operation is performed...
. Suppose two parties A and B wish to communicate in the following manner: A performs measurement on an observable and communicates the measurement outcome to B classically. According to the message he receives, B prepares his (quantum) system in a state that is previously agreed upon by both parties. In the Schrödinger picture, the first part of the channel Φ1 simply consists of A making a measurement, i.e. it is the observable map:
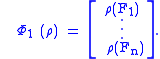
If, in the event of the i-th measurement outcome, B prepares his system in state Ri, the second part of the channel Φ2 takes the above classical state to the density matrix
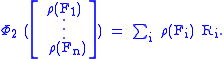
The total operation is the composition
Channels of this form are called separable or in Holevo form
Holevo's theorem
In physics, in the area of quantum information theory, Holevo's theorem is an important limitative theorem in quantum computing which was published by in 1973....
.
In the Heisenberg picture, the dual map
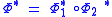is defined by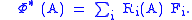A separable channel can not be the identity map. This is precisely the statement of the no teleportation theorem
No teleportation theorem
In quantum information theory, the no-teleportation theorem states that quantum information cannot be measured with complete accuracy.-Formulation:The term quantum information refers to information stored in the state of a quantum system...
, which says classical teleportation (not to be confused with entanglement-assisted teleportation
Quantum teleportation
Quantum teleportation, or entanglement-assisted teleportation, is a process by which a qubit can be transmitted exactly from one location to another, without the qubit being transmitted through the intervening space...
) is impossible. In other words, a quantum state can not be measured reliably.
In the channel-state duality
Channel-state duality
In quantum information theory, the channel-state duality refers to the correspondence between quantum channels and quantum states...
, a channel is separable if and only if the corresponding state is separable. Several other characterizations of separable channels are known, notably that a channel is separable if and only if it is entanglement-breaking.
Pure channel
Consider the case of a purely quantum channel Ψ in the Heisenberg picture. With the assumption that everything is finite dimensional, Ψ is a unital CP map between spaces of matrices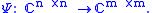By Choi's theorem on completely positive maps
Choi's theorem on completely positive maps
In mathematics, Choi's theorem on completely positive maps is a result that classifies completely positive maps between finite-dimensional C*-algebras...
, Ψ must take the form
where N ≤ nm. The matrices Ki are called Kraus operators of Ψ. The minimum number of Kraus operators is call the Kraus rank of Ψ. A channel with Kraus rank 1 is called pure. The time evolution is one example of a pure channel. This terminology again comes from the channel-state duality. A channel is pure if and only if its dual state is a pure state. Since this duality preserves the extremal points, the extremal points in the convex set of channels are precisely the pure channels.
Teleportation
In quantum teleportationQuantum teleportation
Quantum teleportation, or entanglement-assisted teleportation, is a process by which a qubit can be transmitted exactly from one location to another, without the qubit being transmitted through the intervening space...
, a sender wishes to transmit an arbitrary quantum state of a particle to a possibly distant receiver. Consequently, the teleportation process is a quantum channel. The apparatus for the process itself requires a quantum channel for the transmission of one particle of an entangled-state to the receiver. Teleportation occurs by a joint measurement of the send particle and the remaining entangled particle. This measurement results in classical information which must be sent to the receiver to complete the teleportation. Importantly, the classical information can be sent after the quantum channel has ceased to exist. The send particle is destroyed in the measurement and thus is not actually moved from one location to another to create the quantum channel.
In the experimental setting
Experimentally, a simple implementation of a quantum channel is fiber optic (or free-space for that matter) transmission of single photonPhoton
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s. Single photons can be transmitted up to 100 km in standard fiber optics before losses dominate. The photon's time-of-arrival (time-bin entanglement) or polarization are used as a basis to encode quantum information for purposes such as quantum cryptography
Quantum cryptography
Quantum key distribution uses quantum mechanics to guarantee secure communication. It enables two parties to produce a shared random secret key known only to them, which can then be used to encrypt and decrypt messages...
. The channel is capable of transmitting not only basis states (e.g. |0>, |1>) but also superpositions of them (e.g. |0>+|1>). The coherence of the state is maintained during transmission through the channel. Contrast this with the transmission of electrical pulses through wires (a classical channel), where only classical information (e.g. 0s and 1s) can be sent.
The cb-norm of a channel
Before giving the definition of channel capacity, the preliminary notion of the norm of complete boundedness, or cb-norm of a channel needs to be discussed. When considering the capacity of a channel Φ, we need to compare it with an "ideal channel" Λ. For instance, when the input and output algebras are identical, we can choose Λ to be the identity map. Such a comparison requires a metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
between channels.
Since a channel can be viewed as a linear operator, it is tempting to use the natural operator norm
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
. In other words, the closenss of Φ to the ideal channel Λ can be defined by
However, the operator norm may increase when we tensor Φ with the identity map on some ancilla.
To make the operator norm even a more undesirable candidate, the quantity
may increase without bound as
The solution is to introduce, for any linear map Φ between C*-algebras, the cb-norm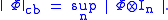Definition of Channel Capacity
We remind the reader that the mathematical model of a channel used here is same as the classical oneChannel capacity
In electrical engineering, computer science and information theory, channel capacity is the tightest upper bound on the amount of information that can be reliably transmitted over a communications channel...
.
Let
be a channel in the Heisenberg picture and be a chosen ideal channel. To make the comparison possible, one needs to encode and decode Φ via appropriate devices, i.e. we consider the composition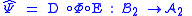where E is an encoder
Encoder
An encoder is a device, circuit, transducer, software program, algorithm or person that converts information from one format or code to another, for the purposes of standardization, speed, secrecy, security, or saving space by shrinking size.-Media:...
and D is a decoder
Decoder
A decoder is a device which does the reverse operation of an encoder, undoing the encoding so that the original information can be retrieved. The same method used to encode is usually just reversed in order to decode...
. In this context, E and D are unital CP maps with appropriate domains. The quantity of interest is the best case scenario:
with the infimum being taken over all possible encoders and decoders.
To transmit words of length n, the ideal channel is to be applied n times, so we consider the tensor power
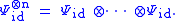
The
operation describes n inputs undergoing the operation 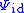independently and is the quantum mechanical counterpart of concatenationConcatenation
In computer programming, string concatenation is the operation of joining two character strings end-to-end. For example, the strings "snow" and "ball" may be concatenated to give "snowball"...
. Similarly, m-invokations of the channel corresponds to
.The quantity
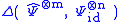
is therefore a measure of the ability of the channel to transmit words of length n faithfully by being invoked m times.
This leads to the following definition:
- An a non-negative real number r is an achievable rate of
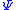with respect to 
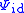if
- For all sequences
where 
and 
, we have
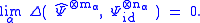
A sequence
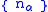can be viewed as representing a message consisting of possibly infinite number of words. The limit supremum condition in the definition says that, in the limit, faithful transmission can be achieved by invoking the channel no more than r times the length of a word. One can also say that r is the number of letters per invokation of the channel that can be sent without error.The channel capacity of
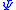with respect to 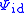, denoted by is the supremum of all achievable rates.From the definition, it is vacuously true that 0 is an achievable rate for any channel.
Important examples
As stated before, for a system with observable algebra, the ideal channel is by definition the identity map . Thus for a purely n dimensional quantum system, the ideal channel is the identity map on the space of n x n matrices 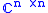. As a slight abuse of notation, this ideal quantum channel will be also denoted by 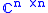. Similarly for a classical system with output algebra 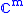will have an ideal channel denoted by the same symbol. We can now state some fundamental channel capacities.The channel capacity of the classical ideal channel
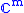with respect to a quantum ideal channel isThis is equivalent to the no-teleportation theorem: it is impossible to transmit quantum information via a classical channel.
Moreover, the following equalities hold:
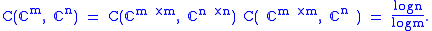
The above says, for instance, an ideal quantum channel is no more efficient at transmitting classical information than an ideal classical channel. When n = m, the best one can achieve is one bit per qubit.
Remark It is relevant to note here that both of the above bounds on capacities can be broken, with the aid of entanglement
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
. The entanglement-assisted teleportation scheme
Quantum teleportation
Quantum teleportation, or entanglement-assisted teleportation, is a process by which a qubit can be transmitted exactly from one location to another, without the qubit being transmitted through the intervening space...
allows one to transmit quantum information using a classical channel. Superdense coding
Superdense coding
Superdense coding is a technique used in quantum information theory to send two bits of classical information using only one qubit, with the aid of entanglement.- Overview :...
. achieves two bit per qubit. These results indicate the significant role played by entanglement in quantum communication.
Classical and quantum channel capacities
Using the same notation as the previous subsection, the classical capacity of a channel Ψ is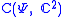, that is, it is the capacity of Ψ with respect to the ideal channel on the classical one-bit system
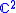.Similarly the quantum capacity of Ψ is
, where the reference system is now the one qubit system
.Channel fidelity
Another measure of how well a quantum channel preserves information is called channel fidelity, and it arises from fidelity of quantum statesFidelity of quantum states
In quantum information theory, fidelity is a measure of the "closeness" of two quantum states. It is not a metric on the space of density matrices, but it can be used to define the Bures metric on this space.- Motivation :...
.