POVM
Encyclopedia
In functional analysis
and quantum measurement theory, a POVM (Positive Operator Valued Measure) is a measure
whose values are non-negative self-adjoint operator
s on a Hilbert space
. It is the most general formulation of a measurement in the theory of quantum physics. The need for the POVM formalism arises from the fact that projective measurements on a larger system will act on a subsystem in ways that cannot be described by projective measurement on the subsystem alone. They are used in the field of quantum information
. Quantum t-designs have been recently introduced to POVMs and SIC-POVMs as a means of providing a simple and elegant formulation of the field in a general setting, since a SIC-POVM is a type of spherical t-design.
In rough analogy, a POVM is to a projective measurement what a density matrix
is to a pure state. Density matrices can describe part of a larger system that is in a pure state (see purification of quantum state
); analogously, POVMs on a physical system can describe the effect of a projective measurement performed on a larger system.
positive semidefinite operators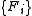
on a Hilbert space 
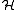that sum to unity,
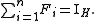
This formula is similar to the decomposition of a Hilbert space
by a set of orthogonal projectors:
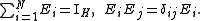
An important difference is that the elements of a POVM are not necessarily orthogonal, with the consequence that the number of elements in the POVM, n, can be larger than the dimension, N, of the Hilbert space
they act in.
In general, POVMs can be defined in situations where outcomes can occur in a non-discrete space. The relevant fact is that measurements determine probability measures on the outcome space:
Definition. Let (X, M) be measurable space; that is M is a σ-algebra of subsets of X. A POVM is a function F defined on M whose values are bounded non-negative self-adjoint operators on a Hilbert space H such that F(X) = IH and for every ξ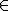
H,
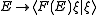
is a non-negative countably additive measure on the σ-algebra M.
This definition should be contrasted with that for the projection-valued measure
, which is very similar, except that, in the projection-valued measure, the F are required to be projection operators.
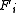occurs is
where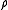
is the density matrix of the measured system.
Such a measurement can be carried out by doing a projective measurement in a larger Hilbert space. Let us extend the Hilbert space
to 
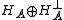and perform the measurement defined by the projection operators 
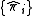. The probability of the outcome associated with 
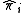is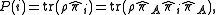
where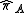
is the orthogonal projection taking 
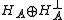to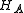 
. In the original Hilbert space 
, this is a POVM with operators given by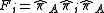 
. Neumark's dilation theorem guarantees that any POVM can be implemented in this manner.
In practice, POVMs are usually performed by coupling the original system to an ancilla. For an ancilla prepared in a pure state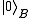
, this is a special case of the above; the Hilbert space is extended by the states 
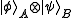where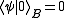 
.
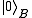. We entangle the ancilla with the system, taking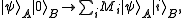
and perform a projective measurement on the ancilla in the
basis. The operators of the resulting POVM are given by
.
Since the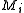
are not required to be positive, there are an infinite number of solutions to this equation. This means that there are infinite different experimental apparatuses that give the same probabilities for the outcomes. Since the post-measurement state of the system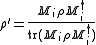
depends on the
, in general it cannot be inferred from the POVM alone.
Another difference from the projective measurements is that a POVM is not repeatable. If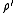
is subjected to the same measurement, the new state is
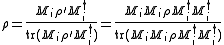
which is equal to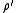
iff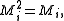 
that is, if the POVM reduces to a projective measurement.
This gives rises to many interesting effects, amongst them the quantum anti-Zeno effect
.
Neumark's dilation theorem
is the classification result for POVM's. It states that a POVM can be "lifted" by an operator map of the form V*(·)V to a projection-valued measure. In the physical context, this means that measuring a POVM consisting of a set of n > N rank-one operators acting on a N-dimensional Hilbert space
can always be achieved by performing a projective measurement on a Hilbert space of dimension n.
. This one is the main tool of the retrodictive approach of quantum physics in which we make predictions about state preparations leading to a measurement result.
We show, that this state simply corresponds to the normalized POVM element:
We can make predictions about preparations leading to the result 'n' by using an expression similar to Born's rule
:
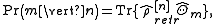
in which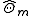
is a hermitian and positive operator corresponding to a proposition about the state of the measured system just after its preparation in some a state 
.
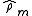Such an approach allows us to determine in which kind of states the system was prepared for leading to the result 'n'.
Thus, the non-classicality of a measurement corresponds to the non-classicality of its pre-measurement state, for which such a notion can be measured by different signatures of non-classicality.
The projective character of a measurement can be measured by its projectivity
which is the purity of its pre-measurement state:
The measurement is projective when its pre-measurement state is a pure quantum state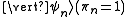
. Thus, the corresponding POVM element is given by:
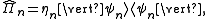
where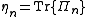
is in fact the detection efficiency of the state 
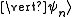, since Born's rule
leads to
.
Therefore, the measurement can be projective but non-ideal, which is an important distinction with the usual definition of projective measurements.
protocols such as quantum cryptography
, quantum coin-flipping, and quantum money
. This example will show that a POVM has a higher success probability for performing UQSD than any possible projective measurement.
First let us consider a trivial case. Take a set that consists of two orthogonal states
and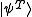
. A projective measurement of the form,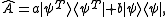
will result in eigenvalue a only when the system is in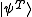
and eigenvalue b only when the system is in 
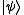. In addition, the measurement always discriminates between the two states (i.e. with 100% probability). This latter ability is unnecessary for UQSD and, in fact, is impossible for anything but orthogonal states.
Now consider a set that consists of two states
and 
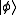in two-dimensional Hilbert space that are not orthogonal. i.e.,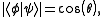
for
. These could be states of a system such as the spin
of spin-1/2 particle (e.g. an electron), or the polarization
of a photon
. Assuming that the system has an equal likelihood of being in each of these two states, the best strategy for UQSD using only projective measurement is to perform each of the following measurements,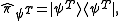
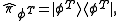
50% of the time. If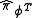
is measured and results in an eigenvalue of 1, than it is certain that the state must have been in 
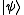. However, an eigenvalue of zero is now an inconclusive result since this can come about from the system could being in either of the two states in the set. Similarly, a result of 1 for 
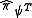indicates conclusively that the system is in 
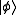and 0 is inconclusive. The probability that this strategy returns a conclusive result is,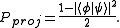
In contrast, a strategy based on POVMs has a greater probability of success given by,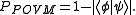
This is the minimum allowed by the rules of quantum indeterminacy
and the uncertainty principle
. This strategy is based on a POVM consisting of,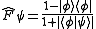
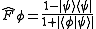
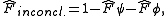
where the result associated with
indicates the system is in state i with certainty.
These POVMs can be created by extending the two-dimensional Hilbert space. This can be visualized as follows: The two states fall in the x-y plane with an angle of θ between them and the space is extended in the z-direction. (The total space is the direct sum
of spaces defined by the z-direction and the x-y plane.) The measurement first unitarily
rotates the states towards the z-axis so that
has no component along the y-direction and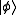 
has no component along the x-direction. At this point, the three elements of the POVM correspond to projective measurements along x-direction, y-direction and z-direction, respectively.
For a specific example, take a stream of photons, each of which are polarized along either the horizontal direction or at 45 degrees. On average there are equal numbers of horizontal and 45 degree photons. The projective strategy corresponds to passing the photons through a polarizer in either the vertical direction or -45 degree direction. If the photon passes through the vertical polarizer it must have been at 45 degrees and vice versa. The success probability is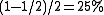
. The POVM strategy for this example is more complicated and requires another optical mode
(known as an ancilla
). It has a success probability of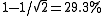
.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and quantum measurement theory, a POVM (Positive Operator Valued Measure) is a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
whose values are non-negative self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
s on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. It is the most general formulation of a measurement in the theory of quantum physics. The need for the POVM formalism arises from the fact that projective measurements on a larger system will act on a subsystem in ways that cannot be described by projective measurement on the subsystem alone. They are used in the field of quantum information
Quantum information
In quantum mechanics, quantum information is physical information that is held in the "state" of a quantum system. The most popular unit of quantum information is the qubit, a two-level quantum system...
. Quantum t-designs have been recently introduced to POVMs and SIC-POVMs as a means of providing a simple and elegant formulation of the field in a general setting, since a SIC-POVM is a type of spherical t-design.
In rough analogy, a POVM is to a projective measurement what a density matrix
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
is to a pure state. Density matrices can describe part of a larger system that is in a pure state (see purification of quantum state
Purification of quantum state
In quantum mechanics, especially quantum information, purification refers to the fact that every mixed state acting on finite dimensional Hilbert spaces can be viewed as the reduced state of some pure state....
); analogously, POVMs on a physical system can describe the effect of a projective measurement performed on a larger system.
Definition
In the simplest case, a POVM is a set of HermitianHermitian
A number of mathematical entities are named Hermitian, after the mathematician Charles Hermite:*Hermitian adjoint*Hermitian connection, the unique connection on a Hermitian manifold that satisfies specific conditions...
positive semidefinite operators
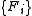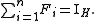
on a Hilbert space that sum to unity,This formula is similar to the decomposition of a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
by a set of orthogonal projectors:
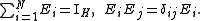
An important difference is that the elements of a POVM are not necessarily orthogonal, with the consequence that the number of elements in the POVM, n, can be larger than the dimension, N, of the Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
they act in.
In general, POVMs can be defined in situations where outcomes can occur in a non-discrete space. The relevant fact is that measurements determine probability measures on the outcome space:
Definition. Let (X, M) be measurable space; that is M is a σ-algebra of subsets of X. A POVM is a function F defined on M whose values are bounded non-negative self-adjoint operators on a Hilbert space H such that F(X) = IH and for every ξ
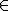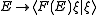
H,is a non-negative countably additive measure on the σ-algebra M.
This definition should be contrasted with that for the projection-valued measure
Projection-valued measure
In mathematics, particularly functional analysis a projection-valued measure is a function defined on certain subsets of a fixed set and whose values are self-adjoint projections on a Hilbert space...
, which is very similar, except that, in the projection-valued measure, the F are required to be projection operators.
POVMs and measurement
As in the theory of projective measurement, the probability the outcome associated with measurement of operator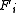 occurs iswhere
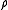is the density matrix of the measured system.Such a measurement can be carried out by doing a projective measurement in a larger Hilbert space. Let us extend the Hilbert space
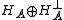to and perform the measurement defined by the projection operators 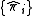. The probability of the outcome associated with 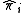is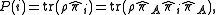where
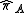is the orthogonal projection taking 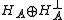to 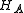. In the original Hilbert space , this is a POVM with operators given by 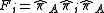. Neumark's dilation theorem guarantees that any POVM can be implemented in this manner.In practice, POVMs are usually performed by coupling the original system to an ancilla. For an ancilla prepared in a pure state
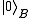, this is a special case of the above; the Hilbert space is extended by the states 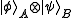where 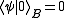.Post-measurement state
Consider the case where the ancilla is initially a pure state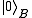. We entangle the ancilla with the system, taking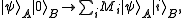and perform a projective measurement on the ancilla in the
basis. The operators of the resulting POVM are given by.Since the
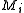are not required to be positive, there are an infinite number of solutions to this equation. This means that there are infinite different experimental apparatuses that give the same probabilities for the outcomes. Since the post-measurement state of the system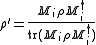depends on the
, in general it cannot be inferred from the POVM alone.Another difference from the projective measurements is that a POVM is not repeatable. If
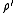is subjected to the same measurement, the new state is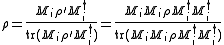which is equal to
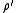iff 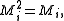that is, if the POVM reduces to a projective measurement.This gives rises to many interesting effects, amongst them the quantum anti-Zeno effect
Quantum Zeno effect
The quantum Zeno effect is a name coined by George Sudarshan and Baidyanath Misra of the University of Texas in 1977 in their analysis of the situation in which an unstable particle, if observed continuously, will never decay. One can nearly "freeze" the evolution of the system by measuring it...
.
Neumark's dilation theorem
- Note: An alternate spelling of this is "Naimark's Theorem"
Neumark's dilation theorem
Naimark's dilation theorem
In operator theory, Naimark's dilation theorem is a result that characterizes positive operator valued measures. It can be viewed as a consequence of Stinespring's dilation theorem.- Note :...
is the classification result for POVM's. It states that a POVM can be "lifted" by an operator map of the form V*(·)V to a projection-valued measure. In the physical context, this means that measuring a POVM consisting of a set of n > N rank-one operators acting on a N-dimensional Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
can always be achieved by performing a projective measurement on a Hilbert space of dimension n.
Quantum properties of measurements
A recent work shows that the properties of a measurement are not revealed by the POVM element corresponding to the measurement, but by its pre-measurement stateQuantum tomography
Quantum tomography or quantum state tomography is the process of reconstructing the quantum state for a source of quantum systems by measurements on the systems coming from the source. The source may be any device or system which prepares quantum states either consistently into quantum pure states...
. This one is the main tool of the retrodictive approach of quantum physics in which we make predictions about state preparations leading to a measurement result.
We show, that this state simply corresponds to the normalized POVM element:
We can make predictions about preparations leading to the result 'n' by using an expression similar to Born's rule
Born rule
The Born rule is a law of quantum mechanics which gives the probability that a measurement on a quantum system will yield a given result. It is named after its originator, the physicist Max Born. The Born rule is one of the key principles of quantum mechanics...
:
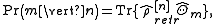
in which
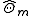is a hermitian and positive operator corresponding to a proposition about the state of the measured system just after its preparation in some a state 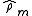.Such an approach allows us to determine in which kind of states the system was prepared for leading to the result 'n'.
Thus, the non-classicality of a measurement corresponds to the non-classicality of its pre-measurement state, for which such a notion can be measured by different signatures of non-classicality.
The projective character of a measurement can be measured by its projectivity
which is the purity of its pre-measurement state:The measurement is projective when its pre-measurement state is a pure quantum state
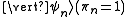. Thus, the corresponding POVM element is given by: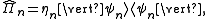where
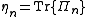is in fact the detection efficiency of the state 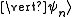, since Born's ruleBorn rule
The Born rule is a law of quantum mechanics which gives the probability that a measurement on a quantum system will yield a given result. It is named after its originator, the physicist Max Born. The Born rule is one of the key principles of quantum mechanics...
leads to
.Therefore, the measurement can be projective but non-ideal, which is an important distinction with the usual definition of projective measurements.
An example: Unambiguous quantum state discrimination
The task of unambiguous quantum state discrimination (UQSD) is to discern conclusively which state, of given set of pure states, a quantum system (which we call the input) is in. The impossibility of perfectly discriminating between a set of non-orthogonal states is the basis for quantum informationQuantum information
In quantum mechanics, quantum information is physical information that is held in the "state" of a quantum system. The most popular unit of quantum information is the qubit, a two-level quantum system...
protocols such as quantum cryptography
Quantum cryptography
Quantum key distribution uses quantum mechanics to guarantee secure communication. It enables two parties to produce a shared random secret key known only to them, which can then be used to encrypt and decrypt messages...
, quantum coin-flipping, and quantum money
Quantum money
Quantum Money is a proposed design of bank notes making them impossible to forge, by using quantum physics. The idea influenced the development of quantum key distribution protocols used in quantum cryptography....
. This example will show that a POVM has a higher success probability for performing UQSD than any possible projective measurement.
First let us consider a trivial case. Take a set that consists of two orthogonal states
and
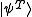. A projective measurement of the form,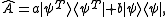will result in eigenvalue a only when the system is in
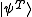and eigenvalue b only when the system is in 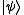. In addition, the measurement always discriminates between the two states (i.e. with 100% probability). This latter ability is unnecessary for UQSD and, in fact, is impossible for anything but orthogonal states.Now consider a set that consists of two states
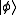and in two-dimensional Hilbert space that are not orthogonal. i.e.,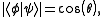for
. These could be states of a system such as the spinSpin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
of spin-1/2 particle (e.g. an electron), or the polarization
Photon polarization
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. Individual photons are completely polarized...
of a photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
. Assuming that the system has an equal likelihood of being in each of these two states, the best strategy for UQSD using only projective measurement is to perform each of the following measurements,
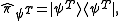
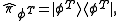
50% of the time. If
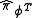is measured and results in an eigenvalue of 1, than it is certain that the state must have been in 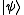. However, an eigenvalue of zero is now an inconclusive result since this can come about from the system could being in either of the two states in the set. Similarly, a result of 1 for 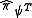indicates conclusively that the system is in 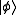and 0 is inconclusive. The probability that this strategy returns a conclusive result is,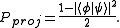In contrast, a strategy based on POVMs has a greater probability of success given by,
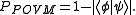
This is the minimum allowed by the rules of quantum indeterminacy
Quantum indeterminacy
Quantum indeterminacy is the apparent necessary incompleteness in the description of a physical system, that has become one of the characteristics of the standard description of quantum physics...
and the uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
. This strategy is based on a POVM consisting of,
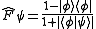
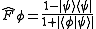
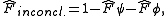
where the result associated with
indicates the system is in state i with certainty.These POVMs can be created by extending the two-dimensional Hilbert space. This can be visualized as follows: The two states fall in the x-y plane with an angle of θ between them and the space is extended in the z-direction. (The total space is the direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of spaces defined by the z-direction and the x-y plane.) The measurement first unitarily
Unitary
Unitary may refer to:* Unitary construction, in automotive design, another common term for a unibody or monocoque construction**Unitary as chemical weapons opposite of Binary...
rotates the states towards the z-axis so that
has no component along the y-direction and 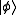has no component along the x-direction. At this point, the three elements of the POVM correspond to projective measurements along x-direction, y-direction and z-direction, respectively.For a specific example, take a stream of photons, each of which are polarized along either the horizontal direction or at 45 degrees. On average there are equal numbers of horizontal and 45 degree photons. The projective strategy corresponds to passing the photons through a polarizer in either the vertical direction or -45 degree direction. If the photon passes through the vertical polarizer it must have been at 45 degrees and vice versa. The success probability is
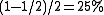. The POVM strategy for this example is more complicated and requires another optical modeTransverse mode
A transverse mode of a beam of electromagnetic radiation is a particular electromagnetic field pattern of radiation measured in a plane perpendicular to the propagation direction of the beam...
(known as an ancilla
Ancilla
Ancilla may refer to:* Ancilla College* Ancilla * Ancilla - a genus of Olive shells* Ancilla Dei, a title given to a deceased woman in early Christian inscriptions....
). It has a success probability of
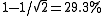.See also
- Quantum measurement
- Mathematical formulation of quantum mechanicsMathematical formulation of quantum mechanicsThe mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. Such are distinguished from mathematical formalisms for theories developed prior to the early 1900s by the use of abstract mathematical structures, such as...
- Quantum logicQuantum logicIn quantum mechanics, quantum logic is a set of rules for reasoning about propositions which takes the principles of quantum theory into account...
- Density matrixDensity matrixIn quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
- Quantum operationQuantum operationIn quantum mechanics, a quantum operation is a mathematical formalism used to describe a broad class of transformations that a quantum mechanical system can undergo. This was first discussed as a general stochastic transformation for a density matrix by George Sudarshan...
- Projection-valued measureProjection-valued measureIn mathematics, particularly functional analysis a projection-valued measure is a function defined on certain subsets of a fixed set and whose values are self-adjoint projections on a Hilbert space...
- Vector measureVector measureIn mathematics, a vector measure is a function defined on a family of sets and taking vector values satisfying certain properties. It is a generalization of the concept of measure, which takes nonnegative real values only.-Definitions and first consequences:...