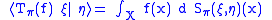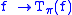Projection-valued measure
Encyclopedia
In mathematics
, particularly functional analysis
a projection-valued measure (PVM) is a function defined on certain subsets of a fixed set and whose values are self-adjoint projections on a Hilbert space
. Projection-valued measures are used to express results in spectral theory
, such as the spectral theorem for self-adjoint operator
s.
(X, M), where M is a σ-algebra of subsets of X, is a mapping
π from M to the set of self-adjoint
projections on a Hilbert space
H such that
and for every ξ, η ∈ H, the set-function
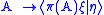
is a complex measure
on M (that is, a complex-valued countably additive
function). We denote this measure by .
.
If π is a projection-valued measure and
then π(A), π(B) are orthogonal projections. From this follows that in general,
Example. Suppose (X, M, μ) is a measure space. Let π(A) be the operator of multiplication by the indicator function 1A on L2(X)
. Then π is a projection-valued measure.
extends to a linear map on the vector space of step function
s on X. In fact, it is easy to check that this map is a ring homomorphism. In fact this map extends in a canonical way to all bounded complex-valued Borel functions on X.
Theorem. For any bounded M-measurable function f on X, there is a unique bounded linear operator Tπ(f) such that
for all ξ, η ∈ H. The map
is a homomorphism of rings.
s. Suppose (X, M, μ) is a measure space and let {Hx}x ∈ X be a μ-measurable family of separable Hilbert spaces. For every A ∈ M, let π(A) be the operator of multiplication by 1A on the Hilbert space

Then π is a projection-valued measure on (X, M).
Suppose π, ρ are projection-valued measures on (X, M) with values in the projections of H, K. π, ρ are unitarily equivalent if and only if
there is a unitary operator U:H → K such that

for every A ∈ M.
Theorem. If (X, M) is a standard Borel space, then for every projection-valued measure π on (X, M) taking values in the projections of a separable Hilbert space, there is a Borel measure μ and a μ-measurable family of Hilbert spaces {Hx}x ∈ X , such that π is unitarily equivalent to multiplication by 1A on the Hilbert space
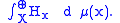
The measure class of μ and the measure equivalence class of the multiplicity function x → dim Hx completely characterize the projection-valued measure up to unitary equivalence.
A projection-valued measure π is homogeneous of multiplicity n if and only if the multiplicity function has constant value n. Clearly,
Theorem. Any projection-valued measure π taking values in the projections of a separable Hilbert space is an orthogonal direct sum of homogeneous projection-valued measures:

where

and

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
a projection-valued measure (PVM) is a function defined on certain subsets of a fixed set and whose values are self-adjoint projections on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. Projection-valued measures are used to express results in spectral theory
Spectral theory
In mathematics, spectral theory is an inclusive term for theories extending the eigenvector and eigenvalue theory of a single square matrix to a much broader theory of the structure of operators in a variety of mathematical spaces. It is a result of studies of linear algebra and the solutions of...
, such as the spectral theorem for self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
s.
Formal definition
A projection-valued measure on a measurable space(X, M), where M is a σ-algebra of subsets of X, is a mapping
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
π from M to the set of self-adjoint
Self-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
projections on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H such that
and for every ξ, η ∈ H, the set-function
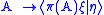
is a complex measure
Complex measure
In mathematics, specifically measure theory, a complex measure generalizes the concept of measure by letting it have complex values. In other words, one allows for sets whose size is a complex number.-Definition:...
on M (that is, a complex-valued countably additive
Sigma additivity
In mathematics, additivity and sigma additivity of a function defined on subsets of a given set are abstractions of the intuitive properties of size of a set.- Additive set functions :...
function). We denote this measure by
 .
.If π is a projection-valued measure and
then π(A), π(B) are orthogonal projections. From this follows that in general,
Example. Suppose (X, M, μ) is a measure space. Let π(A) be the operator of multiplication by the indicator function 1A on L2(X)
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
. Then π is a projection-valued measure.
Extensions of projection-valued measures
If π is an additive projection-valued measure on (X, M), then the mapextends to a linear map on the vector space of step function
Step function
In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals...
s on X. In fact, it is easy to check that this map is a ring homomorphism. In fact this map extends in a canonical way to all bounded complex-valued Borel functions on X.
Theorem. For any bounded M-measurable function f on X, there is a unique bounded linear operator Tπ(f) such that
for all ξ, η ∈ H. The map
is a homomorphism of rings.
Structure of projection-valued measures
First we provide a general example of projection-valued measure based on direct integralDirect integral
In mathematics and functional analysis a direct integral is a generalization of the concept of direct sum. The theory is most developed for direct integrals of Hilbert spaces and direct integrals of von Neumann algebras. The concept was introduced in 1949 by John von Neumann in one of the papers...
s. Suppose (X, M, μ) is a measure space and let {Hx}x ∈ X be a μ-measurable family of separable Hilbert spaces. For every A ∈ M, let π(A) be the operator of multiplication by 1A on the Hilbert space

Then π is a projection-valued measure on (X, M).
Suppose π, ρ are projection-valued measures on (X, M) with values in the projections of H, K. π, ρ are unitarily equivalent if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there is a unitary operator U:H → K such that

for every A ∈ M.
Theorem. If (X, M) is a standard Borel space, then for every projection-valued measure π on (X, M) taking values in the projections of a separable Hilbert space, there is a Borel measure μ and a μ-measurable family of Hilbert spaces {Hx}x ∈ X , such that π is unitarily equivalent to multiplication by 1A on the Hilbert space
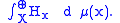
The measure class of μ and the measure equivalence class of the multiplicity function x → dim Hx completely characterize the projection-valued measure up to unitary equivalence.
A projection-valued measure π is homogeneous of multiplicity n if and only if the multiplicity function has constant value n. Clearly,
Theorem. Any projection-valued measure π taking values in the projections of a separable Hilbert space is an orthogonal direct sum of homogeneous projection-valued measures:

where

and