LOCC
Encyclopedia
LOCC, or Local Operations and Classical Communication, is a method in quantum information theory where a local (product) operation is performed on part of the system, and where the result of that operation is "communicated" classically to another part where usually another local operation is performed. An example of this is distinguishing two Bell pairs
, such as the following:
Let's say the two-qubit
system is separated, where the first qubit is given to Alice and the second is given to Bob. Assume that Alice measures the first qubit, and obtains the result 0. We still don't know which Bell pair we were given. Alice sends the result to Bob over a classical channel, where Bob measures the second qubit, also obtaining 0. Bob now knows that since the joint measurement outcome is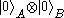
, then the pair given was 
.
These measurements contrasts with nonlocal or entangled measurements, where a single measurement is performed in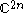
instead of the product space 
.
Consider two particles in a Hilbert space of dimension d with particle states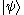
and 
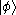with Schmidt decomposition
s
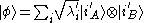
The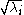
's are known as Schmidt coefficients
. If they are ordered largest to smallest (i.e. with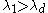
) then 
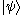can only be transformed into 
using only local operations if and only if for all 
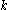in the range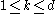 
In more concise notation:
This is a more restrictive condition that local operations cannot increase the degree of entanglement. It is quite possible that converting between
and 
in either direction is impossible because neither set of Schmidt coefficients majorises the other. For large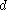 
if all Schmidt coefficients
are non-zero then the probability of one set of coefficients majorising the other becomes negligible. Therefore for large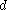
the probability of any arbitrary state being converted into another becomes negligible.
Bell state
The Bell states are a concept in quantum information science and represent the simplest possible examples of entanglement. They are named after John S. Bell, as they are the subject of his famous Bell inequality. An EPR pair is a pair of qubits which jointly are in a Bell state, that is, entangled...
, such as the following:
Let's say the two-qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
system is separated, where the first qubit is given to Alice and the second is given to Bob. Assume that Alice measures the first qubit, and obtains the result 0. We still don't know which Bell pair we were given. Alice sends the result to Bob over a classical channel, where Bob measures the second qubit, also obtaining 0. Bob now knows that since the joint measurement outcome is
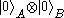, then the pair given was .These measurements contrasts with nonlocal or entangled measurements, where a single measurement is performed in
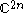instead of the product space .Entanglement manipulation
Nielsen has derived a general condition to determine whether one state of a bipartite quantum system may be transformed into another using only LOCC. Full details may be found in the paper referenced earlier, the results are sketched out here.Consider two particles in a Hilbert space of dimension d with particle states
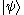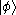and with Schmidt decompositionSchmidt decomposition
In linear algebra, the Schmidt decomposition refers to a particular way of expressing a vector in the tensor product of two inner product spaces. It has applications in quantum information theory and plasticity....
s
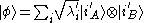
The
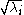's are known as Schmidt coefficientsSchmidt decomposition
In linear algebra, the Schmidt decomposition refers to a particular way of expressing a vector in the tensor product of two inner product spaces. It has applications in quantum information theory and plasticity....
. If they are ordered largest to smallest (i.e. with
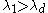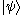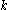) then can only be transformed into using only local operations if and only if for all in the range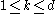 In more concise notation:
This is a more restrictive condition that local operations cannot increase the degree of entanglement. It is quite possible that converting between
and in either direction is impossible because neither set of Schmidt coefficients majorises the other. For large 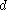if all Schmidt coefficientsSchmidt decomposition
In linear algebra, the Schmidt decomposition refers to a particular way of expressing a vector in the tensor product of two inner product spaces. It has applications in quantum information theory and plasticity....
are non-zero then the probability of one set of coefficients majorising the other becomes negligible. Therefore for large
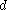the probability of any arbitrary state being converted into another becomes negligible.Further reading
- http://www.quantiki.org/wiki/index.php/LOCC_operations
- M. A. Nielsen, “Conditions for a class of entanglement transformations”, Phys. Rev. Lett. 83 (2) 436-439 (1999) (http://arxiv.org/abs/quant-ph/9811053)