Weyl-Brauer matrices
Encyclopedia
In mathematics
, particularly in the theory of spinor
s, the Weyl–Brauer matrices are an explicit realization of a Clifford algebra
as a matrix algebra
. They generalize in n dimensions as the Pauli matrices
. They are named for Richard Brauer
and Hermann Weyl
, and were one of the first attempts to approach systematically the problem of spinors from a representation theoretic
standpoint.
The matrices are formed by taking tensor product
s of the Pauli matrices, and the space of spinors may then be realized as the column vectors on which the Weyl–Brauer matrices act.
of dimension n. There is a sharp contrast in the construction of the Weyl–Brauer matrices depending on whether the dimension n is even or odd. Let n = 2k or 2k + 1, and suppose that the Euclidean quadratic form
on V is given by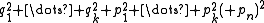
where (pi, qi) are the standard coordinates on Rn.
Define matrices 1, 1', P, and Q by
.
In even or in odd dimensionality, this quantization procedure amounts to replacing the ordinary p, q coordinates with non-commutative coordinates constructed from P, Q in a suitable fashion. P and Q correspond to the generalized "position" and "momentum" for the Weyl quantization
, but this physical fact is not important for the abstract construction of the spinors.
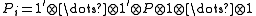
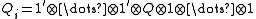
for i = 1,2,...,k (where the P or Q is considered to occupy the i-th position). The operation
is the tensor product
of matrices. It is no longer important to distinguish between the Ps and Qs, so we shall simply refer to them all with the symbol P, and regard the index on Pi as ranging from i = 1 to i = 2k. For instance, the following properties hol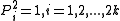d:
, and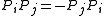 
for all unequal pairs i and j. (Clifford relations.)
Thus the algebra generated by the Pi is the Clifford algebra
of euclidean n-space.
Let A denote the algebra generated by these matrices. By counting dimensions, A is a complete 2k×2k matrix algebra over the complex numbers. As a matrix algebra, therefore, it acts on 2k-dimensional column vectors (with complex entries). These column vectors are the spinors.
We now turn to the action of the orthogonal group on the spinors. Consider the application of an orthogonal transformation to the coordinates, which in turn acts upon the Pi via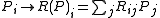
.
Since the Pi generate A, the action of this transformation extends to all of A and produces an automorphism
of A. From elementary linear algebra, any such automorphism must be given by a change of basis
. Hence there is a matrix S, depending on R, such that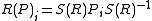
(1).
In particular, S(R) will act on column vectors (spinors). By decomposing rotations into products of reflections, one can write down a formula for S(R) in much the same way as in the case of three dimensions.
However, just as in the three-dimensional case, there will be more than one matrix S(R) which produces the action in (1). The ambiguity defines S(R) up to a nonevanescent scalar factor c. Since S(R) and cS(R) define the same transformation (1), the action of the orthogonal group on spinors is not single-valued, but instead descends to an action on the projective space
associated to the space of spinors. This multiple-valued action can be sharpened by normalizing the constant c in such a way that (det S(R))2 = 1. In order to do this, however, it is necessary to discuss how the space of spinors (column vectors) may be identified with its dual (row vectors).
In order to identify spinors with their duals, let C be the matrix defined by
Then conjugation by C converts a Pi matrix to its transpose: tPi = C Pi C−1. Under the action of a rotation,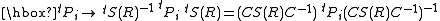
whence C S(R) C−1 = α tS(R)−1 for some scalar α. The scalar factor α can be made to equal one by rescaling S(R). Under these circumstances, (det S(R))2 = 1, as required.
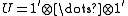, (k factors).
Then U is preserved under rotations, so in particular its eigenspace decomposition (which necessarily corresponds to the eigenvalues +1 and -1, occurring in equal numbers) is also stabilized by rotations. As a consequence, each spinor admits a decomposition into eigenvectors under U:
into a right-handed Weyl spinor ξ+ and a left-handed Weyl spinor ξ-. Because rotations preserve the eigenspaces of U, the rotations themselves act diagonally as matrices S(R)+, S(R)- viaξ)+ = S+(R) ξ+, andξ)- = S-(R) ξ-.
This decomposition is not, however, stable under improper rotation
s (e.g., reflections in a hyperplane). A reflection in a hyperplane has the effect of interchanging the two eigenspaces. Thus there are two irreducible spin representations in even dimensions given by the left-handed and right-handed Weyl spinors, each of which has dimension 2k-1. However, there is only one irreducible pin representation (see below) owing to the non-invariance of the above eigenspace decomposition under improper rotations, and that has dimension 2k.
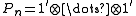, (k factors),
so that the Clifford relations still hold. This adjunction has no effect on the algebra A of matrices generated by the Pi, since in either case A is still a complete matrix algebra of the same dimension. Thus A, which is a complete 2k×2k matrix algebra, is not the Clifford algebra, which is an algebra of dimension 2×2k×2k. Rather A is the quotient of the Clifford algebra by a certain ideal.
Nevertheless, one can show that if R is a proper rotation (an orthogonal transformation of determinant one), then the rotation among the coordinates
is again an automorphism of A, and so induces a change of basis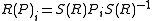
exactly as in the even dimensional case. The projective representation S(R) may again be normalized so that (det S(R))2 = 1. It may further be extended to general orthogonal transformations by setting S(R) = -S(-R) in case det R = -1 (i.e., if R is a reversal).
In the case of odd dimensions it is not possible to split a spinor into a pair of Weyl spinors, and spinors form an irreducible representation of the spin group. As in the even case, it is possible to identify spinors with their duals, but for one caveat. The identification of the space of spinors with its dual space is invariant under proper rotations, and so the two spaces are spinorially equivalent. However, if improper rotations are also taken into consideration, then the spin space and its dual are not isomorphic. Thus, while there is only one spin representation in odd dimensions, there are a pair of inequivalent pin representations. This fact is not evident from the Weyl's quantization approach, however, and is more easily seen by considering the representations of the full Clifford algebra.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly in the theory of spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s, the Weyl–Brauer matrices are an explicit realization of a Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
as a matrix algebra
Matrix algebra
Matrix algebra may refer to:*Matrix theory, is the branch of mathematics that studies matrices*Matrix ring, thought of as an algebra over a field or a commutative ring...
. They generalize in n dimensions as the Pauli matrices
Pauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
. They are named for Richard Brauer
Richard Brauer
Richard Dagobert Brauer was a leading German and American mathematician. He worked mainly in abstract algebra, but made important contributions to number theory...
and Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
, and were one of the first attempts to approach systematically the problem of spinors from a representation theoretic
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
standpoint.
The matrices are formed by taking tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
s of the Pauli matrices, and the space of spinors may then be realized as the column vectors on which the Weyl–Brauer matrices act.
Construction
Suppose that V = Rn is a Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
of dimension n. There is a sharp contrast in the construction of the Weyl–Brauer matrices depending on whether the dimension n is even or odd. Let n = 2k or 2k + 1, and suppose that the Euclidean quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
on V is given by
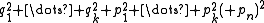
where (pi, qi) are the standard coordinates on Rn.
Define matrices 1, 1', P, and Q by
.In even or in odd dimensionality, this quantization procedure amounts to replacing the ordinary p, q coordinates with non-commutative coordinates constructed from P, Q in a suitable fashion. P and Q correspond to the generalized "position" and "momentum" for the Weyl quantization
Weyl quantization
In mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
, but this physical fact is not important for the abstract construction of the spinors.
Even case
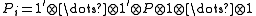
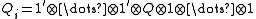
In the case when n = 2k is even, letfor i = 1,2,...,k (where the P or Q is considered to occupy the i-th position). The operation
is the tensor productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of matrices. It is no longer important to distinguish between the Ps and Qs, so we shall simply refer to them all with the symbol P, and regard the index on Pi as ranging from i = 1 to i = 2k. For instance, the following properties hold:
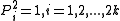, and 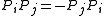for all unequal pairs i and j. (Clifford relations.)Thus the algebra generated by the Pi is the Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
of euclidean n-space.
Let A denote the algebra generated by these matrices. By counting dimensions, A is a complete 2k×2k matrix algebra over the complex numbers. As a matrix algebra, therefore, it acts on 2k-dimensional column vectors (with complex entries). These column vectors are the spinors.
We now turn to the action of the orthogonal group on the spinors. Consider the application of an orthogonal transformation to the coordinates, which in turn acts upon the Pi via
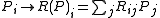.Since the Pi generate A, the action of this transformation extends to all of A and produces an automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of A. From elementary linear algebra, any such automorphism must be given by a change of basis
Change of basis
In linear algebra, change of basis refers to the conversion of vectors and linear transformations between matrix representations which have different bases.-Expression of a basis:...
. Hence there is a matrix S, depending on R, such that
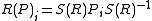(1).In particular, S(R) will act on column vectors (spinors). By decomposing rotations into products of reflections, one can write down a formula for S(R) in much the same way as in the case of three dimensions.
However, just as in the three-dimensional case, there will be more than one matrix S(R) which produces the action in (1). The ambiguity defines S(R) up to a nonevanescent scalar factor c. Since S(R) and cS(R) define the same transformation (1), the action of the orthogonal group on spinors is not single-valued, but instead descends to an action on the projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
associated to the space of spinors. This multiple-valued action can be sharpened by normalizing the constant c in such a way that (det S(R))2 = 1. In order to do this, however, it is necessary to discuss how the space of spinors (column vectors) may be identified with its dual (row vectors).
In order to identify spinors with their duals, let C be the matrix defined by
Then conjugation by C converts a Pi matrix to its transpose: tPi = C Pi C−1. Under the action of a rotation,
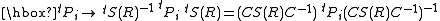
whence C S(R) C−1 = α tS(R)−1 for some scalar α. The scalar factor α can be made to equal one by rescaling S(R). Under these circumstances, (det S(R))2 = 1, as required.
Weyl spinors
Let U be the element of the algebra A defined by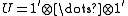, (k factors).Then U is preserved under rotations, so in particular its eigenspace decomposition (which necessarily corresponds to the eigenvalues +1 and -1, occurring in equal numbers) is also stabilized by rotations. As a consequence, each spinor admits a decomposition into eigenvectors under U:
- ξ = ξ+ + ξ-
into a right-handed Weyl spinor ξ+ and a left-handed Weyl spinor ξ-. Because rotations preserve the eigenspaces of U, the rotations themselves act diagonally as matrices S(R)+, S(R)- viaξ)+ = S+(R) ξ+, andξ)- = S-(R) ξ-.
This decomposition is not, however, stable under improper rotation
Improper rotation
In 3D geometry, an improper rotation, also called rotoreflection or rotary reflection is, depending on context, a linear transformation or affine transformation which is the combination of a rotation about an axis and a reflection in a plane perpendicular to the axis.Equivalently it is the...
s (e.g., reflections in a hyperplane). A reflection in a hyperplane has the effect of interchanging the two eigenspaces. Thus there are two irreducible spin representations in even dimensions given by the left-handed and right-handed Weyl spinors, each of which has dimension 2k-1. However, there is only one irreducible pin representation (see below) owing to the non-invariance of the above eigenspace decomposition under improper rotations, and that has dimension 2k.
Odd case
In the quantization for an odd number 2k+1 of dimensions, the matrices Pi may be introduced as above for i = 1,2,...,2k, and the following matrix may be adjoined to the system: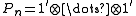, (k factors),so that the Clifford relations still hold. This adjunction has no effect on the algebra A of matrices generated by the Pi, since in either case A is still a complete matrix algebra of the same dimension. Thus A, which is a complete 2k×2k matrix algebra, is not the Clifford algebra, which is an algebra of dimension 2×2k×2k. Rather A is the quotient of the Clifford algebra by a certain ideal.
Nevertheless, one can show that if R is a proper rotation (an orthogonal transformation of determinant one), then the rotation among the coordinates
is again an automorphism of A, and so induces a change of basis
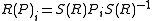
exactly as in the even dimensional case. The projective representation S(R) may again be normalized so that (det S(R))2 = 1. It may further be extended to general orthogonal transformations by setting S(R) = -S(-R) in case det R = -1 (i.e., if R is a reversal).
In the case of odd dimensions it is not possible to split a spinor into a pair of Weyl spinors, and spinors form an irreducible representation of the spin group. As in the even case, it is possible to identify spinors with their duals, but for one caveat. The identification of the space of spinors with its dual space is invariant under proper rotations, and so the two spaces are spinorially equivalent. However, if improper rotations are also taken into consideration, then the spin space and its dual are not isomorphic. Thus, while there is only one spin representation in odd dimensions, there are a pair of inequivalent pin representations. This fact is not evident from the Weyl's quantization approach, however, and is more easily seen by considering the representations of the full Clifford algebra.