
Windmill graph
Encyclopedia
In the mathematical
field of graph theory
, the windmill graph Wd(k,n) is a simple undirected graph with (k-1)n+1 vertices and nk(k−1)/2 edges. It is defined for k ≥ 2 and n ≥ 2.
The windmill graph Wd(k,n) can be constructed by joining n copies of the complete graph
Kk with a common vertex. It has girth 3 (if k > 2), radius 1 and diameter 2.
By removing the central vertex of the windmill graph, it can be proved that it is a 1-vertex-connected graph
. Each copy of the complete graph
Kk is (k-1)-edge-connected
graph. Therefore, the windmill graph is (k-1)-edge-connected. It is trivially perfect and a block graph
.
By construction, the windmill graph Wd(3,n) is the friendship graph
Fn, the windmill graph Wd(2,n) is the star graph
Sn and the windmill graph Wd(3,2) is the butterfly graph
.
can be deduced form the chromatic polynomial of the complete graph and is equal to
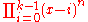
The windmill graph Wd(k,n) is proved not graceful
if k > 5. In 1979, Bermond has conjectured that Wd(4,n) is graceful for all n ≥ 4. This is known to be true for n ≤ 22. Bermond, Kotzig, and Turgeon proved that Wd(k,n) is not graceful when k = 4 and n = 2 or n = 3, and when k = 5 and m = 2. The windmill Wd(3,n) is graceful if and only if n ≡ 0 (mod 4) or n ≡ 1 (mod 4).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the windmill graph Wd(k,n) is a simple undirected graph with (k-1)n+1 vertices and nk(k−1)/2 edges. It is defined for k ≥ 2 and n ≥ 2.
The windmill graph Wd(k,n) can be constructed by joining n copies of the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
Kk with a common vertex. It has girth 3 (if k > 2), radius 1 and diameter 2.
By removing the central vertex of the windmill graph, it can be proved that it is a 1-vertex-connected graph
K-vertex-connected graph
In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
. Each copy of the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
Kk is (k-1)-edge-connected
K-edge-connected graph
In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....
graph. Therefore, the windmill graph is (k-1)-edge-connected. It is trivially perfect and a block graph
Block graph
In graph theory, a branch of combinatorial mathematics, a block graph is a type of undirected graph in which every biconnected component is a clique...
.
By construction, the windmill graph Wd(3,n) is the friendship graph
Friendship graph
In the mathematical field of graph theory, the friendship graph Fn is a planar undirected graph with 2n+1 vertices and 3n edges....
Fn, the windmill graph Wd(2,n) is the star graph
Star (graph theory)
In graph theory, a star Sk is the complete bipartite graph K1,k: a tree with one internal node and k leaves...
Sn and the windmill graph Wd(3,2) is the butterfly graph
Butterfly graph
In the mathematical field of graph theory, the butterfly graph is a planar undirected graph with 5 vertices and 6 edges...
.
Labeling and colouring
The windmill graph has chromatic number k and chromatic index n(k-1). Its chromatic polynomialChromatic polynomial
The chromatic polynomial is a polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to attack the four color problem. It was generalised to the Tutte...
can be deduced form the chromatic polynomial of the complete graph and is equal to
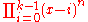
The windmill graph Wd(k,n) is proved not graceful
Graceful labeling
In graph theory, a graceful labeling of a graph with e edges is a labeling of its vertices with distinct integers between 0 and e inclusive, such that each edge is uniquely identified by the positive, or absolute difference between its endpoints. A graph which admits a graceful labeling is called a...
if k > 5. In 1979, Bermond has conjectured that Wd(4,n) is graceful for all n ≥ 4. This is known to be true for n ≤ 22. Bermond, Kotzig, and Turgeon proved that Wd(k,n) is not graceful when k = 4 and n = 2 or n = 3, and when k = 5 and m = 2. The windmill Wd(3,n) is graceful if and only if n ≡ 0 (mod 4) or n ≡ 1 (mod 4).

