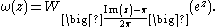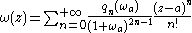In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the Wright omega function, denoted ω, is defined in terms of the Lambert W function as:

Uses

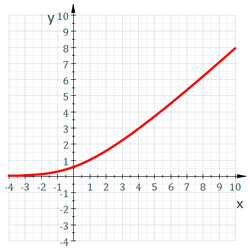
One of the main applications of this function is in the resolution of the equation z = ln(z), as the only solution is given by z = e^−ω(π i).

y = ω(z) is the unique solution, when for x ≤ −1, of the equation y + ln(y) = z. Except on those two rays, the Wright omega function is continuous

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

, even analytic

Analytic function

In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...

.

Properties

The Wright omega function satisfies the relation .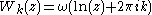

It also satisfies the differential equation

Differential equation

A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...

wherever ω is analytic (as can be seen by performing separation of variables

Separation of variables

In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....

 and recovering the equation 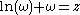), and as a consequence its integral

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

 can be expressed as:

Its Taylor series

Taylor series

In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....

 around the point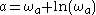 takes the form :

where

in which

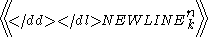
is a second-order Eulerian number

Eulerian number

In combinatorics the Eulerian number A, is the number of permutations of the numbers 1 to n in which exactly m elements are greater than the previous element...

.

Values

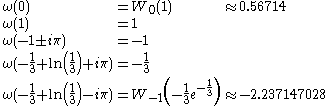
The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.