Yang–Mills existence and mass gap
Encyclopedia
In mathematics
, the Yang-Mills existence and mass gap problem is an unsolved problem
and one of the seven Millennium Prize Problems
defined by the Clay Mathematics Institute
which has offered a prize of US$1,000,000 to a person solving it.
The problem is phrased as follows:
In this statement, Yang–Mills theory is the (non-Abelian) quantum field theory
underlying the Standard Model
of particle physics
;
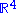is Euclidean 4-space
; the mass gap
Δ is the mass of the least massive particle predicted by the theory. Therefore, the winner must first prove that Yang–Mills theory exists and that it satisfies the standard of rigor that characterizes contemporary mathematical physics
, in particular constructive quantum field theory
, which is referenced in the papers 45 and 35 cited in the official problem description by Jaffe and Witten. The winner must then prove that the mass of the least massive particle of the force field predicted by the theory is strictly positive. For example, in the case of G=SU(3) - the strong nuclear interaction - the winner must prove that glueballs have a lower mass bound, and thus cannot be arbitrarily light.
with a cutoff scale. Since the beta-function
is positive for most models, it appears that most such models have a Landau pole
as it is not at all clear whether or not they have nontrivial UV fixed point
s. This means that if such a QFT
is well-defined at all scales, as it has to be to satisfy the axioms of axiomatic quantum field theory
, it would have to be trivial (i.e. a free field theory).
Quantum Yang-Mills theory with a non-abelian gauge group and no quarks is an exception, because asymptotic freedom
characterizes this theory, meaning that it has a trivial UV fixed point
. Hence it is the simplest nontrivial constructive QFT in 4 dimensions. (QCD
is a more complicated theory because it involves quark
s.)
It has already been well proven—at least at the level of rigor of theoretical physics
but not that of mathematical physics
—that the quantum Yang–Mills theory for a non-abelian Lie group
exhibits a property known as confinement. This property is covered in more detail in the relevant QCD articles (QCD
, color confinement, lattice gauge theory
, etc.), although not at the level of rigor of mathematical physics. A consequence of this property is that beyond a certain scale, known as the QCD scale (more properly, the confinement scale, as this theory is devoid of quarks), the color charges are connected by chromodynamic flux tubes
leading to a linear potential between the charges. Hence free color charge and free gluon
s cannot exist. In the absence of confinement, we would expect to see massless gluons, but since they are confined, all we see are color-neutral bound states of gluons, called glueball
s. If glueballs exist, they are massive, which is why we expect a mass gap.
Results from lattice gauge theory
have convinced many that quantum Yang–Mills theory for a non-abelian Lie group
model exhibits confinement—as indicated, for example, by an area law for the falloff of the vacuum expectation value (VEV)
of a Wilson loop
. However, these methods and results are not mathematically rigorous.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Yang-Mills existence and mass gap problem is an unsolved problem
Open problem
In science and mathematics, an open problem or an open question is a known problem that can be accurately stated, and has not yet been solved . Some questions remain unanswered for centuries before solutions are found...
and one of the seven Millennium Prize Problems
Millennium Prize Problems
The Millennium Prize Problems are seven problems in mathematics that were stated by the Clay Mathematics Institute in 2000. As of September 2011, six of the problems remain unsolved. A correct solution to any of the problems results in a US$1,000,000 prize being awarded by the institute...
defined by the Clay Mathematics Institute
Clay Mathematics Institute
The Clay Mathematics Institute is a private, non-profit foundation, based in Cambridge, Massachusetts. The Institute is dedicated to increasing and disseminating mathematical knowledge. It gives out various awards and sponsorships to promising mathematicians. The institute was founded in 1998...
which has offered a prize of US$1,000,000 to a person solving it.
The problem is phrased as follows:
- Yang–Mills Existence and Mass Gap. Prove that for any compact simple gauge group G, a non-trivial quantum Yang–Mills theory exists on
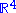and has a mass gap Δ > 0. Existence includes establishing axiomatic properties at least as strong as those cited in [45, 35].
In this statement, Yang–Mills theory is the (non-Abelian) quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
underlying the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
;
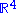is Euclidean 4-spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
; the mass gap
Mass gap
In quantum field theory, the mass gap is the difference in energy between the vacuum and the next lowest energy state. The energy of the vacuum is zero by definition, and assuming that all energy states can be thought of as particles in plane-waves, the mass gap is the mass of the lightest...
Δ is the mass of the least massive particle predicted by the theory. Therefore, the winner must first prove that Yang–Mills theory exists and that it satisfies the standard of rigor that characterizes contemporary mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, in particular constructive quantum field theory
Constructive quantum field theory
In mathematical physics, constructive quantum field theory is the field devoted to showing that quantum theory is mathematically compatible with special relativity. This demonstration requires new mathematics, in a sense analogous to Newton developing calculus in order to understand planetary...
, which is referenced in the papers 45 and 35 cited in the official problem description by Jaffe and Witten. The winner must then prove that the mass of the least massive particle of the force field predicted by the theory is strictly positive. For example, in the case of G=SU(3) - the strong nuclear interaction - the winner must prove that glueballs have a lower mass bound, and thus cannot be arbitrarily light.
Background
Most known and nontrivial (i.e. interacting) quantum field theories in 4 dimensions are effective field theoriesEffective field theory
In physics, an effective field theory is, as any effective theory, an approximate theory, that includes appropriate degrees of freedom to describe physical phenomena occurring at a chosen length scale, while ignoring substructure and degrees of freedom at shorter distances .-The renormalization...
with a cutoff scale. Since the beta-function
Beta-function
In theoretical physics, specifically quantum field theory, a beta function β encodes the dependence of a coupling parameter, g, on the energy scale, \mu of a given physical process....
is positive for most models, it appears that most such models have a Landau pole
Landau pole
In physics, the Landau pole is the momentum scale at which the coupling constant of a quantum field theory becomes infinite...
as it is not at all clear whether or not they have nontrivial UV fixed point
UV fixed point
In a quantum field theory, one may calculate an effectiveor running coupling constant that defines thecoupling of the theory measured at a given momentum scale.One example of such a coupling constantis the electric charge...
s. This means that if such a QFT
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
is well-defined at all scales, as it has to be to satisfy the axioms of axiomatic quantum field theory
Axiomatic quantum field theory
Axiomatic quantum field theory is a mathematical discipline which aims to describe quantum field theory in terms of rigorous axioms. It is strongly associated with functional analysis and operator algebras, but has also been studied in recent years from a more geometric and functorial...
, it would have to be trivial (i.e. a free field theory).
Quantum Yang-Mills theory with a non-abelian gauge group and no quarks is an exception, because asymptotic freedom
Asymptotic freedom
In physics, asymptotic freedom is a property of some gauge theories that causes interactions between particles to become arbitrarily weak at energy scales that become arbitrarily large, or, equivalently, at length scales that become arbitrarily small .Asymptotic freedom is a feature of quantum...
characterizes this theory, meaning that it has a trivial UV fixed point
UV fixed point
In a quantum field theory, one may calculate an effectiveor running coupling constant that defines thecoupling of the theory measured at a given momentum scale.One example of such a coupling constantis the electric charge...
. Hence it is the simplest nontrivial constructive QFT in 4 dimensions. (QCD
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
is a more complicated theory because it involves quark
Quark
A quark is an elementary particle and a fundamental constituent of matter. Quarks combine to form composite particles called hadrons, the most stable of which are protons and neutrons, the components of atomic nuclei. Due to a phenomenon known as color confinement, quarks are never directly...
s.)
It has already been well proven—at least at the level of rigor of theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
but not that of mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
—that the quantum Yang–Mills theory for a non-abelian Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
exhibits a property known as confinement. This property is covered in more detail in the relevant QCD articles (QCD
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
, color confinement, lattice gauge theory
Lattice gauge theory
In physics, lattice gauge theory is the study of gauge theories on a spacetime that has been discretized into a lattice. Gauge theories are important in particle physics, and include the prevailing theories of elementary particles: quantum electrodynamics, quantum chromodynamics and the Standard...
, etc.), although not at the level of rigor of mathematical physics. A consequence of this property is that beyond a certain scale, known as the QCD scale (more properly, the confinement scale, as this theory is devoid of quarks), the color charges are connected by chromodynamic flux tubes
QCD string
In quantum chromodynamics, , if a connection which is colour confining occurs, it is possible for stringlike degrees of freedom called QCD strings or QCD flux tubes to form...
leading to a linear potential between the charges. Hence free color charge and free gluon
Gluon
Gluons are elementary particles which act as the exchange particles for the color force between quarks, analogous to the exchange of photons in the electromagnetic force between two charged particles....
s cannot exist. In the absence of confinement, we would expect to see massless gluons, but since they are confined, all we see are color-neutral bound states of gluons, called glueball
Glueball
In particle physics, a glueball is a hypothetical composite particle. It consists solely of gluon particles, without valence quarks. Such a state is possible because gluons carry color charge and experience the strong interaction...
s. If glueballs exist, they are massive, which is why we expect a mass gap.
Results from lattice gauge theory
Lattice gauge theory
In physics, lattice gauge theory is the study of gauge theories on a spacetime that has been discretized into a lattice. Gauge theories are important in particle physics, and include the prevailing theories of elementary particles: quantum electrodynamics, quantum chromodynamics and the Standard...
have convinced many that quantum Yang–Mills theory for a non-abelian Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
model exhibits confinement—as indicated, for example, by an area law for the falloff of the vacuum expectation value (VEV)
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
of a Wilson loop
Wilson loop
In gauge theory, a Wilson loop is a gauge-invariant observable obtained from the holonomy of the gauge connection around a given loop...
. However, these methods and results are not mathematically rigorous.