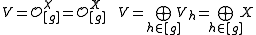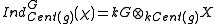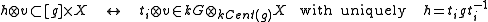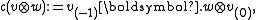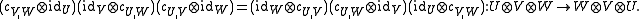Yetter-Drinfeld category
Encyclopedia
In mathematics
a Yetter–Drinfel'd category is a special type of braided monoidal category. It consists of modules over a Hopf algebra
which satisfy some additional axioms.
 denote the coproduct and S the antipode of H. Let V be a vector space
denote the coproduct and S the antipode of H. Let V be a vector space
over k. Then V is called a (left left) Yetter–Drinfel'd module over H if
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
a Yetter–Drinfel'd category is a special type of braided monoidal category. It consists of modules over a Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
which satisfy some additional axioms.
Definition
Let H be a Hopf algebra over a field k. Let denote the coproduct and S the antipode of H. Let V be a vector space
denote the coproduct and S the antipode of H. Let V be a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over k. Then V is called a (left left) Yetter–Drinfel'd module over H if
-
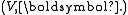 is a left H-moduleModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
is a left H-moduleModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, where denotes the left action of H on V and ⊗ denotes a tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
denotes the left action of H on V and ⊗ denotes a tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
, -
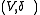 is a left H-comoduleComoduleIn mathematics, a comodule or corepresentation is a concept dual to a module. The definition of a comodule over a coalgebra is formed by dualizing the definition of a module over an associative algebra.-Formal definition:...
is a left H-comoduleComoduleIn mathematics, a comodule or corepresentation is a concept dual to a module. The definition of a comodule over a coalgebra is formed by dualizing the definition of a module over an associative algebra.-Formal definition:...
, where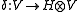 denotes the left coaction of H on V,
denotes the left coaction of H on V, - the maps
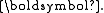 and
and  satisfy the compatibility condition
satisfy the compatibility condition
-
 for all
for all 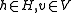 ,
,
- where, using Sweedler notationCoalgebraIn mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
, denotes the twofold coproduct of
denotes the twofold coproduct of 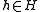 , and
, and 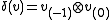 .
.
Examples
- Any left H-module over a cocommutative Hopf algebra H is a Yetter–Drinfel'd module with the trivial left coaction
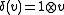 .
. - The trivial module
 with
with 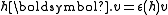 ,
, 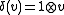 , is a Yetter–Drinfel'd module for all Hopf algebras H.
, is a Yetter–Drinfel'd module for all Hopf algebras H. - If H is the group algebraGroup ringIn algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
kG of an abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
G, then Yetter–Drinfel'd modules over H are precisely the G-graded G-modules. This means that
-
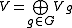 ,
,
- where each
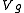 is a G-submodule of V.
is a G-submodule of V.
- More generally, if the group G is not abelian, then Yetter–Drinfel'd modules over H=kG are G-modules with a G-gradation
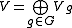 , such that
, such that 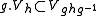 .
.
- Over the basfield
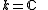 all finite-dimensional, irreducible/simple Yetter–Drinfel'd modules over a (nonabelian) group H=kG are uniquely given through a conjugacy classConjugacy classIn mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
all finite-dimensional, irreducible/simple Yetter–Drinfel'd modules over a (nonabelian) group H=kG are uniquely given through a conjugacy classConjugacy classIn mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
 together with
together with 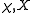 (character of) an irreducible group representation of the centralizerCentralizer and normalizerIn group theory, the centralizer and normalizer of a subset S of a group G are subgroups of G which have a restricted action on the elements of S and S as a whole, respectively...
(character of) an irreducible group representation of the centralizerCentralizer and normalizerIn group theory, the centralizer and normalizer of a subset S of a group G are subgroups of G which have a restricted action on the elements of S and S as a whole, respectively...
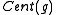 of some representing
of some representing  :
:
- As G-module take
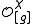 to be the induced moduleInduced representationIn mathematics, and in particular group representation theory, the induced representation is one of the major general operations for passing from a representation of a subgroup H to a representation of the group G itself. It was initially defined as a construction by Frobenius, for linear...
to be the induced moduleInduced representationIn mathematics, and in particular group representation theory, the induced representation is one of the major general operations for passing from a representation of a subgroup H to a representation of the group G itself. It was initially defined as a construction by Frobenius, for linear...
of :
:
-
- (this can be proven easily not to depend on the choice of g)
- To define the G-graduation (comodule) assign any element
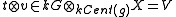 to the graduation layer:
to the graduation layer:
- It is very custom to directly construct
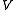 as direct sum of X´s and write down the G-action by choice of a specific set of representatives
as direct sum of X´s and write down the G-action by choice of a specific set of representatives 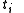 for the
for the 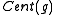 -cosetsCosetIn mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
-cosetsCosetIn mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
. From this approach, one often writes
-
- (this notation emphasizes the graduation
 , rather than the module structure)
, rather than the module structure)
- Over the basfield
Braiding
Let H be a Hopf algebra with invertible antipode S, and let V, W be Yetter–Drinfel'd modules over H. Then the map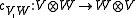 ,
,
-
- is invertible with inverse
- Further, for any three Yetter–Drinfel'd modules U, V, W the map c satisfies the braid relation
Yetter–Drinfel'd category
A monoidal categoryMonoidal categoryIn mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
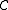 consisting of Yetter–Drinfel'd modules over a Hopf algebra H with bijective antipode is called a Yetter–Drinfel'd category. It is a braided monoidal category with the braiding c above. The category of Yetter–Drinfel'd modules over a Hopf algebra H with bijective antipode is denoted by
consisting of Yetter–Drinfel'd modules over a Hopf algebra H with bijective antipode is called a Yetter–Drinfel'd category. It is a braided monoidal category with the braiding c above. The category of Yetter–Drinfel'd modules over a Hopf algebra H with bijective antipode is denoted by 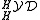 .
.
- Any left H-module over a cocommutative Hopf algebra H is a Yetter–Drinfel'd module with the trivial left coaction
- where, using Sweedler notation