Zakai equation
Encyclopedia
In filtering theory
the Zakai equation is a linear recursive filtering
equation for the un-normalized density of a hidden state. In contrast, the Kushner equation
gives a non-linear recursive equation for the normalized density of the hidden state. In principle either approach allows one to estimate a quantity (the state of a dynamical system) from noisy measurements, even when the system is non-linear (thus generalizing the earlier results of Wiener and Kalman for linear systems and solving a central problem in estimation theory
). The application of this approach to a specific engineering
situation may be problematic however, as these equations are quite complex. The Zakai equation is a bilinear stochastic partial differential equation
.
and a noisy measurement of the system state is available:
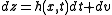
where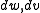
are independent Wiener process
es. Then the unnormalized conditional probability density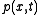
of the state at time t is given by the Zakai equation:
where the operator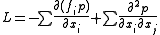
As previously mentioned p is an unnormalized density, i.e. it does not necessarily integrate to 1. After solving for p we can integrate it and normalize it if desired (an extra step not required in the Kushner approach).
Note that if the last two terms on the right hand side are omitted (by choosing h identically zero), we are left with a nonstochastic PDE: the familiar Kolmogorov Forward Equation, which describes the evolution of the state when no measurement information is available.
Filtering problem (stochastic processes)
In the theory of stochastic processes, the filtering problem is a mathematical model for a number of filtering problems in signal processing and the like. The general idea is to form some kind of "best estimate" for the true value of some system, given only some observations of that system...
the Zakai equation is a linear recursive filtering
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
equation for the un-normalized density of a hidden state. In contrast, the Kushner equation
Kushner equation
In filtering theory the Kushner equation is an equation for the conditional probability density of the state of a stochastic non-linear dynamical system, given noisy measurements of the state. It therefore provides the solution of the nonlinear filtering problem in estimation theory...
gives a non-linear recursive equation for the normalized density of the hidden state. In principle either approach allows one to estimate a quantity (the state of a dynamical system) from noisy measurements, even when the system is non-linear (thus generalizing the earlier results of Wiener and Kalman for linear systems and solving a central problem in estimation theory
Estimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
). The application of this approach to a specific engineering
Control engineering
Control engineering or Control systems engineering is the engineering discipline that applies control theory to design systems with predictable behaviors...
situation may be problematic however, as these equations are quite complex. The Zakai equation is a bilinear stochastic partial differential equation
Stochastic partial differential equation
Stochastic partial differential equations are similar to ordinary stochastic differential equations. They are essentially partial differential equations that have additional random terms. They can be exceedingly difficult to solve...
.
Overview
Assume the state of the system evolves according toand a noisy measurement of the system state is available:
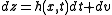
where
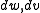are independent Wiener processWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
es. Then the unnormalized conditional probability density
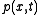of the state at time t is given by the Zakai equation:where the operator
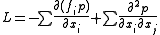
As previously mentioned p is an unnormalized density, i.e. it does not necessarily integrate to 1. After solving for p we can integrate it and normalize it if desired (an extra step not required in the Kushner approach).
Note that if the last two terms on the right hand side are omitted (by choosing h identically zero), we are left with a nonstochastic PDE: the familiar Kolmogorov Forward Equation, which describes the evolution of the state when no measurement information is available.