
Filtering problem (stochastic processes)
Encyclopedia
In the theory of stochastic processes, the filtering problem is a mathematical model for a number of filtering problems in signal processing
and the like. The general idea is to form some kind of "best estimate" for the true value of some system, given only some (potentially noisy) observations of that system. The problem of optimal non-linear filtering (even for the non-stationary case) was solved by Ruslan L. Stratonovich
(1959, 1960), see also Harold J. Kushner
's work and Moshe Zakai
's, who introduced a simplified dynamics for the unnormalized conditional law of the filter known as Zakai equation
. The solution, however, is infinite-dimensional in the general case. Certain approximations and special cases are well-understood: for example, the linear filters are optimal for Gaussian random variables, and are known as the Wiener filter
and the Kalman-Bucy filter. More generally, as the solution is infinite dimensional, it requires finite dimensional approximations to be implemented in a computer with finite memory. A finite dimensional approximated nonlinear filter may be more based on heuristics, such as the Extended Kalman Filter
or the Assumed Density Filters, or more methodologically oriented such as for example the Projection Filters, some sub-families of which are shown to coincide with the Assumed Density Filters.
In general, if the separation principle
applies, then filtering also arises as part of the solution of a optimal control
problem, i.e. the Kalman filter
is the estimation part of the optimal control solution to the Linear-quadratic-Gaussian control
problem.
(Ω, Σ, P) and suppose that the (random) state Yt in n-dimension
al Euclidean space
Rn of a system of interest at time t is a random variable
Yt : Ω → Rn given by the solution to an Itō
stochastic differential equation
of the form
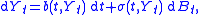
where B denotes standard p-dimensional Brownian motion
, b : [0, +∞) × Rn → Rn is the drift field, and σ : [0, +∞) × Rn → Rn×p is the diffusion field. It is assumed that observations Ht in Rm (note that m and n may, in general, be unequal) are taken for each time t according to
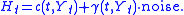
Adopting the Itō interpretation of the stochastic differential and setting
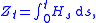
this gives the following stochastic integral representation for the observations Zt:
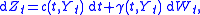
where W denotes standard r-dimensional Brownian motion
, independent of B and the initial condition X0, and c : [0, +∞) × Rn → Rn and γ : [0, +∞) × Rn → Rn×r satisfy
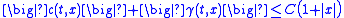
for all t and x and some constant C.
The filtering problem is the following: given observations Zs for 0 ≤ s ≤ t, what is the best estimate Ŷt of the true state Yt of the system based on those observations?
By "based on those observations" it is meant that Ŷt is measurable
with respect to the σ-algebra Gt generated by the observations Zs, 0 ≤ s ≤ t. Denote by K = K(Z, t) be collection of all Rn-valued random variables Y that are square-integrable and Gt-measurable:
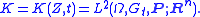
By "best estimate", it is meant that Ŷt minimizes the mean-square distance between Yt and all candidates in K:
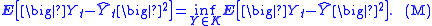
, and the general theory of Hilbert spaces implies that the solution Ŷt of the minimization problem (M) is given by
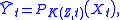
where PK(Z,t) denotes the orthogonal projection of L2(Ω, Σ, P; Rn) onto the linear subspace
K(Z, t) = L2(Ω, Gt, P; Rn). Furthermore, it is a general fact about conditional expectation
s that if F is any sub-σ-algebra of Σ then the orthogonal projection
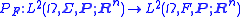
is exactly the conditional expectation operator E[·|F], i.e.,
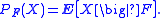
Hence,
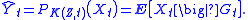
This elementary result is the basis for the general Fujisaki-Kallianpur-Kunita equation of filtering theory.
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
and the like. The general idea is to form some kind of "best estimate" for the true value of some system, given only some (potentially noisy) observations of that system. The problem of optimal non-linear filtering (even for the non-stationary case) was solved by Ruslan L. Stratonovich
Ruslan L. Stratonovich
Ruslan Leont'evich Stratonovich was an outstanding physicist, engineer, and probabilist. Professor Stratonovich was born on May 31, 1930 in Moscow, Russia...
(1959, 1960), see also Harold J. Kushner
Harold J. Kushner
Harold J. Kushner is an American applied mathematician and a Professor Emeritus of Applied Mathematics at Brown University. He is known for his work on the theory of stochastic stability , the theory of non-linear filtering , and for the development of numerical methods for stochastic control...
's work and Moshe Zakai
Moshe Zakai
Moshe Zakai is Distinguished Professor at the Technion, Israel in Electrical Engineering, member of the Israel Academy of Sciences and Humanities and Rothschild Prize winner.- Biography :...
's, who introduced a simplified dynamics for the unnormalized conditional law of the filter known as Zakai equation
Zakai equation
In filtering theory the Zakai equation is a linear recursive filtering equation for the un-normalized density of a hidden state. In contrast, the Kushner equation gives a non-linear recursive equation for the normalized density of the hidden state...
. The solution, however, is infinite-dimensional in the general case. Certain approximations and special cases are well-understood: for example, the linear filters are optimal for Gaussian random variables, and are known as the Wiener filter
Wiener filter
In signal processing, the Wiener filter is a filter proposed by Norbert Wiener during the 1940s and published in 1949. Its purpose is to reduce the amount of noise present in a signal by comparison with an estimation of the desired noiseless signal. The discrete-time equivalent of Wiener's work was...
and the Kalman-Bucy filter. More generally, as the solution is infinite dimensional, it requires finite dimensional approximations to be implemented in a computer with finite memory. A finite dimensional approximated nonlinear filter may be more based on heuristics, such as the Extended Kalman Filter
Extended Kalman filter
In estimation theory, the extended Kalman filter is the nonlinear version of the Kalman filter which linearizes about the current mean and covariance...
or the Assumed Density Filters, or more methodologically oriented such as for example the Projection Filters, some sub-families of which are shown to coincide with the Assumed Density Filters.
In general, if the separation principle
Separation principle
In control theory, a separation principle, more formally known as a principle of separation of estimation and control, states that under some assumptions the problem of designing an optimal feedback controller for a stochastic system can be solved by designing an optimal observer for the state of...
applies, then filtering also arises as part of the solution of a optimal control
Optimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
problem, i.e. the Kalman filter
Kalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
is the estimation part of the optimal control solution to the Linear-quadratic-Gaussian control
Linear-quadratic-Gaussian control
In control theory, the linear-quadratic-Gaussian control problem is one of the most fundamental optimal control problems. It concerns uncertain linear systems disturbed by additive white Gaussian noise, having incomplete state information and undergoing control subject to quadratic costs...
problem.
The mathematical formalism
Consider a probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
(Ω, Σ, P) and suppose that the (random) state Yt in n-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn of a system of interest at time t is a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
Yt : Ω → Rn given by the solution to an Itō
Kiyoshi Ito
was a Japanese mathematician whose work is now called Itō calculus. The basic concept of this calculus is the Itō integral, and among the most important results is Itō's lemma. The Itō calculus facilitates mathematical understanding of random events...
stochastic differential equation
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
of the form
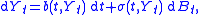
where B denotes standard p-dimensional Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
, b : [0, +∞) × Rn → Rn is the drift field, and σ : [0, +∞) × Rn → Rn×p is the diffusion field. It is assumed that observations Ht in Rm (note that m and n may, in general, be unequal) are taken for each time t according to
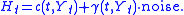
Adopting the Itō interpretation of the stochastic differential and setting
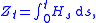
this gives the following stochastic integral representation for the observations Zt:
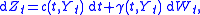
where W denotes standard r-dimensional Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
, independent of B and the initial condition X0, and c : [0, +∞) × Rn → Rn and γ : [0, +∞) × Rn → Rn×r satisfy
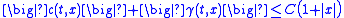
for all t and x and some constant C.
The filtering problem is the following: given observations Zs for 0 ≤ s ≤ t, what is the best estimate Ŷt of the true state Yt of the system based on those observations?
By "based on those observations" it is meant that Ŷt is measurable
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
with respect to the σ-algebra Gt generated by the observations Zs, 0 ≤ s ≤ t. Denote by K = K(Z, t) be collection of all Rn-valued random variables Y that are square-integrable and Gt-measurable:
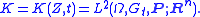
By "best estimate", it is meant that Ŷt minimizes the mean-square distance between Yt and all candidates in K:
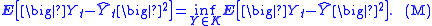
Basic result: orthogonal projection
The space K(Z, t) of candidates is a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, and the general theory of Hilbert spaces implies that the solution Ŷt of the minimization problem (M) is given by
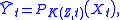
where PK(Z,t) denotes the orthogonal projection of L2(Ω, Σ, P; Rn) onto the linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
K(Z, t) = L2(Ω, Gt, P; Rn). Furthermore, it is a general fact about conditional expectation
Conditional expectation
In probability theory, a conditional expectation is the expected value of a real random variable with respect to a conditional probability distribution....
s that if F is any sub-σ-algebra of Σ then the orthogonal projection
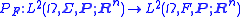
is exactly the conditional expectation operator E[·|F], i.e.,
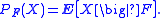
Hence,
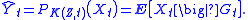
This elementary result is the basis for the general Fujisaki-Kallianpur-Kunita equation of filtering theory.

