
10-demicube
Encyclopedia
| Demidekeract (10-demicube) |
||
|---|---|---|
 Petrie polygon Petrie polygon In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets... projection |
||
| Type | Uniform 10-polytope 10-polytope In ten-dimensional geometry, a 10-polytope is a 10 dimensional polytope contained by 9-polytope facets. Each 8-polytope ridge being shared by exactly two 9-polytope facets.... |
|
| Family | demihypercube | |
| Coxeter symbol | 171 | |
| Schläfli symbol | {31,7,1} h{4,3,3,3,3,3,3,3,3} s{2,2,2,2,2,2,2,2,2} |
|
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
||
| 9-faces | 532 | 20 {31,6,1} Demienneract In geometry, a demienneract or 9-demicube is a uniform 9-polytope, constructed from the 9-cube, with alternated vertices deleted. It is part of a dimensionally infinite family of uniform polytopes called demihypercubes....  512 {38} |
| 8-faces | 5300 | 180 {31,5,1} Demiocteract In geometry, a demiocteract or 8-demicube is a uniform 8-polytope, constructed from the 8-hypercube, octeract, with alternated vertices deleted... 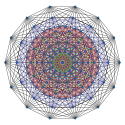 5120 {37} |
| 7-faces | 24000 | 960 {31,4,1} Demihepteract In geometry, a demihepteract or 7-demicube is a uniform 7-polytope, constructed from the 7-hypercube with alternated vertices deleted... 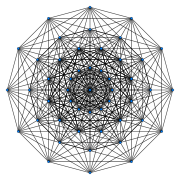 23040 {36} |
| 6-faces | 64800 | 3360 {31,3,1} Demihexeract In geometry, a 6-demicube or demihexteract is a uniform 6-polytope, constructed from a 6-cube with alternate vertices deleted. It is part of a dimensionally infinite family of uniform polytopes called demihypercubes.... 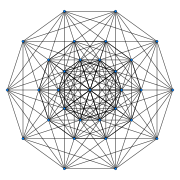 61440 {35} |
| 5-faces | 115584 | 8064 {31,2,1} Demipenteract In five dimensional geometry, a demipenteract or 5-demicube is a semiregular 5-polytope, constructed from a 5-hypercube with alternated vertices deleted.It was discovered by Thorold Gosset...  107520 {34} |
| 4-faces | 142464 | 13440 {31,1,1} 16-cell In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.... 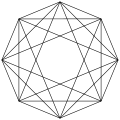 129024 {33} |
| Cells | 122880 | 15360 {31,0,1} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... 107520 {3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
| Faces | 61440 | {3} Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... |
| Edges | 11520 | |
| Vertices | 512 | |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
Rectified 9-simplex Rectified 9-simplex In nine-dimensional geometry, a rectified 9-simplex is a convex uniform 9-polytope, being a rectification of the regular 9-simplex.These polytopes are part of a family of 271 uniform 9-polytopes with A9 symmetry.... |
|
| Symmetry group Coxeter notation In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M... |
D10, [37,1,1] = [1+,4,38] [29]+ |
|
| Dual | ? | |
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... |
|
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a demidekeract or 10-demicube is a uniform 10-polytope
10-polytope
In ten-dimensional geometry, a 10-polytope is a 10 dimensional polytope contained by 9-polytope facets. Each 8-polytope ridge being shared by exactly two 9-polytope facets....
, constructed from the 10-cube
10-cube
In geometry, a 10-cube is a ten-dimensional hypercube. It has 1024 vertices, 5120 edges, 11520 square faces, 15360 cubic cells, 13440 tesseract 4-faces, 8064 5-cube 5-faces, 3360 6-cube 6-faces, 960 7-cube 7-faces, 180 8-cube 8-faces, and 20 9-cube 9-faces....
with alternated vertices deleted. It is part of a dimensionally infinite family of uniform polytope
Uniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
s called demihypercubes.
Coxeter named this polytope as 171 from its Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
, with a ring on
one of the 1-length Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
branches.
Cartesian coordinates
Cartesian coordinates for the vertices of a demidekeract centered at the origin are alternate halves of the dekeract:- (±1,±1,±1,±1,±1,±1,±1,±1,±1,±1)
with an odd number of plus signs.
Images
B10 coxeter plane |
D10 coxeter plane (Vertices are colored by multiplicity: red, orange, yellow, green = 1,2,4,8) |

