
A derivation of the discrete Fourier transform
Encyclopedia
In mathematics
, computer science
, and electrical engineering
, the discrete Fourier transform (DFT), occasionally called the finite Fourier transform
, is a transform for Fourier analysis of finite-domain discrete-time signals. As with most Fourier analysis, it expresses an input function in terms of a sum of sinusoidal components by determining the amplitude and phase of each component. Unlike the Fourier transform
, which operates upon continuous functions assumed to extend to infinity, the DFT operates upon discrete and finite sets of values: the input to the DFT is a finite sequence of real
or complex number
s, which makes the DFT ideal for processing information stored in computer
s. In particular, the DFT is widely employed in signal processing
and related fields to analyze the frequencies contained in a sampled signal, to solve partial differential equations, and to perform other operations such as convolution
s.
The article discrete Fourier transform
presents the definition of the transform, without derivation, as:
Here we take the view that the DFT is motivated by a desire to study continuous functions or waveforms and their continuous Fourier transforms using only a finite amount of data.
When the sequence {x[n]} represents a subset of the samples of a waveform x(t), we can model the process that created {x[n]} as applying a window function
to x(t), followed by sampling (or vice versa). It is instructive to envision how those operations affect our ability to observe the Fourier transform, X(ƒ). The window function widens every frequency component of X(ƒ) in a way that depends on the type of window used. That effect is called spectral leakage
. We can think of it as causing X(ƒ) to blur... thus a loss of resolution. The sampling operation causes the Fourier transform to become periodic. More precisely, what happens is that {x[n]} has no Fourier transform. It is undefined. But using the Poisson summation formula
a periodic function of continuous frequency can be constructed from the samples, and it comprises copies of the blurred X(ƒ) repeated at regular multiples of the sampling frequency (Fs = 1/T) and summed together where they overlap (called periodic summation):
The copies are aliases
of the original frequency components. In particular, due to the overlap, aliases can significantly distort the region containing the original X(ƒ) (if Fs is not sufficiently large enough to prevent it). But if the windowing and sampling are done with sufficient care, the Poisson summation still contains a reasonable semblance of X(ƒ). It is therefore a common practice to compute an arbitrary number of samples (N) of one cycle of the periodic function :
:
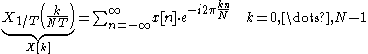
Since the kernel,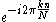 is N-periodic, it can readily be shown that this is equivalent to the following DFT
is N-periodic, it can readily be shown that this is equivalent to the following DFT
:
where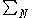 is a summation over any interval of length N, and
is a summation over any interval of length N, and 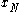 is another periodic summation:
is another periodic summation:
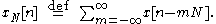
(the standard DFT) is just a simplification of when the x[n] sequence is zero outside the interval [0, N-1]. But regardless of the duration of the x[n] sequence, the inverse DFT produces the periodic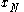 sequence. That is a consequence of substituting a discrete set of frequencies for the continuous
sequence. That is a consequence of substituting a discrete set of frequencies for the continuous  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, and electrical engineering
Electrical engineering
Electrical engineering is a field of engineering that generally deals with the study and application of electricity, electronics and electromagnetism. The field first became an identifiable occupation in the late nineteenth century after commercialization of the electric telegraph and electrical...
, the discrete Fourier transform (DFT), occasionally called the finite Fourier transform
Finite Fourier transform
In mathematics the finite Fourier transform may refer to either* another name for the discrete Fourier transformor* another name for the Fourier series coefficientsor...
, is a transform for Fourier analysis of finite-domain discrete-time signals. As with most Fourier analysis, it expresses an input function in terms of a sum of sinusoidal components by determining the amplitude and phase of each component. Unlike the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
, which operates upon continuous functions assumed to extend to infinity, the DFT operates upon discrete and finite sets of values: the input to the DFT is a finite sequence of real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, which makes the DFT ideal for processing information stored in computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
s. In particular, the DFT is widely employed in signal processing
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
and related fields to analyze the frequencies contained in a sampled signal, to solve partial differential equations, and to perform other operations such as convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
s.
The article discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
presents the definition of the transform, without derivation, as:
Here we take the view that the DFT is motivated by a desire to study continuous functions or waveforms and their continuous Fourier transforms using only a finite amount of data.
When the sequence {x[n]} represents a subset of the samples of a waveform x(t), we can model the process that created {x[n]} as applying a window function
Window function
In signal processing, a window function is a mathematical function that is zero-valued outside of some chosen interval. For instance, a function that is constant inside the interval and zero elsewhere is called a rectangular window, which describes the shape of its graphical representation...
to x(t), followed by sampling (or vice versa). It is instructive to envision how those operations affect our ability to observe the Fourier transform, X(ƒ). The window function widens every frequency component of X(ƒ) in a way that depends on the type of window used. That effect is called spectral leakage
Spectral leakage
Spectral leakage is an effect in the frequency analysis of finite-length signals or finite-length segments of infinite signals where it appears as if some energy has "leaked" out of the original signal spectrum into other frequencies....
. We can think of it as causing X(ƒ) to blur... thus a loss of resolution. The sampling operation causes the Fourier transform to become periodic. More precisely, what happens is that {x[n]} has no Fourier transform. It is undefined. But using the Poisson summation formula
Poisson summation formula
In mathematics, the Poisson summation formula is an equation that relates the Fourier series coefficients of the periodic summation of a function to values of the function's continuous Fourier transform. Consequently, the periodic summation of a function is completely defined by discrete samples...
a periodic function of continuous frequency can be constructed from the samples, and it comprises copies of the blurred X(ƒ) repeated at regular multiples of the sampling frequency (Fs = 1/T) and summed together where they overlap (called periodic summation):
The copies are aliases
Aliasing
In signal processing and related disciplines, aliasing refers to an effect that causes different signals to become indistinguishable when sampled...
of the original frequency components. In particular, due to the overlap, aliases can significantly distort the region containing the original X(ƒ) (if Fs is not sufficiently large enough to prevent it). But if the windowing and sampling are done with sufficient care, the Poisson summation still contains a reasonable semblance of X(ƒ). It is therefore a common practice to compute an arbitrary number of samples (N) of one cycle of the periodic function
 :
: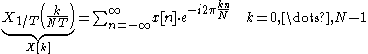
Since the kernel,
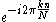 is N-periodic, it can readily be shown that this is equivalent to the following DFT
is N-periodic, it can readily be shown that this is equivalent to the following DFTDiscrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
:
where
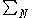 is a summation over any interval of length N, and
is a summation over any interval of length N, and 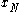 is another periodic summation:
is another periodic summation: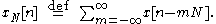
(the standard DFT) is just a simplification of when the x[n] sequence is zero outside the interval [0, N-1]. But regardless of the duration of the x[n] sequence, the inverse DFT produces the periodic
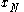 sequence. That is a consequence of substituting a discrete set of frequencies for the continuous
sequence. That is a consequence of substituting a discrete set of frequencies for the continuous  .
.

