
Acoustic theory
Encyclopedia
Acoustic theory is the field relating to mathematical description of sound
waves
. It is derived from fluid dynamics
. See acoustics
for the engineering
approach.
The propagation of sound waves in a fluid (such as water) can be modeled by an equation of motion (conservation of momentum
) and an equation of continuity (conservation of mass
). With some simplifications, in particular constant density, they can be given as follows:
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
waves
WAVES
The WAVES were a World War II-era division of the U.S. Navy that consisted entirely of women. The name of this group is an acronym for "Women Accepted for Volunteer Emergency Service" ; the word "emergency" implied that the acceptance of women was due to the unusual circumstances of the war and...
. It is derived from fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
. See acoustics
Acoustics
Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
for the engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
approach.
The propagation of sound waves in a fluid (such as water) can be modeled by an equation of motion (conservation of momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
) and an equation of continuity (conservation of mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
). With some simplifications, in particular constant density, they can be given as follows:
-
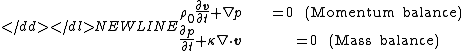
where is the acoustic pressure and
is the acoustic pressure and  is the acoustic fluid velocity vector,
is the acoustic fluid velocity vector, 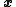 is the vector of spatial coordinates
is the vector of spatial coordinates 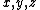 ,
,  is the time,
is the time,  is the static mass density of the medium and
is the static mass density of the medium and  is the bulk modulusBulk modulusThe bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
is the bulk modulusBulk modulusThe bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
of the medium. The bulk modulus can be expressed in terms of the density and the speed of sound in the medium (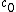 ) as
) as
The acoustic wave equationAcoustic wave equationIn physics, the acoustic wave equation governs the propagation of acoustic waves through a material medium. The form of the equation is a second order partial differential equation. The equation describes the evolution of acoustic pressure p or particle velocity u as a function of position r and...
is a combination of these two sets of balance equations and can be expressed as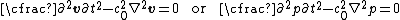
The acoustic wave equationAcoustic wave equationIn physics, the acoustic wave equation governs the propagation of acoustic waves through a material medium. The form of the equation is a second order partial differential equation. The equation describes the evolution of acoustic pressure p or particle velocity u as a function of position r and...
(and the mass and momentum balance equations) are often expressed in terms of a scalar potentialScalar potentialA scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
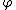 where
where  . In that case the acoustic wave equationAcoustic wave equationIn physics, the acoustic wave equation governs the propagation of acoustic waves through a material medium. The form of the equation is a second order partial differential equation. The equation describes the evolution of acoustic pressure p or particle velocity u as a function of position r and...
. In that case the acoustic wave equationAcoustic wave equationIn physics, the acoustic wave equation governs the propagation of acoustic waves through a material medium. The form of the equation is a second order partial differential equation. The equation describes the evolution of acoustic pressure p or particle velocity u as a function of position r and...
is written as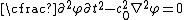
and the momentum balance and mass balance are expressed as
Derivation of the governing equations
The derivations of the above equations for waves in an acoustic medium are given below.
Conservation of momentum
The equations for the conservation of linear momentum for a fluid medium are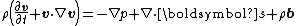
where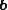 is the body force per unit mass,
is the body force per unit mass, 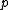 is the pressure, and
is the pressure, and 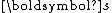 is the deviatoric stress. If
is the deviatoric stress. If  is the Cauchy stress, then
is the Cauchy stress, then
where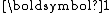 is the rank-2 identity tensor.
is the rank-2 identity tensor.
We make several assumptions to derive the momentum balance equation for an acoustic medium. These assumptions and the resulting forms of the momentum equations are outlined below.
Assumption 1: Newtonian fluid
In acoustics, the fluid medium is assumed to be NewtonianNewtonian fluidA Newtonian fluid is a fluid whose stress versus strain rate curve is linear and passes through the origin. The constant of proportionality is known as the viscosity.-Definition:...
. For a Newtonian fluid, the deviatoric stress tensor is related to the velocity by
where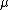 is the shear viscosityViscosityViscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
is the shear viscosityViscosityViscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
and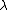 is the bulk viscosity.
is the bulk viscosity.
Therefore, the divergence of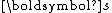 is given by
is given by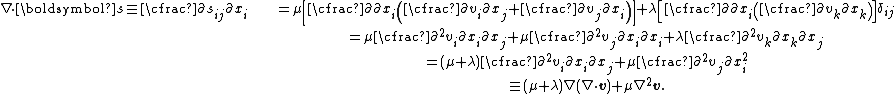
Using the identity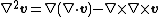 , we have
, we have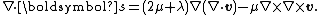
The equations for the conservation of momentum may then be written as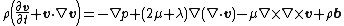
Assumption 2: Irrotational flow
For most acoustics problems we assume that the flow is irrotational, that is, the vorticity is zero. In that case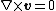
and the momentum equation reduces to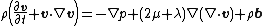
Assumption 3: No body forces
Another frequently made assumption is that effect of body forces on the fluid medium is negligible. The momentum equation then further simplifies to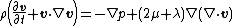
Assumption 4: No viscous forces
Additionally, if we assume that there are no viscous forces in the medium (the bulk and shear viscosities are zero), the momentum equation takes the form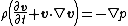
Assumption 5: Small disturbances
An important simplifying assumption for acoustic waves is that the amplitude of the disturbance of the field quantities is small. This assumption leads to the linear or small signal acoustic wave equation. Then we can express the variables as the sum of the (time averaged) mean field (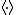 ) that varies in space and a small fluctuating field (
) that varies in space and a small fluctuating field ( ) that varies in space and time. That is
) that varies in space and time. That is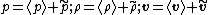
and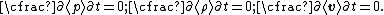
Then the momentum equation can be expressed as
Since the fluctuations are assumed to be small, products of the fluctuation terms can be neglected (to first order) and we have
Assumption 6: Homogeneous medium
Next we assume that the medium is homogeneous; in the sense that the time averaged variables
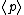 and
and 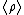 have zero gradients, i.e.,
have zero gradients, i.e.,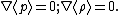
The momentum equation then becomes
Assumption 7: Medium at rest
At this stage we assume that the medium is at rest which implies that the mean velocity is zero, i.e. . Then the balance of momentum reduces to
. Then the balance of momentum reduces to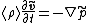
Dropping the tildes and using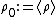 , we get the commonly used form of the acoustic momentum equation
, we get the commonly used form of the acoustic momentum equation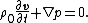
Conservation of mass
The equation for the conservation of mass in a fluid volume (without any mass sources or sinks) is given by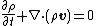
where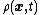 is the mass density of the fluid and
is the mass density of the fluid and  is the fluid velocity.
is the fluid velocity.
The equation for the conservation of mass for an acoustic medium can also be derived in a manner similar to that used for the conservation of momentum.
Assumption 1: Small disturbances
From the assumption of small disturbances we have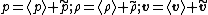
and
Then the mass balance equation can be written as
If we neglect higher than first order terms in the fluctuations, the mass balance equation becomes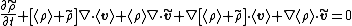
Assumption 2: Homogeneous medium
Next we assume that the medium is homogeneous, i.e.,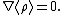
Then the mass balance equation takes the form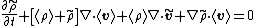
Assumption 3: Medium at rest
At this stage we assume that the medium is at rest, i.e.,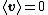 . Then the mass balance equation can be expressed as
. Then the mass balance equation can be expressed as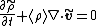
Assumption 4: Ideal gas, adiabatic, reversible
In order to close the system of equations we need an equation of stateEquation of stateIn physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...
for the pressure. To do that we assume that the medium is an ideal gasIdeal gasAn ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
and all acoustic waves compress the medium in an adiabatic and reversible manner. The equation of state can then be expressed in the form of the differential equation:
where is the specific heat at constant pressure,
is the specific heat at constant pressure, 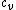 is the specific heat at constant volume, and
is the specific heat at constant volume, and  is the wave speed. The value of
is the wave speed. The value of 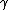 is 1.4 if the acoustic medium is air.
is 1.4 if the acoustic medium is air.
For small disturbances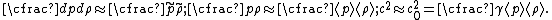
where is the speed of soundSpeed of soundThe speed of sound is the distance travelled during a unit of time by a sound wave propagating through an elastic medium. In dry air at , the speed of sound is . This is , or about one kilometer in three seconds or approximately one mile in five seconds....
is the speed of soundSpeed of soundThe speed of sound is the distance travelled during a unit of time by a sound wave propagating through an elastic medium. In dry air at , the speed of sound is . This is , or about one kilometer in three seconds or approximately one mile in five seconds....
in the medium.
Therefore,
The balance of mass can then be written as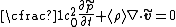
Dropping the tildes and defining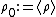 gives us the commonly used expression for the balance of mass in an acoustic medium:
gives us the commonly used expression for the balance of mass in an acoustic medium: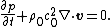
Governing equations in cylindrical coordinates
If we use a cylindrical coordinate systemCylindrical coordinate systemA cylindrical coordinate system is a three-dimensional coordinate systemthat specifies point positions by the distance from a chosen reference axis, the direction from the axis relative to a chosen reference direction, and the distance from a chosen reference plane perpendicular to the axis...
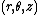 with basis vectors
with basis vectors 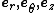 , then the gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
, then the gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of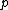 and the divergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
and the divergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of are given by
are given by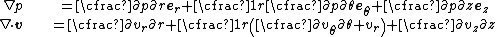
where the velocityVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
has been expressed as .
.
The equations for the conservation of momentum may then be written as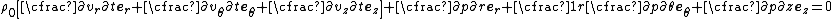
In terms of components, these three equations for the conservation of momentum in cylindrical coordinates are
The equation for the conservation of massConservation of massThe law of conservation of mass, also known as the principle of mass/matter conservation, states that the mass of an isolated system will remain constant over time...
can similarly be written in cylindrical coordinates as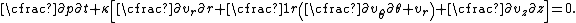
Time harmonic acoustic equations in cylindrical coordinates
The acoustic equations for the conservation of momentum and the conservation of massConservation of massThe law of conservation of mass, also known as the principle of mass/matter conservation, states that the mass of an isolated system will remain constant over time...
are often expressed in time harmonicHarmonicA harmonic of a wave is a component frequency of the signal that is an integer multiple of the fundamental frequency, i.e. if the fundamental frequency is f, the harmonics have frequencies 2f, 3f, 4f, . . . etc. The harmonics have the property that they are all periodic at the fundamental...
form (at fixed frequencyFrequencyFrequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
). In that case, the pressures and the velocity are assumed to be time harmonic functions of the form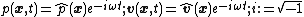
where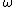 is the frequency. Substitution of these expressions into the governing equations in cylindrical coordinates gives us the fixed frequency form of the conservation of momentum
is the frequency. Substitution of these expressions into the governing equations in cylindrical coordinates gives us the fixed frequency form of the conservation of momentum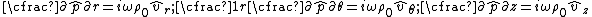
and the fixed frequency form of the conservation of massConservation of massThe law of conservation of mass, also known as the principle of mass/matter conservation, states that the mass of an isolated system will remain constant over time...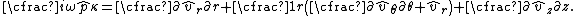
Special case: No z-dependence
In the special case where the field quantities are independent of the z-coordinate we can eliminate to get
to get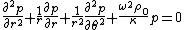
Assuming that the solution of this equation can be written as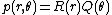
we can write the partial differential equation as
The left hand side is not a function of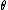 while the right hand side is not a function of
while the right hand side is not a function of  . Hence,
. Hence,
where is a constant. Using the substitution
is a constant. Using the substitution
we have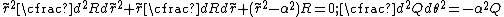
The equation on the left is the Bessel equation which has the general solution
where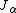 is the cylindrical Bessel functionBessel functionIn mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
is the cylindrical Bessel functionBessel functionIn mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
of the first kind and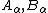 are undetermined constants. The equation on the right has the general solution
are undetermined constants. The equation on the right has the general solution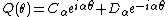
where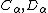 are undetermined constants. Then the solution of the acoustic wave equation is
are undetermined constants. Then the solution of the acoustic wave equation is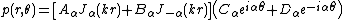
Boundary conditions are needed at this stage to determine and the other undetermined constants.
and the other undetermined constants.
See also
- AeroacousticsAeroacousticsAeroacoustics is a branch of acoustics that studies noise generation via either turbulent fluid motion or aerodynamic forces interacting with surfaces. Noise generation can also be associated with periodically varying flows...
- Transfer functionTransfer functionA transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
- SoundSoundSound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
- Acoustic impedanceAcoustic impedanceThe acoustic impedance at a particular frequency indicates how much sound pressure is generated by a given air vibration at that frequency. The acoustic impedance Z is frequency dependent and is very useful, for example, for describing the behaviour of musical wind instruments...
- Acoustic resistance
- law of gasesGas lawsThe early gas laws were developed at the end of the 18th century, when scientists began to realize that relationships between the pressure, volume and temperature of a sample of gas could be obtained which would hold for all gases...
- FrequencyFrequencyFrequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
- Fourier analysis
- Music theoryMusic theoryMusic theory is the study of how music works. It examines the language and notation of music. It seeks to identify patterns and structures in composers' techniques across or within genres, styles, or historical periods...
- Voice production
- FormantFormantFormants are defined by Gunnar Fant as 'the spectral peaks of the sound spectrum |P|' of the voice. In speech science and phonetics, formant is also used to mean an acoustic resonance of the human vocal tract...
- Speech synthesisSpeech synthesisSpeech synthesis is the artificial production of human speech. A computer system used for this purpose is called a speech synthesizer, and can be implemented in software or hardware...
- Loudspeaker acousticsLoudspeaker acousticsLoudspeaker acoustics is a subfield of acoustical engineering concerned with the reproduction of sound and the parameters involved in doing so in actual equipment....
- Lumped component model
-


