
Affine geometry of curves
Encyclopedia
In the mathematical
field of differential geometry, the affine geometry of curves is the study of curve
s in an affine space
, and specifically the properties of such curves which are invariant
under the special affine group
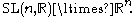
In the classical Euclidean geometry of curves, the fundamental tool is the Frenet–Serret frame. In affine geometry, the Frenet–Serret frame is no longer well-defined, but it is possible to define another canonical moving frame
along a curve which plays a similar decisive role. The theory was developed in the early 20th century, largely from the efforts of Wilhelm Blaschke
and Jean Favard
.

Such a curve is said to be parametrized by its affine arclength. For such a parameterization,
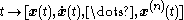
determines a mapping into the special affine group, known as a special affine frame for the curve. That is, at each point of the, the quantities define a special affine frame
define a special affine frame
for the affine space Rn, consisting of a point x of the space and a special linear basis attached to the point at x. The pullback of the Maurer–Cartan form along this map gives a complete set of affine structural invariants of the curve. In the plane, this gives a single scalar invariant, the affine curvature
attached to the point at x. The pullback of the Maurer–Cartan form along this map gives a complete set of affine structural invariants of the curve. In the plane, this gives a single scalar invariant, the affine curvature
of the curve.
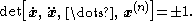
If n≡0 (mod 4) or n≡3 (mod 4) then the sign of this determinant is a discrete invariant of the curve. A curve is called dextrorse (right winding, frequently weinwendig in German) if it is +1, and sinistrorse (left winding, frequently hopfenwendig in German) if it is −1.
In three-dimensions, a right-handed helix
is dextrorse, and a left-handed helix is sinistrorse.
s, k1, …, kn−1 of x are defined by
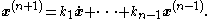
That such an expression is possible follows by computing the derivative of the determinant
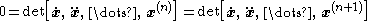
so that x(n+1) is a linear combination of x′, …, x(n−1).
Consider the matrix

whose columns are the first n derivatives of x (still parameterized by special affine arclength). Then,
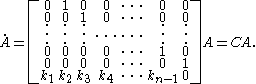
In concrete terms, the matrix C is the pullback of the Maurer–Cartan form of the special linear group along the frame given by the first n derivatives of x.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of differential geometry, the affine geometry of curves is the study of curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s in an affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
, and specifically the properties of such curves which are invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
under the special affine group
Special affine group
In the mathematical study of transformation groups, the special affine group is the group of affine transformations of a fixed affine space which preserve volume...
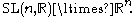
In the classical Euclidean geometry of curves, the fundamental tool is the Frenet–Serret frame. In affine geometry, the Frenet–Serret frame is no longer well-defined, but it is possible to define another canonical moving frame
Moving frame
In mathematics, a moving frame is a flexible generalization of the notion of an ordered basis of a vector space often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space.-Introduction:...
along a curve which plays a similar decisive role. The theory was developed in the early 20th century, largely from the efforts of Wilhelm Blaschke
Wilhelm Blaschke
Wilhelm Johann Eugen Blaschke was an Austro-Hungarian differential and integral geometer.His students included Shiing-Shen Chern, Luis Santaló, and Emanuel Sperner....
and Jean Favard
Jean Favard
Jean Favard was a French mathematician who worked on analysis.During World War II he was a prisoner of war in Germany.He also was a President of the French Mathematical Society in 1946....
.
The affine frame
Let x(t) be a curve in Rn. Assume, as one does in the Euclidean case, that the first n derivatives of x(t) are linearly independent so that, in particular, x(t) does not lie in any lower-dimensional affine subspace of Rn. Then the curve parameter t can be normalized by setting determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

Such a curve is said to be parametrized by its affine arclength. For such a parameterization,
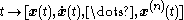
determines a mapping into the special affine group, known as a special affine frame for the curve. That is, at each point of the, the quantities
 define a special affine frame
define a special affine frameAffine frame
In affine geometry, a branch of mathematics, an affine frame in an affine space A consists of a choice P of origin of A along with a basis of the space of vectors based at P....
for the affine space Rn, consisting of a point x of the space and a special linear basis
 attached to the point at x. The pullback of the Maurer–Cartan form along this map gives a complete set of affine structural invariants of the curve. In the plane, this gives a single scalar invariant, the affine curvature
attached to the point at x. The pullback of the Maurer–Cartan form along this map gives a complete set of affine structural invariants of the curve. In the plane, this gives a single scalar invariant, the affine curvatureAffine curvature
Special affine curvature, also known as the equi-affine curvature or affine curvature, is a particular type of curvature that is defined on a plane curve that remains unchanged under a special affine transformation . The curves of constant equi-affine curvature k are precisely all non-singular...
of the curve.
Discrete invariant
The normalization of the curve parameter s was selected above so that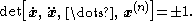
If n≡0 (mod 4) or n≡3 (mod 4) then the sign of this determinant is a discrete invariant of the curve. A curve is called dextrorse (right winding, frequently weinwendig in German) if it is +1, and sinistrorse (left winding, frequently hopfenwendig in German) if it is −1.
In three-dimensions, a right-handed helix
Helix
A helix is a type of smooth space curve, i.e. a curve in three-dimensional space. It has the property that the tangent line at any point makes a constant angle with a fixed line called the axis. Examples of helixes are coil springs and the handrails of spiral staircases. A "filled-in" helix – for...
is dextrorse, and a left-handed helix is sinistrorse.
Curvature
Suppose that the curve x in Rn is parameterized by affine arclength. Then the affine curvatureAffine curvature
Special affine curvature, also known as the equi-affine curvature or affine curvature, is a particular type of curvature that is defined on a plane curve that remains unchanged under a special affine transformation . The curves of constant equi-affine curvature k are precisely all non-singular...
s, k1, …, kn−1 of x are defined by
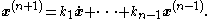
That such an expression is possible follows by computing the derivative of the determinant
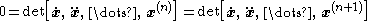
so that x(n+1) is a linear combination of x′, …, x(n−1).
Consider the matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

whose columns are the first n derivatives of x (still parameterized by special affine arclength). Then,
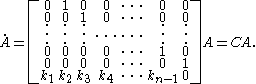
In concrete terms, the matrix C is the pullback of the Maurer–Cartan form of the special linear group along the frame given by the first n derivatives of x.

