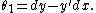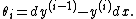Affine curvature
Encyclopedia
Special affine curvature, also known as the equi-affine curvature or affine curvature, is a particular type of curvature
that is defined on a plane curve
that remains unchanged under a special affine transformation
(an affine transformation
that preserves area
). The curves of constant equi-affine curvature k are precisely all non-singular plane conics
. Those with k > 0 are ellipse
s, those with k = 0 are parabola
s, and those with k < 0 are hyperbola
s.
The usual Euclidean curvature of a curve at a point is the curvature of its osculating circle
, the unique circle making second order contact (having three point contact) with the curve at the point. In the same way,
the special affine curvature of a curve at a point P is the special affine curvature of its hyperosculating conic, which is the unique conic making fourth order contact
(having five point contact) with the curve at P. In other words it is the
limiting position of the (unique) conic through P and four points P1, P2, P3, P4 on the curve, as each of the points approaches P:
In some contexts, the affine curvature refers to a differential invariant κ of the general affine group
, which may readily obtained from the special affine curvature k by κ = k−3/2dk/ds, where s is the special affine arc length. Where the general affine group is not used, the special affine curvature k is sometimes also called the affine curvature .
. Choose co-ordinates for the affine plane such that the area of the parallelogram spanned by two vectors 
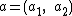and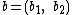 
is given by the determinant
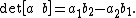
In particular, the determinant
is a well-defined invariant of the special affine group, and gives the signed area of the parallelogram spanned by the velocity and acceleration of the curve β. Consider a reparameterization of the curve β, say with a new parameter s related to t by means of a regular reparameterization s = s(t). This determinant undergoes then a transformation of the following sort, by the chain rule
:
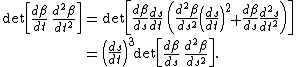
The reparameterization can be chosen so that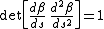
provided the velocity and acceleration, dβ/dt and d2β/dt2 are linearly independent. Existence and uniqueness of such a parameterization follows by integration:
This integral is called the special affine arclength, and a curve carrying this parameterization is said to be parameterized with respect to its special affine arclength.
Here β′ denotes the derivative of β with respect to s.
More generally , for a plane curve with arbitrary parameterization
the special affine curvature is:
provided the first and second derivatives of the curve are linearly independent. In the special case of a graph y = y(x), these formulas reduce to
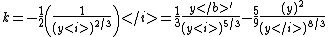
where the prime denotes differentiation with respect to x .
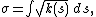
sometimes called the affine arclength (although this risks confusion with the special affine arclength described above). The second is referred to as the affine curvature:
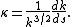
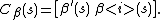
Note that det Cβ, since β is assumed to carry the special affine arclength parameterization, and that
It follows from the form of Cβ that
By applying a suitable special affine transformation, we can arrange that Cβ(0) = I is the identity matrix. Since k is constant, it follows that Cβ is given by the matrix exponential
The three cases are now as follows.
k = 0
If the curvature vanishes identically, then upon passing to a limit,
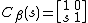
so β'(s) = (1,s), and so integration gives
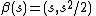
up to an overall constant translation, which is the special affine parameterization of the parabola y = x2/2.
k > 0
If the special affine curvature is positive, then it follows that
so that
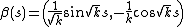
up to a translation, which is the special affine parameterization of the ellipse kx2 + k2y2 = 1.
k < 0
If k is negative, then the trigonometric functions in Cβ give way to hyperbolic function
s:
Thus
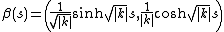
up to a translation, which is the special affine parameterization of the hyperbola
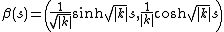
In fact, a slightly stronger statement holds:
This is analogous to the fundamental theorem of curves in the classical Euclidean differential geometry of curves
, in which the complete classification of plane curves up to Euclidean motion depends on a single function κ, the curvature of the curve. It follows essentially by applying the Picard–Lindelöf theorem to the system
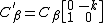
where Cβ = [β′ β′′]. An alternative approach, rooted in the theory of moving frame
s, is to apply the existence of a primitive for the Darboux derivative
.
. For simplicity, suppose that an affine plane curve is given in the form of a graph y = y(x). The special affine group acts on the Cartesian plane via transformations of the form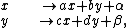
with ad − bc = 1. The following vector field
s span the Lie algebra
of infinitesimal generators of the special affine group:
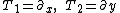
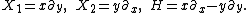
An affine transformation not only acts on points, but also on the tangent lines to graphs of the form y = y(x). That is, there is an action of the special affine group on triples of coordinates
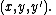
The group action is generated by vector fields
defined on the space of three variables (x,y,y′). These vector fields can be determined by the following two requirements: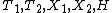
, respectively.
The vectors must preserve up to scale the contact structure of the jet space
where L is the Lie derivative
.
Similarly, the action of the group can be extended to the space of any number of derivatives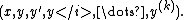
The prolonged vector fields generating the action of the special affine group must then inductively satisfy, for each generator X ∈ {T1,T2,X1,X2,H}:
Carrying out the inductive construction up to order 4 gives
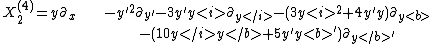
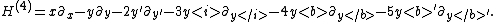
The special affine curvature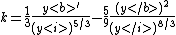
does not depend explicitly on x, y, or y′, and so satisfies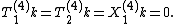
The vector field H acts diagonally as a modified homogeneity operator, and it is readily verified that H(4)k = 0. Finally,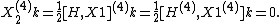
The five vector fields
form an involutive distribution on (an open subset of) R6 so that, by the Frobenius integration theorem, they integrate locally to give a foliation of R6 by five-dimensional leaves. Concretely, each leaf is a local orbit of the special affine group. The function k parameterizes these leaves.
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
that is defined on a plane curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
that remains unchanged under a special affine transformation
Special affine group
In the mathematical study of transformation groups, the special affine group is the group of affine transformations of a fixed affine space which preserve volume...
(an affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
that preserves area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
). The curves of constant equi-affine curvature k are precisely all non-singular plane conics
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
. Those with k > 0 are ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
s, those with k = 0 are parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
s, and those with k < 0 are hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
s.
The usual Euclidean curvature of a curve at a point is the curvature of its osculating circle
Osculating circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point p on the curve has been traditionally defined as the circle passing through p and a pair of additional points on the curve infinitesimally close to p...
, the unique circle making second order contact (having three point contact) with the curve at the point. In the same way,
the special affine curvature of a curve at a point P is the special affine curvature of its hyperosculating conic, which is the unique conic making fourth order contact
Contact (mathematics)
In mathematics, contact of order k of functions is an equivalence relation, corresponding to having the same value at a point P and also the same derivatives there, up to order k. The equivalence classes are generally called jets...
(having five point contact) with the curve at P. In other words it is the
limiting position of the (unique) conic through P and four points P1, P2, P3, P4 on the curve, as each of the points approaches P:
In some contexts, the affine curvature refers to a differential invariant κ of the general affine group
Affine group
In mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.It is a Lie group if K is the real or complex field or quaternions....
, which may readily obtained from the special affine curvature k by κ = k−3/2dk/ds, where s is the special affine arc length. Where the general affine group is not used, the special affine curvature k is sometimes also called the affine curvature .
Special affine arclength
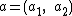To define the special affine curvature, it is necessary first to define the special affine arclength (also called the equi-affine arclength). Consider an affine plane curve. Choose co-ordinates for the affine plane such that the area of the parallelogram spanned by two vectors and 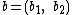is given by the determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
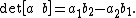
In particular, the determinant
is a well-defined invariant of the special affine group, and gives the signed area of the parallelogram spanned by the velocity and acceleration of the curve β. Consider a reparameterization of the curve β, say with a new parameter s related to t by means of a regular reparameterization s = s(t). This determinant undergoes then a transformation of the following sort, by the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
:
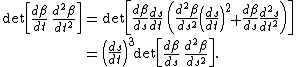
The reparameterization can be chosen so that
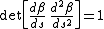
provided the velocity and acceleration, dβ/dt and d2β/dt2 are linearly independent. Existence and uniqueness of such a parameterization follows by integration:
This integral is called the special affine arclength, and a curve carrying this parameterization is said to be parameterized with respect to its special affine arclength.
Special affine curvature
Suppose that β(s) is a curve parameterized with its special affine arclength. Then the special affine curvature (or equi-affine curvature) is given byHere β′ denotes the derivative of β with respect to s.
More generally , for a plane curve with arbitrary parameterization
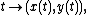
the special affine curvature is:
provided the first and second derivatives of the curve are linearly independent. In the special case of a graph y = y(x), these formulas reduce to
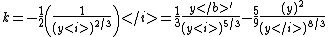
where the prime denotes differentiation with respect to x .
Affine curvature
Suppose as above that β(s) is a curve parameterized by special affine arclength. There are a pair of invariants of the curve that are invariant under the full general affine group — the group of all affine motions of the plane, not just those that are area-preserving. The first of these is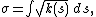sometimes called the affine arclength (although this risks confusion with the special affine arclength described above). The second is referred to as the affine curvature:
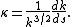
Conics
Suppose that β(s) is a curve parameterized by special affine arclength with constant affine curvature k. Let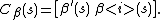Note that det Cβ, since β is assumed to carry the special affine arclength parameterization, and that
It follows from the form of Cβ that
By applying a suitable special affine transformation, we can arrange that Cβ(0) = I is the identity matrix. Since k is constant, it follows that Cβ is given by the matrix exponential
Matrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
The three cases are now as follows.
k = 0
If the curvature vanishes identically, then upon passing to a limit,
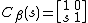
so β'(s) = (1,s), and so integration gives
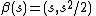
up to an overall constant translation, which is the special affine parameterization of the parabola y = x2/2.
k > 0
If the special affine curvature is positive, then it follows that
so that
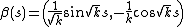
up to a translation, which is the special affine parameterization of the ellipse kx2 + k2y2 = 1.
k < 0
If k is negative, then the trigonometric functions in Cβ give way to hyperbolic function
Hyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
s:
Thus
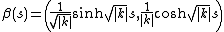
up to a translation, which is the special affine parameterization of the hyperbola
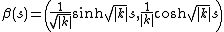
Characterization up to affine congruence
The special affine curvature of an immersed curve is the only (local) invariant of the curve in the following sense:- If two curves have the same special affine curvature at every point, then one curve is obtained from the other by means of a special affine transformation.
In fact, a slightly stronger statement holds:
- Given any continuous function k : [a,b] → R, there exists a curve β whose first and second derivatives are linearly independent, such that the special affine curvature of β relative to the special affine parameterization is equal to the given function k. The curve β is uniquely determined up to a special affine transformation.
This is analogous to the fundamental theorem of curves in the classical Euclidean differential geometry of curves
Differential geometry of curves
Differential geometry of curves is the branch of geometry that dealswith smooth curves in the plane and in the Euclidean space by methods of differential and integral calculus....
, in which the complete classification of plane curves up to Euclidean motion depends on a single function κ, the curvature of the curve. It follows essentially by applying the Picard–Lindelöf theorem to the system
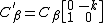
where Cβ = [β′ β′′]. An alternative approach, rooted in the theory of moving frame
Moving frame
In mathematics, a moving frame is a flexible generalization of the notion of an ordered basis of a vector space often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space.-Introduction:...
s, is to apply the existence of a primitive for the Darboux derivative
Darboux derivative
The Darboux derivative of a map between a manifold and a Lie group is a variant of the standard derivative. In a certain sense, it is arguably a more natural generalization of the single-variable derivative...
.
Derivation of the curvature by affine invariance
The special affine curvature can be derived explicitly by techniques of invariant theoryInvariant theory
Invariant theory is a branch of abstract algebra dealing with actions of groups on algebraic varieties from the point of view of their effect on functions...
. For simplicity, suppose that an affine plane curve is given in the form of a graph y = y(x). The special affine group acts on the Cartesian plane via transformations of the form
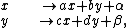
with ad − bc = 1. The following vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s span the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of infinitesimal generators of the special affine group:
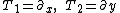
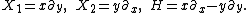
An affine transformation not only acts on points, but also on the tangent lines to graphs of the form y = y(x). That is, there is an action of the special affine group on triples of coordinates
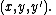
The group action is generated by vector fields
defined on the space of three variables (x,y,y′). These vector fields can be determined by the following two requirements:
- Under the projection onto the
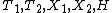, respectively.
Jet (mathematics)
In mathematics, the jet is an operation which takes a differentiable function f and produces a polynomial, the truncated Taylor polynomial of f, at each point of its domain...
-
- Concretely, this means that the generators
Lie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
.
Similarly, the action of the group can be extended to the space of any number of derivatives
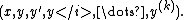
The prolonged vector fields generating the action of the special affine group must then inductively satisfy, for each generator X ∈ {T1,T2,X1,X2,H}:
- The projection of X(k) onto the space of variables (x,y,y′,…,y(k−1)) is X(k−1).
- X(k) preserves the contact ideal:
-
- where
Carrying out the inductive construction up to order 4 gives
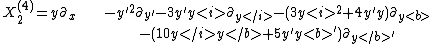
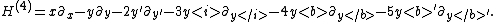
The special affine curvature
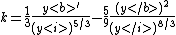
does not depend explicitly on x, y, or y′, and so satisfies
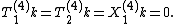
The vector field H acts diagonally as a modified homogeneity operator, and it is readily verified that H(4)k = 0. Finally,
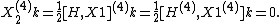
The five vector fields
form an involutive distribution on (an open subset of) R6 so that, by the Frobenius integration theorem, they integrate locally to give a foliation of R6 by five-dimensional leaves. Concretely, each leaf is a local orbit of the special affine group. The function k parameterizes these leaves.