Alexandroff extension
Encyclopedia
In mathematical
field of topology
, the Alexandroff extension is a way to extend a noncompact topological space
by adjoining a single point in such a way that the resulting space is compact
. It is named for the Russian mathematician Pavel Alexandrov.
More precisely, let X be a topological space. Then the Alexandroff extension of X is a certain compact space X* together with an open embedding c : X → X* such that the complement of X in X* consists of a single point, typically denoted ∞. The map c is a Hausdorff compactification
if and only if X is a locally compact, noncompact Hausdorff space
. For such spaces the Alexandroff extension is called the one-point compactification or Alexandroff compactification. The advantages of the Alexandroff compactification lie in its simple, often geometrically meaningful structure and the fact that it is in a precise sense minimal among all compactifications; the disadvantage lies in the fact that it only gives a Hausdorff compactification on the class of locally compact, noncompact Hausdorff spaces, unlike the Stone–Čech compactification
which exists for any Tychonoff space
, a much larger class of spaces.
. Recall that the stereographic projection S gives an explicit homeomorphism from the unit sphere minus the north pole (0,0,1) to the Euclidean plane. Therefore the inverse stereographic projection
is an open, dense embedding into a compact Hausdorff space obtained by adjoining the additional point 
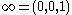. Under the stereographic projection latitudinal circles 
get mapped to planar circles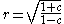 
. It follows that the deleted neighborhood basis of 
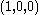given by the punctured spherical caps 
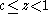corresponds to the complements of closed planar disks 
. More qualitatively, a neighborhood basis at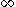 
is furnished by the sets 
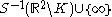as K ranges through the compact subsets of 
. This example already contains the key concepts of the general case.
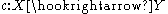be an embedding from a topological space X to a compact Hausdorff topological space Y, with dense image and one-point remainder 
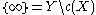. Then c(X) is open in a compact Hausdorff space so is locally compact Hausdorff, hence its homeomorphic preimage X is also locally compact Hausdorff. Moreover, if X were compact then c(X) would be closed in Y and hence not dense. Thus a space can only admit a one-point compactification if it is locally compact, noncompact and Hausdorff. Moreover, in such a one point compactification the image of a neighborhood basis for x in X gives a neighborhood basis for c(x) in c(X), and—because a subset of a compact Hausdorff space is compact if and only if it is closed—the open neighborhoods of 
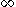must be all sets obtained by adjoining 
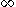to the image under c of a subset of X with compact complement.
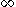be any object which is not already an element of X. (In terms of formal set theory one could take, for example, 
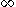to be X itself, but it is not really necessary or helpful to be so specific.) Put 
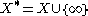, and topologize 
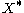by taking as open sets all the open subsets U of X together with all subsets V which contain 
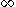and such that 
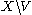is closed and compact, .
The inclusion map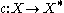
is called the Alexandroff extension of X (Willard, 19A).
The above properties all follow easily from the above discussion:
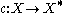is a compactification of X if and only if X is Hausdorff, noncompact and locally compact. In this case it is called the one-point compactification or Alexandroff compactification of X. Recall from the above discussion that any compactification
with one point remainder is necessarily (isomorphic to) the Alexandroff compactification.
Let X be any noncompact Tychonoff space. Under the natural partial ordering on the set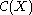
of equivalence classes of compactifications, any minimal element is equivalent to the Alexandroff extension (Engelking, Theorem 3.5.12). It follows that a noncompact Tychonoff space admits a minimal compactification if and only if it is locally compact.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, the Alexandroff extension is a way to extend a noncompact topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
by adjoining a single point in such a way that the resulting space is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
. It is named for the Russian mathematician Pavel Alexandrov.
More precisely, let X be a topological space. Then the Alexandroff extension of X is a certain compact space X* together with an open embedding c : X → X* such that the complement of X in X* consists of a single point, typically denoted ∞. The map c is a Hausdorff compactification
Compactification (mathematics)
In mathematics, compactification is the process or result of making a topological space compact. The methods of compactification are various, but each is a way of controlling points from "going off to infinity" by in some way adding "points at infinity" or preventing such an "escape".-An...
if and only if X is a locally compact, noncompact Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
. For such spaces the Alexandroff extension is called the one-point compactification or Alexandroff compactification. The advantages of the Alexandroff compactification lie in its simple, often geometrically meaningful structure and the fact that it is in a precise sense minimal among all compactifications; the disadvantage lies in the fact that it only gives a Hausdorff compactification on the class of locally compact, noncompact Hausdorff spaces, unlike the Stone–Čech compactification
Stone–Cech compactification
In the mathematical discipline of general topology, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact Hausdorff space βX...
which exists for any Tychonoff space
Tychonoff space
In topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
, a much larger class of spaces.
Example: inverse stereographic projection
A geometrically appealing example of one-point compactification is given by the inverse stereographic projectionStereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
. Recall that the stereographic projection S gives an explicit homeomorphism from the unit sphere minus the north pole (0,0,1) to the Euclidean plane. Therefore the inverse stereographic projection
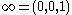is an open, dense embedding into a compact Hausdorff space obtained by adjoining the additional point . Under the stereographic projection latitudinal circles get mapped to planar circles 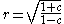. It follows that the deleted neighborhood basis of 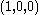given by the punctured spherical caps 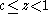corresponds to the complements of closed planar disks . More qualitatively, a neighborhood basis at 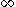is furnished by the sets 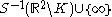as K ranges through the compact subsets of . This example already contains the key concepts of the general case.Motivation
Let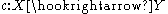 be an embedding from a topological space X to a compact Hausdorff topological space Y, with dense image and one-point remainder 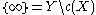. Then c(X) is open in a compact Hausdorff space so is locally compact Hausdorff, hence its homeomorphic preimage X is also locally compact Hausdorff. Moreover, if X were compact then c(X) would be closed in Y and hence not dense. Thus a space can only admit a one-point compactification if it is locally compact, noncompact and Hausdorff. Moreover, in such a one point compactification the image of a neighborhood basis for x in X gives a neighborhood basis for c(x) in c(X), and—because a subset of a compact Hausdorff space is compact if and only if it is closed—the open neighborhoods of 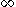must be all sets obtained by adjoining 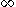to the image under c of a subset of X with compact complement.The Alexandroff extension
Let X be any topological space, and let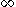 be any object which is not already an element of X. (In terms of formal set theory one could take, for example, 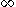to be X itself, but it is not really necessary or helpful to be so specific.) Put 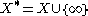, and topologize 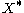by taking as open sets all the open subsets U of X together with all subsets V which contain 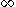and such that 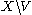is closed and compact, .The inclusion map
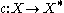is called the Alexandroff extension of X (Willard, 19A).The above properties all follow easily from the above discussion:
- The map c is continuous and open: it embeds X as an open subset of
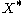. - The space
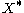is compact. - The image c(X) is dense in
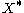, if X is noncompact. - The space
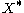is HausdorffHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
if and only if X is Hausdorff and locally compact.
The one-point compactification
In particular, the Alexandroff extension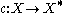 is a compactification of X if and only if X is Hausdorff, noncompact and locally compact. In this case it is called the one-point compactification or Alexandroff compactification of X. Recall from the above discussion that any compactificationwith one point remainder is necessarily (isomorphic to) the Alexandroff compactification.
Let X be any noncompact Tychonoff space. Under the natural partial ordering on the set
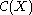of equivalence classes of compactifications, any minimal element is equivalent to the Alexandroff extension (Engelking, Theorem 3.5.12). It follows that a noncompact Tychonoff space admits a minimal compactification if and only if it is locally compact.Further examples
- The one-point compactification of the set of positive integers is homeomorphicHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to the space consisting of K = {0} U {1/n | n is a positive integer.} with the order topology.
- The one-point compactification of n-dimensional Euclidean space Rn is homeomorphic to the n-sphere Sn. As above, the map can be given explicitly as an n-dimensional inverse stereographic projection.
- Since the closure of a connected subset is connected, the Alexandroff extension of a noncompact connected space is connected. However a one-point compactification may "connect" a disconnected space: for instance the one-point compactification of the disjoint union of
copies of the interval (0,1) is a wedge of 
circlesBouquet of circlesIn mathematics, a rose is a topological space obtained by gluing together a collection of circles along a single point. The circles of the rose are called petals. Roses are important in algebraic topology, where they are closely related to free groups.- Definition :A rose is a wedge sum of circles...
.
- The Alexandroff extension can be viewed as a functor from the category of topological spaces to the category whose objects are continuous maps
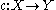and for which the morphisms from 
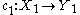to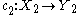 
are pairs of continuous maps 
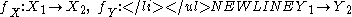such that 
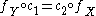. In particular, homeomorphic spaces have isomorphic Alexandroff extensions.
See also
- Wallman compactificationWallman compactificationIn mathematics, the Wallman compactification is a compactification of T1 topological spaces that was constructed by .The points of the Wallman compactification ωX of a space X are the maximal families Φ of closed nonempty subsets of X such that Φ is closed under finite intersections...
- End (topology)
- Riemann sphereRiemann sphereIn mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
- Normal spaceNormal spaceIn topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
- Stereographic projectionStereographic projectionThe stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
- Wallman compactification