In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

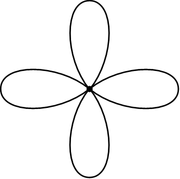
, a rose (also known as a bouquet of circles) is a topological space

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

 obtained by gluing

Quotient space

In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...

 together a collection of circles along a single point. The circles of the rose are called petals. Roses are important in algebraic topology

Algebraic topology

Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...

, where they are closely related to free group

Free group

In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...

s.

Definition

A rose is a wedge sum

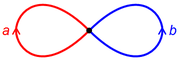
Wedge sum

In topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces the wedge sum of X and Y is the quotient of the disjoint union of X and Y by the identification x0 ∼ y0:X\vee Y = \;/ \sim,\,where ∼ is the...

 of circles. That is, the rose is the quotient space

Quotient space

In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...

 C/S, where C is a disjoint union of circles and S a set consisting of one point from each circle. As a cell complex, a rose has a single vertex, and one edge for each circle. This makes it a simple example of a topological graph.

A rose with n petals can also be obtained by identifying n points on a single circle. The rose with two petals is known as the figure eight.

Relation to free groups

The fundamental group

Fundamental group

In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...

 of a rose is free

Free group

In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...

, with one generator

Generating set of a group

In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...

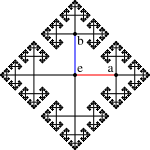
 for each petal. The universal cover is an infinite tree, which can be identified with the Cayley graph

Cayley graph

In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...

 of the free group. (This is a special case of the presentation complex

Presentation complex

In geometric group theory, a presentation complex is a 2-dimensional cell complex associated to any presentation of a group G. The complex has a single vertex, and one loop at the vertex for each generator of G...

 associated to any presentation of a group

Presentation of a group

In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...

.)

The intermediate covers of the rose correspond to subgroup

Subgroup

In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...

s of the free group. The observation that any cover of a rose is a graph provides a simple proof that every subgroup of a free group is free (the Nielsen–Schreier theorem

Nielsen–Schreier theorem

In group theory, a branch of mathematics, the Nielsen–Schreier theorem is the statement that every subgroup of a free group is itself free. It is named after Jakob Nielsen and Otto Schreier.-Statement of the theorem:...

)

Because the universal cover of a rose is contractible

Contractible space

In mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....

, the rose is actually an Eilenberg–MacLane space for the associated free group F. This implies that the cohomology

Group cohomology

In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...

 groups Hⁿ(F) are trivial for n ≥ 2.

Other properties

• Any connected
  Connectedness
  In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
  
   graph is homotopy equivalent to a rose. Specifically, the rose is the quotient space
  Quotient space
  In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
  
   of the graph obtained by collapsing a spanning tree
  Spanning tree (mathematics)
  In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
  
  .
• A disc
  Ball (mathematics)
  In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
  
   with n points removed (or a sphere
  Sphere
  A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
  
   with n + 1 points removed) deformation retract
  Deformation retract
  In topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...
  
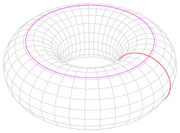
  s onto a rose with n petals. One petal of the rose surrounds each of the removed points.
• A torus
  Torus
  In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
  
   with one point removed deformation retracts onto a figure eight, namely the union of two generating circles. More generally, a surface of genus
  Genus (mathematics)
  In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
  
   g with one point removed deformation retracts onto a rose with 2g petals, namely the boundary of a fundamental polygon
  Fundamental polygon
  In mathematics, each closed surface in the sense of geometric topology can be constructed from an even-sided oriented polygon, called a fundamental polygon, by pairwise identification of its edges....
  
  .
• A rose can have infinitely many petals, leading to a fundamental group which is free on infinitely many generators. The rose with countably infinitely many petals is similar to the Hawaiian earring
  Hawaiian earring
  In mathematics, the Hawaiian earring H is the topological space defined by the union of circles in the Euclidean plane R2 with center and radius 1/n for n = 1, 2, 3, ......
  
  : there is a continuous bijection from this rose onto the Hawaiian earring, but the two are not homeomorphic.