Ammann–Beenker tiling
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, an Ammann–Beenker tiling is a nonperiodic tiling
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
generated by an aperiodic set
Aperiodic tiling
An aperiodic tiling is a tiling obtained from an aperiodic set of tiles. Properly speaking, aperiodicity is a property of particular sets of tiles; any given finite tiling is either periodic or non-periodic...
of prototile
Prototile
In the mathematical theory of tessellations, a prototile is one of the shapes of a tile in a tessellation.A tessellation of the plane or of any other space is a cover of the space by closed shapes, called tiles, that have disjoint interiors. Some of the tiles may be congruent to one or more others...
s named after Robert Ammann
Robert Ammann
Robert Ammann was an amateur mathematician who made several significant and groundbreaking contributions to the theory of quasicrystals and aperiodic tilings....
, who first discovered the tilings in the 1970s, and after F. P. M. Beenker who discovered them independently and showed how to obtain them by the cut-and-project method.
Because all tilings obtained with the tiles are non-periodic, Ammann–Beenker tilings are considered aperiodic tilings. They are one of the five sets of tilings discovered by Ammann and described in Tilings and Patterns.
The Ammann–Beenker tilings have many properties similar to the more famous Penrose tiling
Penrose tiling
A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles named after Sir Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original...
s, most notably:
- They are nonperiodic, which means that they lack any translational symmetryTranslational symmetryIn geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
. - Any finite region in a tiling appears infinitely many times in that tiling and, in fact, in any other tiling. Thus, the infinite tilings all look similar to one another, if one looks only at finite patches.
- They are quasicrystalQuasicrystalA quasiperiodic crystal, or, in short, quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry...
line: implemented as a physical structure an Ammann–Beenker tiling will produce Bragg diffraction; the diffractogram reveals both the underlying eightfold symmetry and the long-range order. This order reflects the fact that the tilings are organized, not through translational symmetry, but rather through a process sometimes called "deflation" or "inflation."
Various methods to construct the tilings have been proposed: matching rules, substitutions, cut and project schemes and coverings. In 1987 Wang, Chen and Kuo announced the discovery of a quasicrystal with octagonal symmetry .
Description of the tiles
The most common choice of tileset to produce the Ammann–Beenker tilings includes a rhombusRhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
with 45- and 135-degree angles (these rhombi are shown in white in the diagram at the top of the page) and a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
(shown in red in the diagram above). The square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
may alternatively be divided into a pair of isosceles right triangles. (This is also done in the above diagram.) The matching rules or substitution relations for the square/triangle do not respect all of its symmetries, however.
In fact, the matching rules for the tiles do not even respect the reflectional symmetries preserved by the substitution rules.
This is the substitution rule for the usual tileset.
An alternate set of tiles, also discovered by Ammann, and labelled "Ammann 4" in Grünbaum and Shephard, consists of two nonconvex right-angle-edged pieces. One consists of two squares overlapping on a smaller square, while the other consists of a large square attached to a smaller square. The diagrams below show the pieces and a portion of the tilings.
This is the substitution rule for the alternate tileset.
The relationship between the two tilesets.
In addition to the edge arrows in the usual tileset, the matching rules for both tilesets can be expressed by drawing pieces of large arrows at the vertices, and requiring them to piece together into full arrows.
Katz has studied the additional tilings allowed by dropping the vertex constraints and imposing only the requirement that the edge arrows match.
Pell and silver ratio features
The Ammann–Beenker tilings are closely related to the silver ratioSilver ratio
In mathematics, two quantities are in the silver ratio if the ratio between the sum of the smaller plus twice the larger of those quantities and the larger one is the same as the ratio between the larger one and the smaller. This defines the silver ratio as an irrational mathematical constant,...
(
) and the Pell numberPell number
In mathematics, the Pell numbers are an infinite sequence of integers that have been known since ancient times, the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins 1/1, 3/2, 7/5, 17/12, and 41/29, so the sequence of Pell numbers...
s.
- the substitutionSubstitutionSubstitution may refer to:- Sciences :* Substitution , a syntactic transformation on strings of symbols of a formal language* Substitution of variables* Substitution cipher, a method of encryption...
scheme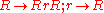
introduces the ratio as a scaling factor: its matrix is the Pell substitution matrix, and the series of words produced by the substitution have the property that the number of 
s and 
s are equal to successive Pell numbers. - the eigenvalues of the substitution matrix are
and 
. - In the alternate tileset, the long edges have
times longer sides than the short edges. - One set of ConwayJohn Horton ConwayJohn Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
worms, formed by the short and long diagonals of the rhombs, forms the above strings, with r as the short diagonal and R as the long diagonal. Therefore the Ammann bars also form Pell ordered grids.
The Ammann bars for the usual tileset. If the bold outer lines are taken to have length
, the bars split the edges into segments of length 
and 
.The Ammann bars for the alternate tileset. Note that the bars for the asymmetric tile extend partly outside it.
Cut-and-project construction
The hypercubic lattice has an eightfold rotational symmetry, corresponding to an eightfold rotational symmetry of the hypercubeHypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
. A rotation matrix representing this symmetry is:
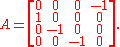
Transforming this matrix to the new coordinates given by
will produce: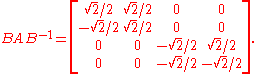
This third matrix then corresponds to a rotation both by 45° (in the first two dimensions) and by 135° (in the last two). We can then obtain an Ammann–Beenker tiling by projecting a slab of hypercubes along either the first two or the last two of the new coordinates.
Alternatively, an Ammann-Beenker tiling can be obtained by drawing rhombs and squares around the intersection points of pair of equal-scale square lattices overlaid at a 45-degree angle. These two techniques were developed by Beenker in his paper.