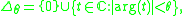Analytic semigroup
Encyclopedia
In mathematics
, an analytic semigroup is particular kind of strongly continuous semigroup. Analytic semigroups are used in the solution of partial differential equations; compared to strongly continuous semigroups, analytic semigroups provide better regularity
of solutions to initial value problems, better results concerning perturbations of the infinitesimal generator, and a relationship between the type of the semigroup and the spectrum
of the infinitesimal generator.
(X, ||·||) with infinitesimal generator A. Γ is said to be an analytic semigroup if
A closed
, densely-defined
linear operator A on a Banach space X is the generator of an analytic semigroup if and only if
there exists an ω ∈ R such that the half-plane Re(λ) > ω is contained in the resolvent set
of A and, moreover, there is a constant C such that
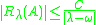
for Re(λ) > ω. If this is the case, then the resolvent set actually contains a sector of the form

for some δ > 0, and an analogous resolvent estimate holds in this sector. Moreover, the semigroup is represented by

where γ is any curve from e−iθ∞ to e+iθ∞ such that γ lies entirely in the sector

with π ⁄ 2 < θ < π ⁄ 2 + δ.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an analytic semigroup is particular kind of strongly continuous semigroup. Analytic semigroups are used in the solution of partial differential equations; compared to strongly continuous semigroups, analytic semigroups provide better regularity
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
of solutions to initial value problems, better results concerning perturbations of the infinitesimal generator, and a relationship between the type of the semigroup and the spectrum
Spectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
of the infinitesimal generator.
Definition
Let Γ(t) = exp(At) be a strongly continuous one-parameter semigroup on a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
(X, ||·||) with infinitesimal generator A. Γ is said to be an analytic semigroup if
- for some 0 < θ < π ⁄ 2, the continuous linear operatorContinuous linear operatorIn functional analysis and related areas of mathematics, a continuous linear operator or continuous linear mapping is a continuous linear transformation between topological vector spaces....
exp(At) : X → X can be extended to t ∈ Δθ,
- and the usual semigroup conditions hold for s, t ∈ Δθ: exp(A0) = id, exp(A(t + s)) = exp(At)exp(As), and, for each x ∈ X, exp(At)x is continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
in t;
- and, for all t ∈ Δθ \ {0}, exp(At) is analyticAnalytic functionIn mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
in t in the sense of the uniform operator topologyUniform topologyIn mathematics, the uniform topology on a space has several different meanings depending on the context:* In functional analysis, it sometimes refers to a polar topology on a topological vector space....
.
Characterization
The infinitesimal generators of analytic semigroups have the following characterization:A closed
Closed operator
In mathematics, specifically in functional analysis, closed linear operators are an important class of linear operators on Banach spaces. They are more general than bounded operators, and therefore not necessarily continuous, but they still retain nice enough properties that one can define the...
, densely-defined
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
linear operator A on a Banach space X is the generator of an analytic semigroup if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there exists an ω ∈ R such that the half-plane Re(λ) > ω is contained in the resolvent set
Resolvent formalism
In mathematics, the resolvent formalism is a technique for applying concepts from complex analysis to the study of the spectrum of operators on Hilbert spaces and more general spaces....
of A and, moreover, there is a constant C such that
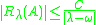
for Re(λ) > ω. If this is the case, then the resolvent set actually contains a sector of the form

for some δ > 0, and an analogous resolvent estimate holds in this sector. Moreover, the semigroup is represented by

where γ is any curve from e−iθ∞ to e+iθ∞ such that γ lies entirely in the sector

with π ⁄ 2 < θ < π ⁄ 2 + δ.