Artificial neuron
Encyclopedia
An artificial neuron is a mathematical function conceived as a crude model, or abstraction of biological neuron
s. Artificial neurons are the constitutive units in an artificial neural network
. Depending on the specific model used, it can receive different names, such as semi-linear unit, Nv neuron, binary neuron, linear threshold function or McCulloch–Pitts (MCP) neuron . The artificial neuron receives one or more inputs (representing the one or more dendrite
s) and sums them to produce an output (representing a biological neuron's axon
). Usually the sums of each node are weighted, and the sum is passed through a non-linear function known as an activation function
or transfer function
. The transfer functions usually have a sigmoid shape
, but they may also take the form of other non-linear functions, piecewise
linear functions, or step functions. They are also often monotonically increasing
, continuous
, differentiable
and bounded
.
The artificial neuron transfer function should not be confused with a linear system's transfer function
.
The output of kth neuron is:
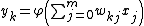
Where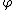
(phi) is the transfer function.
The output is analogous to the axon
of a biological neuron, and its value propagates to input of the next layer, through a synapse. It may also exit the system, possibly as part of an output vector.
It has no learning process as such. It cannot decide its own, here weights are calculated and accordingly the threshold value is calculated.
in 1943. As a transfer function, it employed a threshold, equivalent to using the Heaviside step function
. Initially, only a simple model was considered, with binary inputs and outputs, some restrictions on the possible weights, and a more flexible threshold value. Since the beginning it was already noticed that any boolean function could be implemented by networks of such devices, what is easily seen from the fact that one can implement the AND and OR functions, and use them in the disjunctive or the conjunctive normal form
.
Researchers also soon realized that cyclic networks, with feedback
s through neurons, could define dynamical systems with memory, but most of the research concentrated (and still does) on strictly feed-forward networks because of the smaller difficulty they present.
One important and pioneering artificial neural network that used the linear threshold function was the perceptron
, developed by Frank Rosenblatt
. This model already considered more flexible weight values in the neurons, and was used in machines with adaptive capabilities. The representation of the threshold values as a bias term was introduced by Widrow in 1960.
In the late 1980s, when research on neural networks regained strength, neurons with more continuous shapes started to be considered. The possibility of differentiating the activation function allows the direct use of the gradient descent
and other optimization algorithms for the adjustment of the weights. Neural networks also started to be used as a general function approximation model.
using a linear transfer function has an equivalent single-layer network; a non-linear function is therefore necessary to gain the advantages of a multi-layer network.
Below, u refers in all cases to the weighted sum of all the inputs to the neuron, i.e. for n inputs,
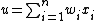
where w is a vector of synaptic weights and x is a vector of inputs.
This function is used in perceptron
s and often shows up in many other models. It performs a division of the space
of inputs by a hyperplane
. It is specially useful in the last layer of a network intended to perform binary classification of the inputs. It can be approximated from other sigmoidal functions by assigning large values to the weights.
, and they can all be used in neural networks with this linear neuron. The bias term allows us to make affine transformations
to the data.
See: Linear transformation
, Harmonic analysis
, Linear filter
, Wavelet
, Principal component analysis, Independent component analysis
, Deconvolution
.
such as the logistic function also has an easily calculated derivative, which can be important when calculating the weight updates in the network. It thus makes the network more easily manipulable mathematically, and was attractive to early computer scientists who needed to minimize the computational load of their simulations. It is commonly seen in multilayer perceptron
s using a backpropagation
algorithm.
See: Sigmoid function
implementation of a single TLU which takes boolean inputs (true or false), and returns a single boolean output when activated. An object-oriented model is used. No method of training is defined, since several exist. If a purely functional model were used, the class TLU below would be replaced with a function TLU with input parameters threshold, weights, and inputs that returned a boolean value.
class TLU defined as:
data member threshold : number
data member weights : list of numbers of size X
function member fire( inputs : list of booleans of size X ) : boolean defined as:
variable T : number
T ← 0
for each i in 1 to X :
if inputs(i) is true :
T ← T + weights(i)
end if
end for each
if T > threshold :
return true
else:
return false
end if
end function
end class
generated with :de:Wikipedia:Helferlein/VBA-Macro for EXCEL tableconversion V1.7<\hiddentext>>
Supervised neural network training for an OR gate.
Note: Initial weight equals final weight of previous iteration.
Neuron
A neuron is an electrically excitable cell that processes and transmits information by electrical and chemical signaling. Chemical signaling occurs via synapses, specialized connections with other cells. Neurons connect to each other to form networks. Neurons are the core components of the nervous...
s. Artificial neurons are the constitutive units in an artificial neural network
Artificial neural network
An artificial neural network , usually called neural network , is a mathematical model or computational model that is inspired by the structure and/or functional aspects of biological neural networks. A neural network consists of an interconnected group of artificial neurons, and it processes...
. Depending on the specific model used, it can receive different names, such as semi-linear unit, Nv neuron, binary neuron, linear threshold function or McCulloch–Pitts (MCP) neuron . The artificial neuron receives one or more inputs (representing the one or more dendrite
Dendrite
Dendrites are the branched projections of a neuron that act to conduct the electrochemical stimulation received from other neural cells to the cell body, or soma, of the neuron from which the dendrites project...
s) and sums them to produce an output (representing a biological neuron's axon
Axon
An axon is a long, slender projection of a nerve cell, or neuron, that conducts electrical impulses away from the neuron's cell body or soma....
). Usually the sums of each node are weighted, and the sum is passed through a non-linear function known as an activation function
Activation function
In computational networks, the activation function of a node defines the output of that node given an input or set of inputs. A standard computer chip circuit can be seen as a digital network of activation functions that can be "ON" or "OFF" , depending on input. This is similar to the behavior of...
or transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
. The transfer functions usually have a sigmoid shape
Sigmoid function
Many natural processes, including those of complex system learning curves, exhibit a progression from small beginnings that accelerates and approaches a climax over time. When a detailed description is lacking, a sigmoid function is often used. A sigmoid curve is produced by a mathematical...
, but they may also take the form of other non-linear functions, piecewise
Piecewise
On mathematics, a piecewise-defined function is a function whose definition changes depending on the value of the independent variable...
linear functions, or step functions. They are also often monotonically increasing
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
, continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, differentiable
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
and bounded
Bounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
.
The artificial neuron transfer function should not be confused with a linear system's transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
.
Basic structure
For a given artificial neuron, let there be m + 1 inputs with signals x0 through xm and weights w0 through wm. Usually, the x0 input is assigned the value +1, which makes it a bias input with wk0 = bk. This leaves only m actual inputs to the neuron: from x1 to xm.The output of kth neuron is:
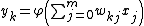
Where
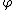(phi) is the transfer function.The output is analogous to the axon
Axon
An axon is a long, slender projection of a nerve cell, or neuron, that conducts electrical impulses away from the neuron's cell body or soma....
of a biological neuron, and its value propagates to input of the next layer, through a synapse. It may also exit the system, possibly as part of an output vector.
It has no learning process as such. It cannot decide its own, here weights are calculated and accordingly the threshold value is calculated.
History
The first artificial neuron was the Threshold Logic Unit (TLU) first proposed by Warren McCulloch and Walter PittsWalter Pitts
Walter Harry Pitts, Jr. was a logician who worked in the field of cognitive psychology.He proposed landmark theoretical formulations of neural activity and emergent processes that influenced diverse fields such as cognitive sciences and psychology, philosophy, neurosciences, computer science,...
in 1943. As a transfer function, it employed a threshold, equivalent to using the Heaviside step function
Heaviside step function
The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
. Initially, only a simple model was considered, with binary inputs and outputs, some restrictions on the possible weights, and a more flexible threshold value. Since the beginning it was already noticed that any boolean function could be implemented by networks of such devices, what is easily seen from the fact that one can implement the AND and OR functions, and use them in the disjunctive or the conjunctive normal form
Conjunctive normal form
In Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
.
Researchers also soon realized that cyclic networks, with feedback
Feedback
Feedback describes the situation when output from an event or phenomenon in the past will influence an occurrence or occurrences of the same Feedback describes the situation when output from (or information about the result of) an event or phenomenon in the past will influence an occurrence or...
s through neurons, could define dynamical systems with memory, but most of the research concentrated (and still does) on strictly feed-forward networks because of the smaller difficulty they present.
One important and pioneering artificial neural network that used the linear threshold function was the perceptron
Perceptron
The perceptron is a type of artificial neural network invented in 1957 at the Cornell Aeronautical Laboratory by Frank Rosenblatt. It can be seen as the simplest kind of feedforward neural network: a linear classifier.- Definition :...
, developed by Frank Rosenblatt
Frank Rosenblatt
Frank Rosenblatt was a New York City born computer scientist who completed the Perceptron, or MARK 1, computer at Cornell University in 1960...
. This model already considered more flexible weight values in the neurons, and was used in machines with adaptive capabilities. The representation of the threshold values as a bias term was introduced by Widrow in 1960.
In the late 1980s, when research on neural networks regained strength, neurons with more continuous shapes started to be considered. The possibility of differentiating the activation function allows the direct use of the gradient descent
Gradient descent
Gradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
and other optimization algorithms for the adjustment of the weights. Neural networks also started to be used as a general function approximation model.
Types of transfer functions
The transfer function of a neuron is chosen to have a number of properties which either enhance or simplify the network containing the neuron. Crucially, for instance, any multilayer perceptronMultilayer perceptron
A multilayer perceptron is a feedforward artificial neural network model that maps sets of input data onto a set of appropriate output. An MLP consists of multiple layers of nodes in a directed graph, with each layer fully connected to the next one. Except for the input nodes, each node is a...
using a linear transfer function has an equivalent single-layer network; a non-linear function is therefore necessary to gain the advantages of a multi-layer network.
Below, u refers in all cases to the weighted sum of all the inputs to the neuron, i.e. for n inputs,
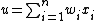
where w is a vector of synaptic weights and x is a vector of inputs.
Step function
The output y of this transfer function is binary, depending on whether the input meets a specified threshold, θ. The "signal" is sent, i.e. the output is set to one, if the activation meets the threshold.This function is used in perceptron
Perceptron
The perceptron is a type of artificial neural network invented in 1957 at the Cornell Aeronautical Laboratory by Frank Rosenblatt. It can be seen as the simplest kind of feedforward neural network: a linear classifier.- Definition :...
s and often shows up in many other models. It performs a division of the space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of inputs by a hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
. It is specially useful in the last layer of a network intended to perform binary classification of the inputs. It can be approximated from other sigmoidal functions by assigning large values to the weights.
Linear combination
In this case, the output unit is simply the weighted sum of its inputs plus a bias term. A number of such linear neurons perform a linear transformation of the input vector. This is usually more useful in the first layers of a network. A number of analysis tools exist based on linear models, such as harmonic analysisHarmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
, and they can all be used in neural networks with this linear neuron. The bias term allows us to make affine transformations
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
to the data.
See: Linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
, Harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
, Linear filter
Linear filter
Linear filters in the time domain process time-varying input signals to produce output signals, subject to the constraint of linearity.This results from systems composed solely of components classified as having a linear response....
, Wavelet
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
, Principal component analysis, Independent component analysis
Independent component analysis
Independent component analysis is a computational method for separating a multivariate signal into additive subcomponents supposing the mutual statistical independence of the non-Gaussian source signals...
, Deconvolution
Deconvolution
In mathematics, deconvolution is an algorithm-based process used to reverse the effects of convolution on recorded data. The concept of deconvolution is widely used in the techniques of signal processing and image processing...
.
Sigmoid
A fairly simple non-linear function, a Sigmoid functionSigmoid function
Many natural processes, including those of complex system learning curves, exhibit a progression from small beginnings that accelerates and approaches a climax over time. When a detailed description is lacking, a sigmoid function is often used. A sigmoid curve is produced by a mathematical...
such as the logistic function also has an easily calculated derivative, which can be important when calculating the weight updates in the network. It thus makes the network more easily manipulable mathematically, and was attractive to early computer scientists who needed to minimize the computational load of their simulations. It is commonly seen in multilayer perceptron
Multilayer perceptron
A multilayer perceptron is a feedforward artificial neural network model that maps sets of input data onto a set of appropriate output. An MLP consists of multiple layers of nodes in a directed graph, with each layer fully connected to the next one. Except for the input nodes, each node is a...
s using a backpropagation
Backpropagation
Backpropagation is a common method of teaching artificial neural networks how to perform a given task. Arthur E. Bryson and Yu-Chi Ho described it as a multi-stage dynamic system optimization method in 1969 . It wasn't until 1974 and later, when applied in the context of neural networks and...
algorithm.
See: Sigmoid function
Sigmoid function
Many natural processes, including those of complex system learning curves, exhibit a progression from small beginnings that accelerates and approaches a climax over time. When a detailed description is lacking, a sigmoid function is often used. A sigmoid curve is produced by a mathematical...
Pseudocode algorithm
The following is a simple pseudocodePseudocode
In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
implementation of a single TLU which takes boolean inputs (true or false), and returns a single boolean output when activated. An object-oriented model is used. No method of training is defined, since several exist. If a purely functional model were used, the class TLU below would be replaced with a function TLU with input parameters threshold, weights, and inputs that returned a boolean value.
class TLU defined as:
data member threshold : number
data member weights : list of numbers of size X
function member fire( inputs : list of booleans of size X ) : boolean defined as:
variable T : number
T ← 0
for each i in 1 to X :
if inputs(i) is true :
T ← T + weights(i)
end if
end for each
if T > threshold :
return true
else:
return false
end if
end function
end class
Spreadsheet example
| Input | Initial | Output | Final | |||||||||||
| Threshold | Learning Rate | Sensor values | Desired output | Weights | Calculated | Sum | Network | Error | Correction | Weights | ||||
| TH | LR | X1 | X2 | Z | w1 | w2 | C1 | C2 | S | N | E | R | W1 | W2 |
||||||||||||||
| | | | | | | X1 x w1 | X2 x w2 | C1+C2 | IF(S>TH,1,0) | Z-N | LR x E | R+w1 | R+w2 |
||||||||||||||
| 0.5 | 0.2 | 0 | 0 | 0 | 0.1 | 0.3 | 0 | 0 | 0 | 0 | 0 | 0 | 0.1 | 0.3 |
||||||||||||||
| 0.5 | 0.2 | 0 | 1 | 1 | 0.1 | 0.3 | 1 | 0.3 | 0.3 | 0 | 1 | 0.2 | 0.3 | 0.5 |
||||||||||||||
| 0.5 | 0.2 | 1 | 0 | 1 | 0.3 | 0.5 | 0.3 | 0 | 0.3 | 0 | 1 | 0.2 | 0.5 | 0.7 |
||||||||||||||
| 0.5 | 0.2 | 1 | 1 | 1 | 0.5 | 0.7 | 0.5 | 0.7 | 1.2 | 1 | 0 | 0 | 0.5 | 0.7 |
||||||||||||||
| 0.5 | 0.2 | 0 | 0 | 0 | 0.5 | 0.7 | 0 | 0 | 0 | 0 | 0 | 0 | 0.5 | 0.7 |
||||||||||||||
| 0.5 | 0.2 | 0 | 1 | 1 | 0.5 | 0.7 | 0 | 0.7 | 0.7 | 1 | 0 | 0 | 0.5 | 0.7 |
||||||||||||||
| 0.5 | 0.2 | 1 | 0 | 1 | 0.5 | 0.7 | 0.5 | 0 | 0.5 | 0 | 1 | 0.2 | 0.7 | 0.9 |
||||||||||||||
| 0.5 | 0.2 | 1 | 1 | 1 | 0.7 | 0.9 | 0.7 | 0.9 | 1.6 | 1 | 0 | 0 | 0.7 | 0.9 |
||||||||||||||
| 0.5 | 0.2 | 0 | 0 | 0 | 0.7 | 0.9 | 0 | 0 | 0 | 0 | 0 | 0 | 0.7 | 0.9 |
||||||||||||||
| 0.5 | 0.2 | 0 | 1 | 1 | 0.7 | 0.9 | 0 | 0.9 | 0.9 | 1 | 0 | 0 | 0.7 | 0.9 |
||||||||||||||
| 0.5 | 0.2 | 1 | 0 | 1 | 0.7 | 0.9 | 0.7 | 0 | 0.7 | 1 | 0 | 0 | 0.7 | 0.9 |
||||||||||||||
| 0.5 | 0.2 | 1 | 1 | 1 | 0.7 | 0.9 | 0.7 | 0.9 | 1.6 | 1 | 0 | 0 | 0.7 | 0.9 |
||||||||||||||
Supervised neural network training for an OR gate.
Note: Initial weight equals final weight of previous iteration.
Limitations
Artificial neurons of simple types, such as the McCulloch–Pitts model, are sometimes characterized as "caricature models", in that they are intended to reflect one or more neurophysiological observations, but without regard to realism.See also
- Neural networkNeural networkThe term neural network was traditionally used to refer to a network or circuit of biological neurons. The modern usage of the term often refers to artificial neural networks, which are composed of artificial neurons or nodes...
- PerceptronPerceptronThe perceptron is a type of artificial neural network invented in 1957 at the Cornell Aeronautical Laboratory by Frank Rosenblatt. It can be seen as the simplest kind of feedforward neural network: a linear classifier.- Definition :...
- ADALINEADALINEADALINE is a single layer neural network. It was developed by Professor Bernard Widrow and his graduate student Ted Hoff at Stanford University in 1960. It is based on the McCulloch–Pitts neuron...
- Biological neuron models
- ConnectionismConnectionismConnectionism is a set of approaches in the fields of artificial intelligence, cognitive psychology, cognitive science, neuroscience and philosophy of mind, that models mental or behavioral phenomena as the emergent processes of interconnected networks of simple units...
Further reading
- McCulloch, W. and Pitts, WWalter PittsWalter Harry Pitts, Jr. was a logician who worked in the field of cognitive psychology.He proposed landmark theoretical formulations of neural activity and emergent processes that influenced diverse fields such as cognitive sciences and psychology, philosophy, neurosciences, computer science,...
. (1943). A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biophysics, 7:115 - 133. - A.S. Samardak, A. Nogaret, N. B. Janson, A. G. Balanov, I. Farrer and D. A. Ritchie. "Noise-Controlled Signal Transmission in a Multithread Semiconductor Neuron" // Phys.Rev.Lett. 102 (2009) 226802, http://prl.aps.org/abstract/PRL/v102/i22/e226802
External links
- http://www.mind.ilstu.edu/curriculum/modOverview.php?modGUI=212 A good general overview