
Banach-Stone theorem
Encyclopedia
In mathematics
, the Banach–Stone theorem is a classical result in the theory of continuous function
s on topological space
s, named after the mathematician
s Stefan Banach
and Marshall Stone
.
In brief, the Banach–Stone theorem allows one to recover a compact Hausdorff space from the algebra of scalars (the bounded continuous functions on the space). In modern language, this is the commutative case of the spectrum of a C*-algebra, and the Banach–Stone theorem can be seen as a functional analysis analog of the connection between a ring R and the spectrum of a ring
Spec(R) in algebraic geometry
.
, bounded function
s f : X → R equipped with the supremum norm ||·||∞. This is an algebra, called the algebra of scalars, under pointwise multiplication of functions. For a compact space
X, Cb(X; R) is the same as C(X; R), the space of all continuous functions f : X → R. The algebra of scalars is a functional analysis analog of the ring of regular function
s in algebraic geometry, there denoted .
.
Let X and Y be compact
, Hausdorff space
s and let T : C(X; R) → C(Y; R) be a surjective
linear isometry. Then there exists a homeomorphism
φ : Y → X and g ∈ C(Y; R) with

and
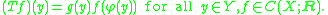
with trivial centralizer
and X and Y are compact, then every linear isometry of C(X; E) onto C(Y; E) is a strong Banach–Stone map.
More significantly, the Banach–Stone theorem suggests the philosophy that one can replace a space (a geometric notion) by an algebra, with no loss. Reversing this, it suggests that one can consider algebraic objects, even if they do not come from a geometric object, as a kind of "algebra of scalars". In this vein, any commutative C*-algebra is the algebra of scalars on a Hausdorff space. Thus one may consider noncommutative C*-algebras (and their Spec) as non-commutative spaces. This is the basis of the field of noncommutative geometry
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Banach–Stone theorem is a classical result in the theory of continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s on topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s, named after the mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s Stefan Banach
Stefan Banach
Stefan Banach was a Polish mathematician who worked in interwar Poland and in Soviet Ukraine. He is generally considered to have been one of the 20th century's most important and influential mathematicians....
and Marshall Stone
Marshall Harvey Stone
Marshall Harvey Stone was an American mathematician who contributed to real analysis, functional analysis, and the study of Boolean algebras.-Biography:...
.
In brief, the Banach–Stone theorem allows one to recover a compact Hausdorff space from the algebra of scalars (the bounded continuous functions on the space). In modern language, this is the commutative case of the spectrum of a C*-algebra, and the Banach–Stone theorem can be seen as a functional analysis analog of the connection between a ring R and the spectrum of a ring
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
Spec(R) in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
.
Statement of the theorem
For a topological space X, let Cb(X; R) denote the normed vector space of continuous, real-valuedReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, bounded function
Bounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
s f : X → R equipped with the supremum norm ||·||∞. This is an algebra, called the algebra of scalars, under pointwise multiplication of functions. For a compact space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
X, Cb(X; R) is the same as C(X; R), the space of all continuous functions f : X → R. The algebra of scalars is a functional analysis analog of the ring of regular function
Regular function
In mathematics, a regular function is a function that is analytic and single-valued in a given region. In complex analysis, any complex regular function is known as a holomorphic function...
s in algebraic geometry, there denoted
 .
.Let X and Y be compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s and let T : C(X; R) → C(Y; R) be a surjective
Surjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
linear isometry. Then there exists a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
φ : Y → X and g ∈ C(Y; R) with

and
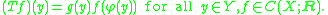
Generalizations
The Banach–Stone theorem has some generalizations for vector-valued continuous functions on compact, Hausdorff topological spaces. For example, if E is a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
with trivial centralizer
Multipliers and centralizers (Banach spaces)
In mathematics, multipliers and centralizers are algebraic objects in the study of Banach spaces. They are used, for example, in generalizations of the Banach-Stone theorem.-Definitions:...
and X and Y are compact, then every linear isometry of C(X; E) onto C(Y; E) is a strong Banach–Stone map.
More significantly, the Banach–Stone theorem suggests the philosophy that one can replace a space (a geometric notion) by an algebra, with no loss. Reversing this, it suggests that one can consider algebraic objects, even if they do not come from a geometric object, as a kind of "algebra of scalars". In this vein, any commutative C*-algebra is the algebra of scalars on a Hausdorff space. Thus one may consider noncommutative C*-algebras (and their Spec) as non-commutative spaces. This is the basis of the field of noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
.

