Base locus
Encyclopedia
In mathematics
, specifically algebraic geometry
, the base locus of a linear system of divisors
on a variety
refers to the subvariety of points 'common' to all divisors in the linear system.
Geometrically, this corresponds to the common intersection of the varieties.
is a linear system of divisors on some variety 
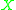. Consider the intersection
where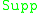
denotes the support of a divisor, and the intersection is taken over all effective divisors 
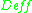in the linear system. This is the base locus of 
(as a set, at least: there may be more subtle scheme-theoretic
considerations as to what the structure sheaf
of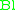
should be).
One application of the notion of base locus is to nefness
of a Cartier divisor class (i.e. complete linear system). Suppose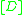
is such a class on a variety 
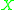, and 
an irreducible curve on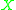 
. If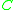 
is not contained in the base locus of 
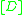, then there exists some divisor 
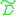in the class which does not contain 
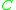, and so intersects it properly. Basic facts from intersection theory then tell us that we must have 
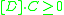. The conclusion is that to check nefness of a divisor class, it suffices to compute the intersection number with curves contained in the base locus of the class. So, roughly speaking, the 'smaller' the base locus, the 'more likely' it is that the class is nef.
In the modern formulation of algebraic geometry, a linear system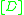
of (Cartier) divisors on a variety 
is viewed as a line bundle 
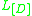on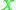 
. From this viewpoint, the base locus 
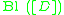is the set of common zeroes of all sections of 
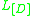. A simple consequence is that the bundle is globally generated
if and only if the base locus is empty.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the base locus of a linear system of divisors
Linear system of divisors
In algebraic geometry, a linear system of divisors is an algebraic generalization of the geometric notion of a family of curves; the dimension of the linear system corresponds to the number of parameters of the family....
on a variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
refers to the subvariety of points 'common' to all divisors in the linear system.
Geometrically, this corresponds to the common intersection of the varieties.
Definition
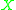More precisely, suppose that is a linear system of divisors on some variety . Consider the intersection
where
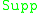denotes the support of a divisor, and the intersection is taken over all effective divisors 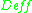in the linear system. This is the base locus of (as a set, at least: there may be more subtle scheme-theoreticScheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
considerations as to what the structure sheaf
Ringed space
In mathematics, a ringed space is, intuitively speaking, a space together with a collection of commutative rings, the elements of which are "functions" on each open set of the space...
of
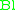should be).One application of the notion of base locus is to nefness
Numerically effective
A line bundle on an algebraic variety is said to be nef , if the degree of the restriction to any algebraic curve of the variety is non-negative.In particular, every ample line bundle is nef....
of a Cartier divisor class (i.e. complete linear system). Suppose
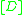is such a class on a variety 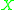, and an irreducible curve on 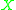. If 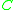is not contained in the base locus of 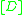, then there exists some divisor 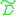in the class which does not contain 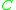, and so intersects it properly. Basic facts from intersection theory then tell us that we must have 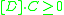. The conclusion is that to check nefness of a divisor class, it suffices to compute the intersection number with curves contained in the base locus of the class. So, roughly speaking, the 'smaller' the base locus, the 'more likely' it is that the class is nef.In the modern formulation of algebraic geometry, a linear system
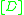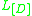of (Cartier) divisors on a variety is viewed as a line bundle on 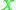. From this viewpoint, the base locus 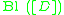is the set of common zeroes of all sections of 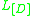. A simple consequence is that the bundle is globally generatedAmple line bundle
In algebraic geometry, a very ample line bundle is one with enough global sections to set up an embedding of its base variety or manifold M into projective space. An ample line bundle is one such that some positive power is very ample...
if and only if the base locus is empty.