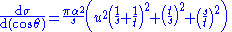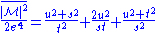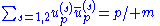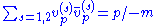Bhabha scattering
Encyclopedia
| Feynman diagrams |
|---|
Annihilation |
Scattering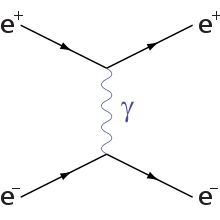 |
| Note: Time moves forward from the left side of the diagram to the right. The arrows are simply markers of particle motion, and are not the same as the arrows conventionally written into Feynman diagrams. |
In quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
, Bhabha scattering is the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
-positron
Positron
The positron or antielectron is the antiparticle or the antimatter counterpart of the electron. The positron has an electric charge of +1e, a spin of ½, and has the same mass as an electron...
scattering
Scattering
Scattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...
process:
There are two leading-order Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s contributing to this interaction: an annihilation process and a scattering process. The Bhabha scattering rate is used as a luminosity
Luminosity
Luminosity is a measurement of brightness.-In photometry and color imaging:In photometry, luminosity is sometimes incorrectly used to refer to luminance, which is the density of luminous intensity in a given direction. The SI unit for luminance is candela per square metre.The luminosity function...
monitor in electron-positron colliders.
Bhabha scattering is named after Indian physicist Homi J. Bhabha
Homi J. Bhabha
Homi Jehangir Bhabha, FRS was an Indian nuclear physicist and the chief architect of the Indian atomic energy program...
.
Differential cross section
To leading order, the spin-averaged differential cross section for this process is- where s,t, and u are the Mandelstam variablesMandelstam variablesIn theoretical physics, the Mandelstam variables are numerical quantities that encode the energy, momentum, and angles of particles in a scattering process in a Lorentz-invariant fashion...
, is the fine-structure constantFine-structure constantIn physics, the fine-structure constant is a fundamental physical constant, namely the coupling constant characterizing the strength of the electromagnetic interaction. Being a dimensionless quantity, it has constant numerical value in all systems of units...
is the fine-structure constantFine-structure constantIn physics, the fine-structure constant is a fundamental physical constant, namely the coupling constant characterizing the strength of the electromagnetic interaction. Being a dimensionless quantity, it has constant numerical value in all systems of units...
, and is the scattering angle.
is the scattering angle.
This cross section is calculated neglecting the electron mass relative to the collision energy and including only the contribution from photon exchange. This is a valid approximation at collision energies small compared to the mass scale of the Z boson, about 91 GeV; for energies not too small compared to this mass, the contribution from Z boson exchange also becomes important.
Mandelstam variables
In this article, the Mandelstam variablesMandelstam variables
In theoretical physics, the Mandelstam variables are numerical quantities that encode the energy, momentum, and angles of particles in a scattering process in a Lorentz-invariant fashion...
are defined by
|align="right"|

|align="right"|
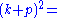
|align="right"|
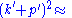
|align="right"|
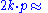
|align="right"|
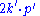
|rowspan="3"|

|-
|align="right"|
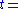
|align="right"|
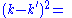
|align="right"|
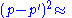
|
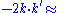
|
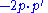
|-
|align="right"|

|align="right"|

|align="right"|
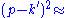
|
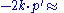
|
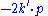
|}
Where the approximations are for the high-energy (relativistic) limit.
Matrix elements
Both diagrams contribute to the transition matrix element. By letting k and k' represent the four-momentum of the positron, while letting p and p' represent the four-momentum of the electron, and by using Feynman rules one can show the following diagrams give these matrix elements: 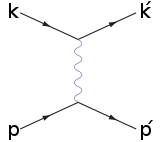 |
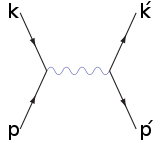 |
Where we use: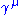 are the Gamma matrices, are the Gamma matrices,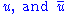 are the four-component spinors for fermions, while are the four-component spinors for fermions, while are the four-component spinors for anti-fermions (see Four spinors). are the four-component spinors for anti-fermions (see Four spinors). |
|
| (scattering) | (annihilation) | ||
 |
 |
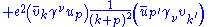 |
Notice that there is a relative sign difference between the two diagrams.
Square of matrix element
To calculate the unpolarized cross sectionCross section (physics)
A cross section is the effective area which governs the probability of some scattering or absorption event. Together with particle density and path length, it can be used to predict the total scattering probability via the Beer-Lambert law....
, one must average over the spins of the incoming particles (se- and se+ possible values) and sum over the spins of the outgoing particles. That is,
|
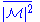
|
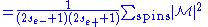
|-
|
|
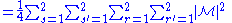
|}
First, calculate
 :
:
-
- {| cellpadding=4
|
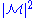 =
=|
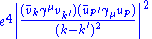
| align="center" | (scattering)
|-
|
|
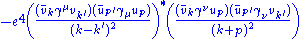
| align="center" | (interference)
|-
|
|
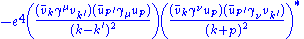
| align="center" | (interference)
|-
|
|
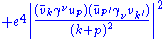
| align="center" | (annihilation)
|}
Magnitude squared of M
|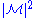
|
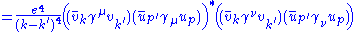
|
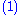
|-
|
|
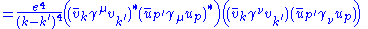
|
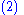
|-
|
|align="center" | (complex conjugate will flip order)
|
|-
|
|
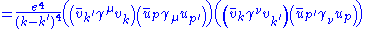
|
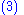
|-
|
|align="center" | (move terms that depend on same momentum to be next to each other)
|
|-
|
|

|
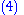
|}
Sum over spins
Next, we'd like to sum over spins of all four particles. Let s and s' be the spin of the electron and r and r' be the spin of the positron.|

|

|

|-
|
|

|
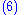
|-
|
|align="center" | (now use Completeness relations)
|
|-
|
|
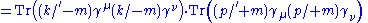
|
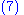
|-
|
|align="center" | (now use Trace identities)
|
|-
|
|
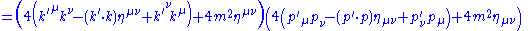
|

|-
|
|
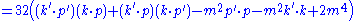
|

|}
Now that is the exact form, in the case of electrons one is usually interested in energy scales that far exceed the electron mass. Neglecting the electron mass yields the simplified form:
|

|
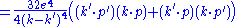
|-
|
|(use the Mandelstam variables in this relativistic limit)
|-
|
|
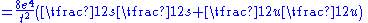
|-
|
|
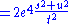
|}
Annihilation term (s-channel)
The process for finding the annihilation term is similar to the above. Since the two diagrams are related by crossing symmetryCrossing symmetry
In quantum field theory, a branch of theoretical physics, crossing is the property of scattering amplitudes that allows antiparticles to be interpreted as particles going backwards in time....
, and the initial and final state particles are the same, it is sufficient to permute the momenta, yielding
|

|

|-
|
|

|-
|
|
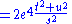
|}
Solution
Evaluating the interference term along the same lines and adding the three terms yields the final resultCompleteness relations
The completeness relations for the four-spinors u and v are-
- where
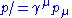 (see Feynman slash notation)
(see Feynman slash notation)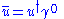
Trace identities
- Main article: Trace identities
To simplify the trace of the Dirac gamma matrices, one must use trace identities. Three used in this article are:
- The Trace of any product of an odd number of
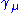 's is zero
's is zero 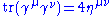
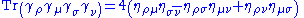
Using these two one finds that, for example,
|
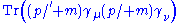
|
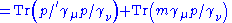
|-
|
|
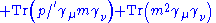
|-
|
|align="center"|(the two middle terms are zero because of (1))
|-
|
|
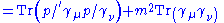
|-
|
|align="center"|(use identity (2) for the term on the right)
|-
|
|
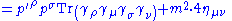
|-
|
|align="center"|(now use identity (3) for the term on the left)
|-
|
|

|-
|
|
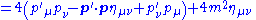
|}
Uses
Bhabha scattering has been used as a luminosityLuminosity
Luminosity is a measurement of brightness.-In photometry and color imaging:In photometry, luminosity is sometimes incorrectly used to refer to luminance, which is the density of luminous intensity in a given direction. The SI unit for luminance is candela per square metre.The luminosity function...
monitor in a number of e+e- collider physics experiments. The accurate measurement of luminosity is necessary for accurate measurements of cross sections.
- Small-angle Bhabha scattering was used to measure the luminosity of the 1993 run of the Stanford Large Detector (SLD), with a relative uncertainty of less than 0.5%.
- Electron-positron colliders operating in the region of the low-lying hadronic resonances (about 1 GeV to 10 GeV), such as the Beijing Electron Synchrotron (BES) and the BelleBelle experimentThe Belle experiment is a particle physics experiment conducted by the Belle Collaboration, an international collaboration of more than 400 physicists and engineers investigating CP-violation effects at the High Energy Accelerator Research Organisation in Tsukuba, Ibaraki Prefecture, Japan.The...
and BaBarBaBar experimentThe BaBar experiment, or simply BaBar, is an international collaboration of more than 500 physicists and engineers studying the subatomic world at energies of approximately ten times the rest mass of a proton . Its design was motivated by the investigation of CP violation...
"B-factory" experiments, use large-angle Bhabha scattering as a luminosity monitor. To achieve the desired precision at the 0.1% level, the experimental measurements must be compared to a theoretical calculation including next-to-leading-order radiative correctionsRenormalizationIn quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
.http://arxiv.org/abs/hep-ph/0003268 The high-precision measurement of the total hadronic cross section at these low energies is a crucial input into the theoretical calculation of the anomalous magnetic dipole momentAnomalous magnetic dipole momentIn quantum electrodynamics, the anomalous magnetic moment of a particle is a contribution of effects of quantum mechanics, expressed by Feynman diagrams with loops, to the magnetic moment of that particle...
of the muonMuonThe muon |mu]] used to represent it) is an elementary particle similar to the electron, with a unitary negative electric charge and a spin of ½. Together with the electron, the tau, and the three neutrinos, it is classified as a lepton...
, which is used to constrain supersymmetrySupersymmetryIn particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
and other models of physics beyond the Standard ModelBeyond the Standard ModelPhysics beyond the Standard Model refers to the theoretical developments needed to explain the deficiencies of the Standard Model, such as the origin of mass, the strong CP problem, neutrino oscillations, matter–antimatter asymmetry, and the nature of dark matter and dark energy...
.