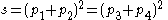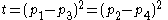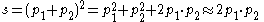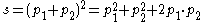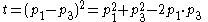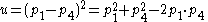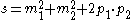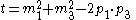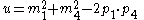Mandelstam variables
Encyclopedia
In theoretical physics
, the Mandelstam variables are numerical quantities that encode the energy
, momentum
, and angles of particles in a scattering process in a Lorentz-invariant fashion. They are used for scattering processes of two particles to two particles.
If the Minkowski Metric is chosen to be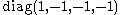 , the Mandelstam variables
, the Mandelstam variables 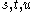 are then defined by
are then defined by
Where p1 and p2 are the four-momenta
of the incoming particles and p3 and p4 are the four-momenta of the outgoing particles, and we are using Planck units
(c=1).
s is also known as the square of the center-of-mass energy (invariant mass
) and t is also known as the square of the momentum transfer.
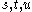 are also used in the terms s-channel, t-channel, u-channel. These channels represent different Feynman diagram
are also used in the terms s-channel, t-channel, u-channel. These channels represent different Feynman diagram
s or different possible scattering events where the interaction involves the exchange of an intermediate particle whose squared four-momentum equals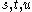 , respectively.
, respectively.
|
|
|
|-
|align="center"|s-channel
|align="center"|t-channel
|align="center"|u-channel
|}
For example the s-channel corresponds to the particles 1,2 joining into an intermediate particle that eventually splits into 3,4: the s-channel is the only way that resonances and new unstable particles may be discovered provided their lifetimes are long enough that they are directly detectable. The t-channel represents the process in which the particle 1 emits the intermediate particle and becomes the final particle 3, while the particle 2 absorbs the intermediate particle and becomes 4. The u-channel is the t-channel with the role of the particles 3,4 interchanged.
The Mandelstam variables were first introduced by physicist Stanley Mandelstam
in 1958.
because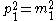 and
and 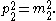 It is reminded that by relativistic limit one means that the momentum (speed) is so large that in the relativistic energy-momentum equation the energy becomes essentially the momentum norm (e.g.
It is reminded that by relativistic limit one means that the momentum (speed) is so large that in the relativistic energy-momentum equation the energy becomes essentially the momentum norm (e.g. 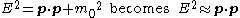 ).
).
In summary,
|align="right"|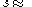
|align="right"|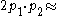
|align="right"|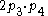
|-
|align="right"|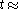
|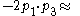
|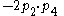
|-
|align="right"|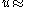
|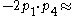
|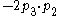
|}
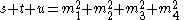
where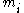 is the mass of particle
is the mass of particle  .
.
So, to begin,
First, use (1) to re-write these,
Then add them
|
|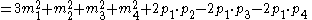
|-
|
|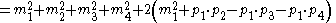
|-
|
|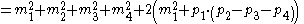
|}
Then use eq (2) to simplify further,
|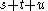
|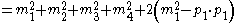
|-
|
|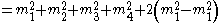
|}
So finally,
|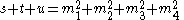
|}
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the Mandelstam variables are numerical quantities that encode the energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
, momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, and angles of particles in a scattering process in a Lorentz-invariant fashion. They are used for scattering processes of two particles to two particles.
If the Minkowski Metric is chosen to be
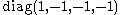 , the Mandelstam variables
, the Mandelstam variables 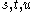 are then defined by
are then defined by
Where p1 and p2 are the four-momenta
Four-momentum
In special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime...
of the incoming particles and p3 and p4 are the four-momenta of the outgoing particles, and we are using Planck units
Planck units
In physics, Planck units are physical units of measurement defined exclusively in terms of five universal physical constants listed below, in such a manner that these five physical constants take on the numerical value of 1 when expressed in terms of these units. Planck units elegantly simplify...
(c=1).
s is also known as the square of the center-of-mass energy (invariant mass
Invariant mass
The invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations...
) and t is also known as the square of the momentum transfer.
Feynman diagrams
The letters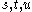 are also used in the terms s-channel, t-channel, u-channel. These channels represent different Feynman diagram
are also used in the terms s-channel, t-channel, u-channel. These channels represent different Feynman diagramFeynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s or different possible scattering events where the interaction involves the exchange of an intermediate particle whose squared four-momentum equals
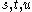 , respectively.
, respectively.-
- {|cellpadding="10"
|
|
|
|-
|align="center"|s-channel
|align="center"|t-channel
|align="center"|u-channel
|}
For example the s-channel corresponds to the particles 1,2 joining into an intermediate particle that eventually splits into 3,4: the s-channel is the only way that resonances and new unstable particles may be discovered provided their lifetimes are long enough that they are directly detectable. The t-channel represents the process in which the particle 1 emits the intermediate particle and becomes the final particle 3, while the particle 2 absorbs the intermediate particle and becomes 4. The u-channel is the t-channel with the role of the particles 3,4 interchanged.
The Mandelstam variables were first introduced by physicist Stanley Mandelstam
Stanley Mandelstam
Stanley Mandelstam is a South African-born theoretical physicist. He introduced the relativistically invariant Mandelstam variables into particle physics in 1958 as a convenient coordinate system for formulating his double dispersion relations...
in 1958.
High-energy limit
In the relativistic limit rest mass can be neglected, so for example,because
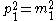 and
and 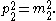 It is reminded that by relativistic limit one means that the momentum (speed) is so large that in the relativistic energy-momentum equation the energy becomes essentially the momentum norm (e.g.
It is reminded that by relativistic limit one means that the momentum (speed) is so large that in the relativistic energy-momentum equation the energy becomes essentially the momentum norm (e.g. 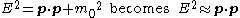 ).
).In summary,
|align="right"|
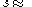
|align="right"|
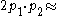
|align="right"|
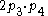
|-
|align="right"|
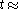
|
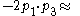
|
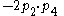
|-
|align="right"|
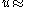
|
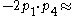
|
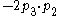
|}
Addition of
Note that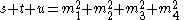
where
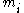 is the mass of particle
is the mass of particle  .
.Proof
To prove this, we need to use two facts:- The square of a particle's four momentum is the square of its mass,
-

- And conservation of four-momentum,


So, to begin,
First, use (1) to re-write these,
Then add them
|

|
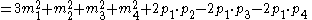
|-
|
|
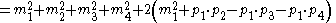
|-
|
|
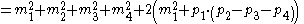
|}
Then use eq (2) to simplify further,
|
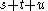
|
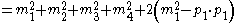
|-
|
|
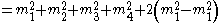
|}
So finally,
-
- {|cellpadding="2" style="border:2px solid #ccccff"
|
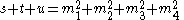
|}
See also
- Feynman diagrams
- Bhabha scatteringBhabha scatteringIn quantum electrodynamics, Bhabha scattering is the electron-positron scattering process:There are two leading-order Feynman diagrams contributing to this interaction: an annihilation process and a scattering process. The Bhabha scattering rate is used as a luminosity monitor in electron-positron...
- Møller scatteringMøller scatteringMøller scattering is the name given to electron-electron scattering in Quantum Field Theory. The electron interaction that is idealized in Møller scattering forms the theoretical basis of many familiar phenomena such as the repulsion of electrons in the Helium nucleus...
- Compton scatteringCompton scatteringIn physics, Compton scattering is a type of scattering that X-rays and gamma rays undergo in matter. The inelastic scattering of photons in matter results in a decrease in energy of an X-ray or gamma ray photon, called the Compton effect...