Binary cyclic group
Encyclopedia
In mathematics
, the binary cyclic group of the n-gon is the cyclic group of order 2n,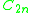
, thought of as an extension
of the cyclic group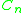
by a cyclic group
of order 2.
It is the binary polyhedral group corresponding to the cyclic group.
In terms of binary polyhedral groups, the binary cyclic group is the preimage of the cyclic group of rotations (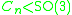
) under the 2:1 covering homomorphism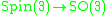
of the special orthogonal group by the spin group.
As a subgroup of the spin group, the binary cyclic group can be described concretely as a discrete subgroup of the unit quaternion
s, under the isomorphism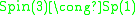
where Sp(1) is the multiplicative group of unit quaternions. (For a description of this homomorphism see the article on quaternions and spatial rotation
s.)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the binary cyclic group of the n-gon is the cyclic group of order 2n,
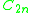, thought of as an extensionGroup extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence...
of the cyclic group
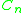by a cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order 2.
It is the binary polyhedral group corresponding to the cyclic group.
In terms of binary polyhedral groups, the binary cyclic group is the preimage of the cyclic group of rotations (
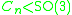) under the 2:1 covering homomorphism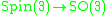of the special orthogonal group by the spin group.
As a subgroup of the spin group, the binary cyclic group can be described concretely as a discrete subgroup of the unit quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, under the isomorphism
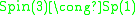where Sp(1) is the multiplicative group of unit quaternions. (For a description of this homomorphism see the article on quaternions and spatial rotationQuaternions and spatial rotation
Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
s.)
See also
- binary dihedral group
- binary tetrahedral group
- binary octahedral group
- binary icosahedral group