Binary tetrahedral group
Encyclopedia
In mathematics
, the binary tetrahedral group, denoted 2T or <2,3,3> is a certain nonabelian group
of order
24. It is an extension
of the tetrahedral group T or (2,3,3) of order 12 by a cyclic group
of order 2, and is the preimage of the tetrahedral group under the 2:1 covering homomorphism
of the special orthogonal group by the spin group. It follows that the binary octahedral group is a discrete subgroup of Spin(3) of order 24.
The binary tetrahedral group is most easily described concretely as a discrete subgroup of the unit quaternion
s, under the isomorphism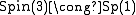
where Sp(1) is the multiplicative group of unit quaternions. (For a description of this homomorphism see the article on quaternions and spatial rotation
s.)
of Hurwitz integers. There are 24 such units given by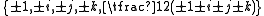
with all possible sign combinations.
All 24 units have absolute value 1 and therefore lie in the unit quaternion group Sp(1). The convex hull
of these 24 elements in 4-dimensional space form a convex regular 4-polytope
called the 24-cell.
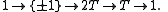
This sequence does not split, meaning that 2T is not a semidirect product
of {±1} by T. In fact, there is no subgroup of 2T isomorphic to T.
The binary tetrahedral group is the covering group
of the tetrahedral group. Thinking of the tetrahedral group as the alternating group on four letters,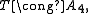
we thus have the binary tetrahedral group as the covering group,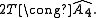 
The center of 2T is the subgroup {±1}, so that the inner automorphism group is isomorphic to T. The full automorphism group is isomorphic to S4 (the symmetric group
on 4 letters).
The binary tetrahedral group can be written as a semidirect product
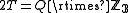
where Q is the quaternion group
consisting of the 8 Lipschitz units and Z3 is the cyclic group
of order 3 generated by ω = −½(1+i+j+k). The group Z3 acts on the normal subgroup Q by conjugation. Conjugation by ω is the automorphism of Q that cyclically rotates i, j, and k.
One can show that the binary tetrahedral group is isomorphic to the special linear group
SL(2,3) — the group of all 2×2 matrices over the finite field
F3 with unit determinant, with this isomorphism covering the isomorphism of the projective special linear group PSL(2,3) with the alternating group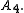
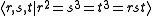
or equivalently,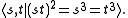
Generators with these relations are given by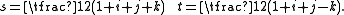
consisting of the 8 Lipschitz units forms a normal subgroup
of 2T of index 3. This group and the center {±1} are the only nontrivial normal subgroups.
All other subgroups of 2T are cyclic group
s generated by the various elements, with orders 3, 4, and 6.
(as a subgroup of SO(n)), there is a corresponding higher binary group which is a 2-fold cover, coming from the cover
The rotational symmetry group of the n-simplex can be considered as the alternating group on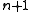
letters, 
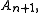and the corresponding binary group is a 2-fold covering group
. For all higher dimensions except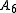
and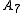 
(corresponding to the 5-dimensional and 6-dimensional simplexes), this binary group is the covering group (maximal cover) and is superperfect, but for dimensional 5 and 6 there is an additional exceptional 3-fold cover, and the binary groups are not superperfect.
It was first used in model building by Paul Frampton
and Thomas Kephart in 1994.
Evidence connecting models based on the binary tetrahedral group to the real world is a goal for the Large Hadron Collider
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the binary tetrahedral group, denoted 2T or <2,3,3> is a certain nonabelian group
Nonabelian group
In mathematics, a non-abelian group, also sometimes called a non-commutative group, is a group in which there are at least two elements a and b of G such that a * b ≠ b * a...
of order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
24. It is an extension
Group extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence...
of the tetrahedral group T or (2,3,3) of order 12 by a cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order 2, and is the preimage of the tetrahedral group under the 2:1 covering homomorphism
of the special orthogonal group by the spin group. It follows that the binary octahedral group is a discrete subgroup of Spin(3) of order 24.The binary tetrahedral group is most easily described concretely as a discrete subgroup of the unit quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, under the isomorphism
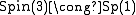where Sp(1) is the multiplicative group of unit quaternions. (For a description of this homomorphism see the article on quaternions and spatial rotationQuaternions and spatial rotation
Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
s.)
Elements
Explicitly, the binary tetrahedral group is given as the group of units in the ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of Hurwitz integers. There are 24 such units given by
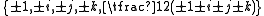
with all possible sign combinations.
All 24 units have absolute value 1 and therefore lie in the unit quaternion group Sp(1). The convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of these 24 elements in 4-dimensional space form a convex regular 4-polytope
Convex regular 4-polytope
In mathematics, a convex regular 4-polytope is a 4-dimensional polytope that is both regular and convex. These are the four-dimensional analogs of the Platonic solids and the regular polygons ....
called the 24-cell.
Properties
The binary tetrahedral group, denoted by 2T, fits into the short exact sequence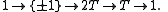This sequence does not split, meaning that 2T is not a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of {±1} by T. In fact, there is no subgroup of 2T isomorphic to T.
The binary tetrahedral group is the covering group
Covering groups of the alternating and symmetric groups
In the mathematical area of group theory, the covering groups of the alternating and symmetric groups are groups that are used to understand the projective representations of the alternating and symmetric groups...
of the tetrahedral group. Thinking of the tetrahedral group as the alternating group on four letters,
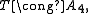we thus have the binary tetrahedral group as the covering group,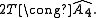 The center of 2T is the subgroup {±1}, so that the inner automorphism group is isomorphic to T. The full automorphism group is isomorphic to S4 (the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on 4 letters).
The binary tetrahedral group can be written as a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
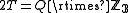
where Q is the quaternion group
Quaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
consisting of the 8 Lipschitz units and Z3 is the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order 3 generated by ω = −½(1+i+j+k). The group Z3 acts on the normal subgroup Q by conjugation. Conjugation by ω is the automorphism of Q that cyclically rotates i, j, and k.
One can show that the binary tetrahedral group is isomorphic to the special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
SL(2,3) — the group of all 2×2 matrices over the finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
F3 with unit determinant, with this isomorphism covering the isomorphism of the projective special linear group PSL(2,3) with the alternating group
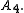
Presentation
The group 2T has a presentation given by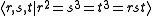or equivalently,
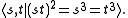
Generators with these relations are given by
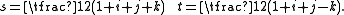
Subgroups
The quaternion groupQuaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
consisting of the 8 Lipschitz units forms a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of 2T of index 3. This group and the center {±1} are the only nontrivial normal subgroups.
All other subgroups of 2T are cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s generated by the various elements, with orders 3, 4, and 6.
Higher dimensions
Just as the tetrahedral group generalizes to the rotational symmetry group of the n-simplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
(as a subgroup of SO(n)), there is a corresponding higher binary group which is a 2-fold cover, coming from the cover
The rotational symmetry group of the n-simplex can be considered as the alternating group on
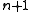letters, 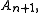and the corresponding binary group is a 2-fold covering groupCovering groups of the alternating and symmetric groups
In the mathematical area of group theory, the covering groups of the alternating and symmetric groups are groups that are used to understand the projective representations of the alternating and symmetric groups...
. For all higher dimensions except
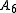and 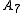(corresponding to the 5-dimensional and 6-dimensional simplexes), this binary group is the covering group (maximal cover) and is superperfect, but for dimensional 5 and 6 there is an additional exceptional 3-fold cover, and the binary groups are not superperfect.Usage in theoretical physics
The binary tetrahedral group was used in the context of Yang-Mills theory in 1956 by Chen Ning Yang.It was first used in model building by Paul Frampton
Paul Frampton
Paul Frampton is a particle phenomenologist.Since 1996, he is the Louis D. Rubin, Jr. Distinguished Professor of physics and astronomy, at the University of North Carolina...
and Thomas Kephart in 1994.
Evidence connecting models based on the binary tetrahedral group to the real world is a goal for the Large Hadron Collider
Large Hadron Collider
The Large Hadron Collider is the world's largest and highest-energy particle accelerator. It is expected to address some of the most fundamental questions of physics, advancing the understanding of the deepest laws of nature....
.
See also
- binary polyhedral group
- binary cyclic group
- binary dihedral group
- binary octahedral group
- binary icosahedral group