
Binary octahedral group
Encyclopedia
In mathematics
, the binary octahedral group, name as 2O or <2,3,4> is a certain nonabelian group
of order
48. It is an extension
of the octahedral group O or (2,3,4) of order 24 by a cyclic group
of order 2, and is the preimage of the octahedral group under the 2:1 covering homomorphism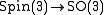 of the special orthogonal group by the spin group. It follows that the binary octahedral group is a discrete subgroup of Spin(3) of order 48.
of the special orthogonal group by the spin group. It follows that the binary octahedral group is a discrete subgroup of Spin(3) of order 48.
The binary octahedral group is most easily described concretely as a discrete subgroup of the unit quaternion
s, under the isomorphism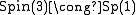 where Sp(1) is the multiplicative group of unit quaternions. (For a description of this homomorphism see the article on quaternions and spatial rotation
where Sp(1) is the multiplicative group of unit quaternions. (For a description of this homomorphism see the article on quaternions and spatial rotation
s.)

with all 24 quaternions obtained from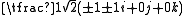
by a permutation
of coordinates (all possible sign combinations). All 48 elements have absolute value 1 and therefore lie in the unit quaternion group Sp(1).

This sequence does not split, meaning that 2O is not a semidirect product
of {±1} by O. In fact, there is no subgroup of 2O isomorphic to O.
The center of 2O is the subgroup {±1}, so that the inner automorphism group is isomorphic to O. The full automorphism group is isomorphic to O × Z2.

or equivalently,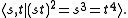
Generators with these relations are given by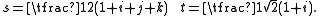
consisting of the 8 Lipschitz units forms a normal subgroup
of 2O of index 6. The quotient group
is isomorphic to S3 (the symmetric group
on 3 letters). The binary tetrahedral group, consisting of the 24 Hurwitz units, forms a normal subgroup of index 2. These two groups, together with the center {±1}, are the only nontrivial normal subgroups of 2O.
The generalized quaternion group of order 16 also forms a subgroup of 2O. This subgroup is self-normalizing so its conjugacy class
has 3 members. There are also isomorphic copies of the binary dihedral groups of orders 8 and 12 in 2O. All other subgroups are cyclic group
s generated by the various elements (with orders 3, 4, 6, and 8).
in SO(n), which has a binary cover under the map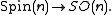
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the binary octahedral group, name as 2O or <2,3,4> is a certain nonabelian group
Nonabelian group
In mathematics, a non-abelian group, also sometimes called a non-commutative group, is a group in which there are at least two elements a and b of G such that a * b ≠ b * a...
of order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
48. It is an extension
Group extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence...
of the octahedral group O or (2,3,4) of order 24 by a cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order 2, and is the preimage of the octahedral group under the 2:1 covering homomorphism
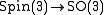 of the special orthogonal group by the spin group. It follows that the binary octahedral group is a discrete subgroup of Spin(3) of order 48.
of the special orthogonal group by the spin group. It follows that the binary octahedral group is a discrete subgroup of Spin(3) of order 48.The binary octahedral group is most easily described concretely as a discrete subgroup of the unit quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, under the isomorphism
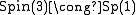 where Sp(1) is the multiplicative group of unit quaternions. (For a description of this homomorphism see the article on quaternions and spatial rotation
where Sp(1) is the multiplicative group of unit quaternions. (For a description of this homomorphism see the article on quaternions and spatial rotationQuaternions and spatial rotation
Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
s.)
Elements
Explicitly, the binary octahedral group is given as the union of the 24 Hurwitz units
with all 24 quaternions obtained from
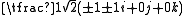
by a permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of coordinates (all possible sign combinations). All 48 elements have absolute value 1 and therefore lie in the unit quaternion group Sp(1).
Properties
The binary octahedral group, denoted by 2O, fits into the short exact sequence
This sequence does not split, meaning that 2O is not a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of {±1} by O. In fact, there is no subgroup of 2O isomorphic to O.
The center of 2O is the subgroup {±1}, so that the inner automorphism group is isomorphic to O. The full automorphism group is isomorphic to O × Z2.
Presentation
The group 2O has a presentation given by
or equivalently,
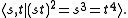
Generators with these relations are given by
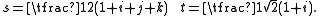
Subgroups
The quaternion groupQuaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
consisting of the 8 Lipschitz units forms a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of 2O of index 6. The quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
is isomorphic to S3 (the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on 3 letters). The binary tetrahedral group, consisting of the 24 Hurwitz units, forms a normal subgroup of index 2. These two groups, together with the center {±1}, are the only nontrivial normal subgroups of 2O.
The generalized quaternion group of order 16 also forms a subgroup of 2O. This subgroup is self-normalizing so its conjugacy class
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
has 3 members. There are also isomorphic copies of the binary dihedral groups of orders 8 and 12 in 2O. All other subgroups are cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s generated by the various elements (with orders 3, 4, 6, and 8).
Higher dimensions
The binary octahedral group generalizes to higher dimensions: just as the octahedron generalizes to the hyperoctahedron, the octahedral group in SO(3) generalizes to the hyperoctahedral groupHyperoctahedral group
In mathematics, a hyperoctahedral group is an important type of group that can be realized as the group of symmetries of a hypercube or of a cross-polytope. Groups of this type are identified by a parameter n, the dimension of the hypercube....
in SO(n), which has a binary cover under the map
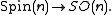
See also
- binary polyhedral group
- binary cyclic group
- binary dihedral group
- binary tetrahedral group
- binary icosahedral group
- hyperoctahedral groupHyperoctahedral groupIn mathematics, a hyperoctahedral group is an important type of group that can be realized as the group of symmetries of a hypercube or of a cross-polytope. Groups of this type are identified by a parameter n, the dimension of the hypercube....

