Quaternions and spatial rotation
Encyclopedia
Unit quaternions provide a convenient mathematical notation for representing orientation
s and rotation
s of objects in three dimensions. Compared to Euler angles
they are simpler to compose
and avoid the problem of gimbal lock
. Compared to rotation matrices they are more numerically stable and may be more efficient. Quaternions have found their way into applications in computer graphics
, computer vision
, robotics
, navigation
, molecular dynamics
and orbital mechanics of satellites.
When used to represent rotation, unit quaternions are also called versors, or rotation quaternions. When used to represent an orientation
(rotation relative to a reference position), they are called orientation quaternions or attitude quaternions.
of rotations in three dimensions in a very straightforward way. The correspondence between rotations and quaternions can be understood by first visualizing the space of rotations itself.
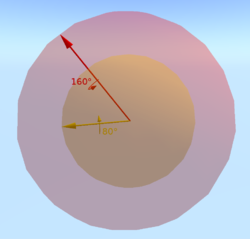In order to visualize the space of rotations, it helps to consider a simpler case. Any rotation in three dimensions can be described by a rotation by some angle about some axis. Consider the special case in which the axis of rotation lies in the xy plane. We can then specify the axis of one of these rotations by a point on a circle, and we can use the radius of the circle to specify the angle of rotation
. Similarly, a rotation whose axis of rotation lies in the "xy" plane can be described as a point on a sphere of fixed radius in three dimensions. Beginning at the north pole of a sphere in three dimensional space, we specify the point at the north pole to be the identity rotation (a zero angle rotation). Just as in the case of the identity rotation, no axis of rotation is defined, and the angle of rotation (zero) is irrelevant. A rotation having a very small rotation angle can be specified by a slice through the sphere parallel to the xy plane and very near the north pole. The circle defined by this slice will be very small, corresponding to the small angle of the rotation. As the rotation angles become larger, the slice moves in the negative "z" direction, and the circles become larger until the equator of the sphere is reached, which will correspond to a rotation angle of 180 degrees. Continuing southward, the radii of the circles now become smaller (corresponding to the absolute value of the angle of the rotation considered as a negative number). Finally, as the south pole is reached, the circles shrink once more to the identity rotation, which is also specified as the point at the south pole.
Notice that a number of characteristics of such rotations and their representations can be seen by this visualization. The space of rotations is continuous, each rotation has a neighborhood of rotations which are nearly the same, and this neighborhood becomes flat as the neighborhood shrinks. Also, each rotation is actually represented by two antipodal points on the sphere, which are at opposite ends of a line through the center of the sphere. This reflects the fact that each rotation can be represented as a rotation about some axis, or, equivalently, as a negative rotation about an axis pointing in the opposite direction (a so-called double cover). The "latitude" of a circle representing a particular rotation angle will be half of the angle represented by that rotation, since as the point is moved from the north to south pole, the latitude ranges from zero to 180 degrees, while the angle of rotation ranges from 0 to 360 degrees. (the "longitude" of a point then represents a particular axis of rotation.) Note however that this set of rotations is not closed under composition. Two successive rotations with axes in the xy plane will not necessarily give a rotation whose axis lies in the xy plane, and thus cannot be represented as a point on the sphere. This will not be the case with a general rotation in 3-space, in which rotations do form a closed set under composition.
This visualization can be extended to a general rotation in 3 dimensional space. The identity rotation is a point, and a small angle of rotation about some axis can be represented as a point on a sphere with a small radius. As the angle of rotation grows, the sphere grows, until the angle of rotation reaches 180 degrees, at which point the sphere begins to shrink, becoming a point as the angle approaches 360 degrees (or zero degrees from the negative direction). This set of expanding and contracting spheres represents a hypersphere in four dimensional space
(a 3-sphere). Just as in the simpler example above, each rotation represented as a point on the hypersphere is matched by its antipodal point on that hypersphere. The "latitude" on the hypersphere will be half of the corresponding angle of rotation, and the neighborhood of any point will become "flatter" (i.e. be represented by a 3-D Euclidean space of points) as the neighborhood shrinks. This behavior is matched by the set of unit quaternions: A general quaternion represents a point in a four dimensional space, but constraining it to have unit magnitude yields a three dimensional space equivalent to the surface of a hypersphere. The magnitude of the unit quaternion will be unity, corresponding to a hypersphere of unit radius. The vector part of a unit quaternion represents the radius of the 2-sphere corresponding to the axis of rotation, and its magnitude is the cosine of half the angle of rotation. Each rotation is represented by two unit quaternions of opposite sign, and, as in the space of rotations in three dimensions, the quaternion product of two unit quaternions will yield a unit quaternion. Also, the space of unit quaternions is "flat" in any infinitesimal neighborhood of a given unit quaternion.
) at the north and south poles, though the poles are not intrinsically different from any other points on the sphere. At the poles (latitudes +90° and -90°), the longitude becomes meaningless.
It can be shown that no two-parameter coordinate system can avoid such degeneracy. We can avoid such problems by embedding the sphere in three-dimensional space and parameterizing it with three Cartesian coordinates (here w,x,y), placing the north pole at (w,x,y) = (1,0,0), the south pole at (w,x,y) = (−1,0,0), and the equator at w = 0, x2 + y2 = 1. Points on the sphere satisfy the constraint w2 + x2 + y2 = 1, so we still have just two degrees of freedom
though there are three coordinates. A point (w,x,y) on the sphere represents a rotation in the ordinary space around the horizontal axis directed by the vector
by an angle 
.
In the same way the hyperspherical space of 3D rotations can be parameterized by three angles (Euler angles
), but any such parameterization is degenerate at some points on the hypersphere, leading to the problem of gimbal lock
. We can avoid this by using four Euclidean coordinates w,x,y,z, with w2 + x2 + y2 + z2 = 1. The point (w,x,y,z) represents a rotation around the axis directed by the vector
by an angle 
In the same way the quaternions can be defined by introducing abstract symbols i, j, k which satisfy the rules i2 = j2 = k2 = ijk = −1 and the usual algebraic rules except the commutative law of multiplication (a familiar example of such a noncommutative multiplication is matrix multiplication
). From this all of the rules of quaternion arithmetic follow: for example, one can show that:
The imaginary part
of a quaternion behaves like a vector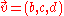 
in three dimension vector space, and the real part a behaves like a scalar
in
. When quaternions are used in geometry, it is more convenient to define them as a scalar plus a vector:
Those who have studied vectors at school might find it strange to add a number to a vector, as they are objects of very different natures, or to multiply two vectors together, as this operation is usually undefined. However, if one remembers that it is a mere notation for the real and imaginary parts of a quaternion, it becomes more legitimate. In other words, the correct reasoning is the addition of two quaternions, one with zero vector/imaginary part, and another one with zero scalar/real part:
We can express quaternion multiplication in the modern language of vector cross
and dot product
s (which were actually inspired by the quaternions in the first place ). In place of the rules i2 = j2 = k2 = ijk = −1 we have the quaternion multiplication rule:
where:
Quaternion multiplication is noncommutative (because of the cross product, which anti-commutes), while scalar-scalar and scalar-vector multiplications commute. From these rules it follows immediately that (see details):
The (left and right) multiplicative inverse or reciprocal of a nonzero quaternion is given by the conjugate-to-norm ratio (see details):
as can be verified by direct calculation.
around the axis 
as previously described. Define the quaternion
where
is a unit vector. Let also 
be an ordinary vector in 3 dimensional space, considered as a quaternion with a real coordinate equal to zero. Then it can be shown (see next section) that the quaternion product
yields the vector
upon rotation of the original vector 
by an angle 
around the axis 
. The rotation is clockwise if our line of sight points in the direction pointed by 
. This operation is known as conjugation by q.
It follows that quaternion multiplication is composition of rotations, for if p and q are quaternions representing rotations, then rotation (conjugation) by pq is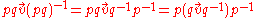
,
which is the same as rotating (conjugating) by q and then by p.
The quaternion inverse of a rotation is the opposite rotation, since
. The square of a quaternion rotation is a rotation by twice the angle around the same axis. More generally qn is a rotation by n times the angle around the same axis as q. This can be extended to arbitrary real n, allowing for smooth interpolation between spatial orientations; see Slerp
.
be a unit vector (the rotation axis) and let 
. Our goal is to show that
yields the vector
rotated by an angle 
around the axis 
. Expanding out, we have
where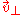
and 
are the components of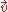 
perpendicular and parallel to 
respectively. This is the formula of a rotation
by
around the 
axis.
Consider the rotation f around the axis 
, with a rotation angle of 120°, or 2π⁄3 radian
s.
The length of
is √3, the half angle is π⁄3 (60°) with cosine ½, (cos 60° = 0.5) and sine
√3⁄2, (sin 60° ≈ 0.866). We are therefore dealing with a conjugation by the unit quaternion
If f is the rotation function,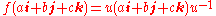
It can be proved that the inverse of a unit quaternion is obtained simply by changing the sign of its imaginary components. As a consequence,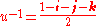
and
This can be simplified, using the ordinary rules for quaternion arithmetic, to
As expected, the rotation corresponds to keeping a cube
held fixed at one point, and rotating it 120° about the long diagonal through the fixed point (observe how the three axes are permuted cyclically
).
It gives us: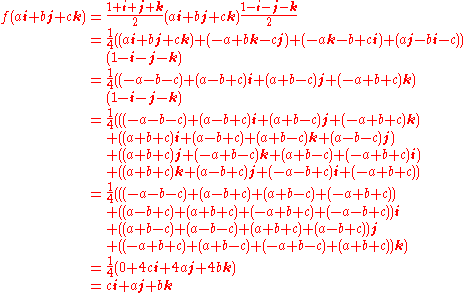
which is the expected result. As we can see, such computations are relatively long and tedious if done manually; however, in a computer program, this amounts to calling the quaternion multiplication routine twice.
Set two books next to each other. Rotate one of them 90 degrees clockwise around the z axis, then flip it 180 degrees around the x axis. Take the other book, flip it 180 around x axis first, and 90 clockwise around z later. The two books do not end up parallel. This shows that, in general, the composition of two different rotations around two distinct spatial axes will not commute.
Alternatively, if the quaternion or direction cosine matrix is interpreted as a rotation from one frame to another, then it must be either left-handed or right-handed. For example, in the above example rotating the X vector 90 degrees around the Z vector yields the Y vector only if you use the right hand rule. If you use a left hand rule, the result would be along the negative Y vector. Transformations from quaternion to direction cosine matrix often do not specify whether the input quaternion should be left handed or right handed. It is possible to determine the handedness of the algorithm by constructing a simple quaternion from a vector and an angle and assuming right handedness to begin with. For example, [0.7071, 0, 0, 0.7071 has the axis of rotation along the z-axis, and a rotation angle of 90 degrees. Pass this quaternion into the quaternion to matrix algorithm. If the end result is as shown below and you wish to interpret the matrix as right-handed, then the algorithm is expecting a right-handed quaternion. If the end result is the transpose and you still want to interpret the result as a right-handed matrix, then you must feed the algorithm left-handed quaternions. To convert between left and right-handed quaternions simply negate the vector part of the quaternion.
(9 numbers). Furthermore, for a given axis and angle, one can easily construct the corresponding quaternion, and conversely, for a given quaternion one can easily read off the axis and the angle. Both of these are much harder with matrices or Euler angles.
In computer games and other applications, one is often interested in “smooth rotations”, meaning that the scene should slowly rotate and not in a single step. This can be accomplished by choosing a curve
such as the spherical linear interpolation
in the quaternions, with one endpoint being the identity transformation 1 (or some other initial rotation) and the other being the intended final rotation. This is more problematic with other representations of rotations.
When composing several rotations on a computer, rounding errors necessarily accumulate. A quaternion that’s slightly off still represents a rotation after being normalised— a matrix that’s slightly off may not be orthogonal
anymore and is harder to convert back to a proper orthogonal matrix.
Quaternions also avoid a phenomenon called gimbal lock
which can result when, for example in pitch/yaw/roll rotational systems
, the pitch is rotated 90° up or down, so that yaw and roll then correspond to the same motion, and a degree of freedom of rotation is lost. In a gimbal
-based aerospace inertial navigation system, for instance, this could have disastrous results if the aircraft is in a steep dive or ascent.
corresponding to a rotation by the unit quaternion
(with |z| = 1) is given by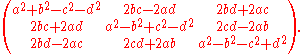
that corresponds to a rotation matrix 
can be numerically unstable if the trace
(sum of the diagonal elements) of the rotation matrix is zero or very small. A robust method is to choose the diagonal element
with the largest value. Let uvw be an even permutation of xyz (i.e. xyz, yzx or zxy). The value
will be a real number because
. If r is zero the matrix is the identity matrix, and the quaternion must be the identity quaternion (1, 0, 0, 0). Otherwise the quaternion can be calculated as follows:
Beware the vector convention: There are two conventions for rotation matrices: one assumes row vectors on the left; the other assumes column vectors on the right; the two conventions generate matrices that are the transpose of each other. The above matrix assumes column vectors on the right. In general, a matrix for vertex transpose is ambiguous unless the vector convention is also mentioned. Historically, the column-on-the-right convention comes from mathematics and classical mechanics, whereas row-vector-on-the-left comes from computer graphics, where typesetting row vectors was easier back in the early days.
(Compare the equivalent general formula for a 3 × 3 rotation matrix in terms of the axis and the angle.)
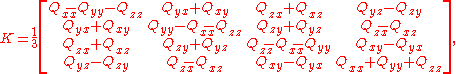
and find the eigenvector (x,y,z,w) corresponding to the largest eigenvalue (that value will be 1 if and only if Q is a pure rotation). The quaternion so obtained will correspond to the rotation closest to the original matrix Q
* Note: angle-axis can be stored as 3 elements by multiplying the unit rotation axis by the rotation angle, forming the logarithm of the quaternion, at the cost of additional calculations.
:
, and pretending that it is a quaternion, we can rotate the vector 
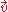like this:
It is straightforward to check that for each matrix M MT = I, that is, that each matrix (and hence both matrices together) represents a rotation. Note that since
, the two matrices must commute. Therefore, there are two commuting subgroups of the set of four dimensional rotations. Arbitrary four dimensional rotations have 6 degrees of freedom, each matrix represents 3 of those 6 degrees of freedom.
Since an infinitesimal
four-dimensional rotation can be represented by a pair of quaternions (as follows), all (non-infinitesimal) four-dimensional rotations can also be represented.
Orientation (geometry)
In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
s and rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s of objects in three dimensions. Compared to Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
they are simpler to compose
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
and avoid the problem of gimbal lock
Gimbal lock
Gimbal lock is the loss of one degree of freedom in a three-dimensional space that occurs when the axes of two of the three gimbals are driven into a parallel configuration, "locking" the system into rotation in a degenerate two-dimensional space....
. Compared to rotation matrices they are more numerically stable and may be more efficient. Quaternions have found their way into applications in computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, robotics
Robotics
Robotics is the branch of technology that deals with the design, construction, operation, structural disposition, manufacture and application of robots...
, navigation
Navigation
Navigation is the process of monitoring and controlling the movement of a craft or vehicle from one place to another. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks...
, molecular dynamics
Molecular dynamics
Molecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
and orbital mechanics of satellites.
When used to represent rotation, unit quaternions are also called versors, or rotation quaternions. When used to represent an orientation
Orientation (geometry)
In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
(rotation relative to a reference position), they are called orientation quaternions or attitude quaternions.
Quaternion rotation operations
A very formal explanation of the properties used in this section is given by Altmann.Visualizing the space of rotations
Unit quaternions represent the mathematical spaceMathematical space
In mathematics, a space is a set with some added structure.Mathematical spaces often form a hierarchy, i.e., one space may inherit all the characteristics of a parent space...
of rotations in three dimensions in a very straightforward way. The correspondence between rotations and quaternions can be understood by first visualizing the space of rotations itself.
Angle of rotation
In mathematics, the angle of rotation is a measurement of the amount, the angle, that a figure is rotated about a fixed point, often the center of a circle....
. Similarly, a rotation whose axis of rotation lies in the "xy" plane can be described as a point on a sphere of fixed radius in three dimensions. Beginning at the north pole of a sphere in three dimensional space, we specify the point at the north pole to be the identity rotation (a zero angle rotation). Just as in the case of the identity rotation, no axis of rotation is defined, and the angle of rotation (zero) is irrelevant. A rotation having a very small rotation angle can be specified by a slice through the sphere parallel to the xy plane and very near the north pole. The circle defined by this slice will be very small, corresponding to the small angle of the rotation. As the rotation angles become larger, the slice moves in the negative "z" direction, and the circles become larger until the equator of the sphere is reached, which will correspond to a rotation angle of 180 degrees. Continuing southward, the radii of the circles now become smaller (corresponding to the absolute value of the angle of the rotation considered as a negative number). Finally, as the south pole is reached, the circles shrink once more to the identity rotation, which is also specified as the point at the south pole.
Notice that a number of characteristics of such rotations and their representations can be seen by this visualization. The space of rotations is continuous, each rotation has a neighborhood of rotations which are nearly the same, and this neighborhood becomes flat as the neighborhood shrinks. Also, each rotation is actually represented by two antipodal points on the sphere, which are at opposite ends of a line through the center of the sphere. This reflects the fact that each rotation can be represented as a rotation about some axis, or, equivalently, as a negative rotation about an axis pointing in the opposite direction (a so-called double cover). The "latitude" of a circle representing a particular rotation angle will be half of the angle represented by that rotation, since as the point is moved from the north to south pole, the latitude ranges from zero to 180 degrees, while the angle of rotation ranges from 0 to 360 degrees. (the "longitude" of a point then represents a particular axis of rotation.) Note however that this set of rotations is not closed under composition. Two successive rotations with axes in the xy plane will not necessarily give a rotation whose axis lies in the xy plane, and thus cannot be represented as a point on the sphere. This will not be the case with a general rotation in 3-space, in which rotations do form a closed set under composition.
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
(a 3-sphere). Just as in the simpler example above, each rotation represented as a point on the hypersphere is matched by its antipodal point on that hypersphere. The "latitude" on the hypersphere will be half of the corresponding angle of rotation, and the neighborhood of any point will become "flatter" (i.e. be represented by a 3-D Euclidean space of points) as the neighborhood shrinks. This behavior is matched by the set of unit quaternions: A general quaternion represents a point in a four dimensional space, but constraining it to have unit magnitude yields a three dimensional space equivalent to the surface of a hypersphere. The magnitude of the unit quaternion will be unity, corresponding to a hypersphere of unit radius. The vector part of a unit quaternion represents the radius of the 2-sphere corresponding to the axis of rotation, and its magnitude is the cosine of half the angle of rotation. Each rotation is represented by two unit quaternions of opposite sign, and, as in the space of rotations in three dimensions, the quaternion product of two unit quaternions will yield a unit quaternion. Also, the space of unit quaternions is "flat" in any infinitesimal neighborhood of a given unit quaternion.
Parameterizing the space of rotations
We can parameterize the surface of a sphere with two coordinates, such as latitude and longitude. But latitude and longitude are ill-behaved (degenerateDegeneracy (mathematics)
In mathematics, a degenerate case is a limiting case in which a class of object changes its nature so as to belong to another, usually simpler, class....
) at the north and south poles, though the poles are not intrinsically different from any other points on the sphere. At the poles (latitudes +90° and -90°), the longitude becomes meaningless.
It can be shown that no two-parameter coordinate system can avoid such degeneracy. We can avoid such problems by embedding the sphere in three-dimensional space and parameterizing it with three Cartesian coordinates (here w,x,y), placing the north pole at (w,x,y) = (1,0,0), the south pole at (w,x,y) = (−1,0,0), and the equator at w = 0, x2 + y2 = 1. Points on the sphere satisfy the constraint w2 + x2 + y2 = 1, so we still have just two degrees of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
though there are three coordinates. A point (w,x,y) on the sphere represents a rotation in the ordinary space around the horizontal axis directed by the vector
by an angle .In the same way the hyperspherical space of 3D rotations can be parameterized by three angles (Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
), but any such parameterization is degenerate at some points on the hypersphere, leading to the problem of gimbal lock
Gimbal lock
Gimbal lock is the loss of one degree of freedom in a three-dimensional space that occurs when the axes of two of the three gimbals are driven into a parallel configuration, "locking" the system into rotation in a degenerate two-dimensional space....
. We can avoid this by using four Euclidean coordinates w,x,y,z, with w2 + x2 + y2 + z2 = 1. The point (w,x,y,z) represents a rotation around the axis directed by the vector
by an angle Quaternions briefly
The complex numbers can be defined by introducing an abstract symbol i which satisfies the usual rules of algebra and additionally the rule i2 = −1. This is sufficient to reproduce all of the rules of complex number arithmetic: for example:-
.
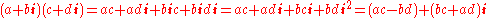In the same way the quaternions can be defined by introducing abstract symbols i, j, k which satisfy the rules i2 = j2 = k2 = ijk = −1 and the usual algebraic rules except the commutative law of multiplication (a familiar example of such a noncommutative multiplication is matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
). From this all of the rules of quaternion arithmetic follow: for example, one can show that:
-
.
The imaginary part
of a quaternion behaves like a vector 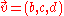in three dimension vector space, and the real part a behaves like a scalarScalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
in
. When quaternions are used in geometry, it is more convenient to define them as a scalar plus a vector:
-
.
Those who have studied vectors at school might find it strange to add a number to a vector, as they are objects of very different natures, or to multiply two vectors together, as this operation is usually undefined. However, if one remembers that it is a mere notation for the real and imaginary parts of a quaternion, it becomes more legitimate. In other words, the correct reasoning is the addition of two quaternions, one with zero vector/imaginary part, and another one with zero scalar/real part:
-
.
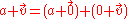We can express quaternion multiplication in the modern language of vector cross
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
and dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
s (which were actually inspired by the quaternions in the first place ). In place of the rules i2 = j2 = k2 = ijk = −1 we have the quaternion multiplication rule:
where:
-
is the resulting quaternion, -
is vector cross product (a vector), -
is vector scalar product (a scalar).
Quaternion multiplication is noncommutative (because of the cross product, which anti-commutes), while scalar-scalar and scalar-vector multiplications commute. From these rules it follows immediately that (see details):
-
.
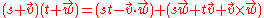The (left and right) multiplicative inverse or reciprocal of a nonzero quaternion is given by the conjugate-to-norm ratio (see details):
-
,
as can be verified by direct calculation.
Describing rotations with quaternions
Let (w,x,y,z) be the coordinates of a rotation by around the axis as previously described. Define the quaternionwhere
is a unit vector. Let also be an ordinary vector in 3 dimensional space, considered as a quaternion with a real coordinate equal to zero. Then it can be shown (see next section) that the quaternion productyields the vector
upon rotation of the original vector by an angle around the axis . The rotation is clockwise if our line of sight points in the direction pointed by . This operation is known as conjugation by q.It follows that quaternion multiplication is composition of rotations, for if p and q are quaternions representing rotations, then rotation (conjugation) by pq is
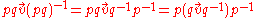,which is the same as rotating (conjugating) by q and then by p.
The quaternion inverse of a rotation is the opposite rotation, since
. The square of a quaternion rotation is a rotation by twice the angle around the same axis. More generally qn is a rotation by n times the angle around the same axis as q. This can be extended to arbitrary real n, allowing for smooth interpolation between spatial orientations; see SlerpSlerp
In computer graphics, Slerp is shorthand for spherical linear interpolation, introduced by Ken Shoemake in the context of quaternion interpolation for the purpose of animating 3D rotation...
.
Proof of the quaternion rotation identity
Let be a unit vector (the rotation axis) and let . Our goal is to show thatyields the vector
rotated by an angle around the axis . Expanding out, we havewhere
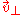and are the components of 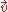perpendicular and parallel to respectively. This is the formula of a rotationRodrigues' rotation formula
In the theory of three-dimensional rotation, Rodrigues' rotation formula is an efficient algorithm for rotating a vector in space, given an axis and angle of rotation. By extension, this can be used to transform all three basis vectors to compute a rotation matrix from an axis-angle representation...
by
around the axis.The conjugation operation
, with a rotation angle of 120°, or 2π⁄3 radianRadian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s.
The length of
is √3, the half angle is π⁄3 (60°) with cosine ½, (cos 60° = 0.5) and sineSine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
√3⁄2, (sin 60° ≈ 0.866). We are therefore dealing with a conjugation by the unit quaternion
If f is the rotation function,
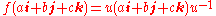
It can be proved that the inverse of a unit quaternion is obtained simply by changing the sign of its imaginary components. As a consequence,
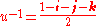
and
This can be simplified, using the ordinary rules for quaternion arithmetic, to
As expected, the rotation corresponds to keeping a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
held fixed at one point, and rotating it 120° about the long diagonal through the fixed point (observe how the three axes are permuted cyclically
Cyclic permutation
A cyclic permutation or circular permutation is a permutation built from one or more sets of elements in cyclic order.The notion "cyclic permutation" is used in different, but related ways:- Definition 1 :right|mapping of permutation...
).
Quaternion arithmetic in practice
Let's show how we reached the previous result. Let's develop the expression of f (in two stages), and apply the rulesIt gives us:
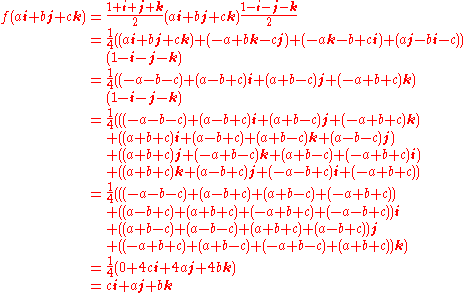
which is the expected result. As we can see, such computations are relatively long and tedious if done manually; however, in a computer program, this amounts to calling the quaternion multiplication routine twice.
Non-commutativity
The multiplication of quaternions is non-commutative. Since the multiplication of unit quaternions corresponds to the composition of three dimensional rotations, this property can be made intuitive by showing that three dimensional rotations are not commutative in general.Set two books next to each other. Rotate one of them 90 degrees clockwise around the z axis, then flip it 180 degrees around the x axis. Take the other book, flip it 180 around x axis first, and 90 clockwise around z later. The two books do not end up parallel. This shows that, in general, the composition of two different rotations around two distinct spatial axes will not commute.
Are quaternions handed?
Note that quaternions, like the rotations or other linear transforms, are not "handed" (as in left-handed vs right-handed). Handedness of a coordinate system comes from the interpretation of the numbers in physical space. No matter what the handedness convention, rotating the X vector 90 degrees around the Z vector will yield the Y vector — the mathematics and numbers are the same.Alternatively, if the quaternion or direction cosine matrix is interpreted as a rotation from one frame to another, then it must be either left-handed or right-handed. For example, in the above example rotating the X vector 90 degrees around the Z vector yields the Y vector only if you use the right hand rule. If you use a left hand rule, the result would be along the negative Y vector. Transformations from quaternion to direction cosine matrix often do not specify whether the input quaternion should be left handed or right handed. It is possible to determine the handedness of the algorithm by constructing a simple quaternion from a vector and an angle and assuming right handedness to begin with. For example, [0.7071, 0, 0, 0.7071 has the axis of rotation along the z-axis, and a rotation angle of 90 degrees. Pass this quaternion into the quaternion to matrix algorithm. If the end result is as shown below and you wish to interpret the matrix as right-handed, then the algorithm is expecting a right-handed quaternion. If the end result is the transpose and you still want to interpret the result as a right-handed matrix, then you must feed the algorithm left-handed quaternions. To convert between left and right-handed quaternions simply negate the vector part of the quaternion.
Qualitative description of the advantages of quaternions
The representation of a rotation as a quaternion (4 numbers) is more compact than the representation as an orthogonal matrixOrthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
(9 numbers). Furthermore, for a given axis and angle, one can easily construct the corresponding quaternion, and conversely, for a given quaternion one can easily read off the axis and the angle. Both of these are much harder with matrices or Euler angles.
In computer games and other applications, one is often interested in “smooth rotations”, meaning that the scene should slowly rotate and not in a single step. This can be accomplished by choosing a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
such as the spherical linear interpolation
Slerp
In computer graphics, Slerp is shorthand for spherical linear interpolation, introduced by Ken Shoemake in the context of quaternion interpolation for the purpose of animating 3D rotation...
in the quaternions, with one endpoint being the identity transformation 1 (or some other initial rotation) and the other being the intended final rotation. This is more problematic with other representations of rotations.
When composing several rotations on a computer, rounding errors necessarily accumulate. A quaternion that’s slightly off still represents a rotation after being normalised— a matrix that’s slightly off may not be orthogonal
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
anymore and is harder to convert back to a proper orthogonal matrix.
Quaternions also avoid a phenomenon called gimbal lock
Gimbal lock
Gimbal lock is the loss of one degree of freedom in a three-dimensional space that occurs when the axes of two of the three gimbals are driven into a parallel configuration, "locking" the system into rotation in a degenerate two-dimensional space....
which can result when, for example in pitch/yaw/roll rotational systems
Flight dynamics
Flight dynamics is the science of air vehicle orientation and control in three dimensions. The three critical flight dynamics parameters are the angles of rotation in three dimensions about the vehicle's center of mass, known as pitch, roll and yaw .Aerospace engineers develop control systems for...
, the pitch is rotated 90° up or down, so that yaw and roll then correspond to the same motion, and a degree of freedom of rotation is lost. In a gimbal
Gimbal
A gimbal is a pivoted support that allows the rotation of an object about a single axis. A set of two gimbals, one mounted on the other with pivot axes orthogonal, may be used to allow an object mounted on the innermost gimbal to remain immobile regardless of the motion of its support...
-based aerospace inertial navigation system, for instance, this could have disastrous results if the aircraft is in a steep dive or ascent.
From a quaternion to an orthogonal matrix
The orthogonal matrixOrthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
corresponding to a rotation by the unit quaternion
(with |z| = 1) is given by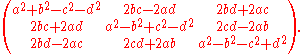From an orthogonal matrix to a quaternion
Finding the quaternion that corresponds to a rotation matrix can be numerically unstable if the traceTrace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
(sum of the diagonal elements) of the rotation matrix is zero or very small. A robust method is to choose the diagonal element
with the largest value. Let uvw be an even permutation of xyz (i.e. xyz, yzx or zxy). The valuewill be a real number because
. If r is zero the matrix is the identity matrix, and the quaternion must be the identity quaternion (1, 0, 0, 0). Otherwise the quaternion can be calculated as follows: Beware the vector convention: There are two conventions for rotation matrices: one assumes row vectors on the left; the other assumes column vectors on the right; the two conventions generate matrices that are the transpose of each other. The above matrix assumes column vectors on the right. In general, a matrix for vertex transpose is ambiguous unless the vector convention is also mentioned. Historically, the column-on-the-right convention comes from mathematics and classical mechanics, whereas row-vector-on-the-left comes from computer graphics, where typesetting row vectors was easier back in the early days.
(Compare the equivalent general formula for a 3 × 3 rotation matrix in terms of the axis and the angle.)
Fitting quaternions
The above section described how to recover a quaternion q from a 3 × 3 rotation matrix Q. Suppose, however, that we have some matrix Q that is not a pure rotation — due to round-off errors, for example — and we wish to find the quaternion q that most accurately represents Q. In that case we construct a symmetric 4×4 matrix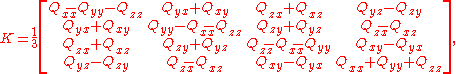and find the eigenvector (x,y,z,w) corresponding to the largest eigenvalue (that value will be 1 if and only if Q is a pure rotation). The quaternion so obtained will correspond to the rotation closest to the original matrix Q
Performance comparisons with other rotation methods
This section discusses the performance implications of using quaternions versus other methods (axis/angle or rotation matrices) to perform rotations in 3D.Results
| Method | Storage |
|---|---|
| Rotation matrix | 9 |
| Quaternion Quaternion In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space... |
4 |
| Angle/axis | 3* |
| Method | # multiplies | # add/subtracts | total operations |
|---|---|---|---|
| Rotation matrices | 27 | 18 | 45 |
| Quaternions | 16 | 12 | 28 |
| Method | # multiplies | # add/subtracts | # sin/cos | total operations |
|---|---|---|---|---|
| Rotation matrix | 9 | 6 | 0 | 15 |
| Quaternions | 18 | 12 | 0 | 30 |
| Angle/axis | 23 | 16 | 2 | 41 |
Used methods
There are three basic approaches to rotating a vector:
- Compute the matrix product of a 3x3 rotation matrix R and the original 3x1 column matrix representing
. This requires 3*(3 multiplications + 2 additions) = 9 multiplications and 6 additions, the most efficient method for rotating a vector. - Using the quaternion-vector rotation formula derived above of
, the rotated vector can be evaluated directly via two quaternion products from the definition. However, the number of multiply/add operations can be minimised by expanding both quaternion products of 
into vector operations by twice applying 
. Further applying a number of vector identities yields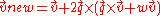 
which requires only 18 multiplies and 12 additions to evaluate. As a second approach, the quaternion could first be converted to its equivalent angle/axis representation then the angle/axis representation used to rotate the vector. However, this is both less efficient and less numerically stable when the quaternion nears the no-rotation point. - Use the angle-axis formula to convert an angle/axis to a rotation matrix R then multiplying with a vector. Converting the angle/axis to R using common subexpression eliminationCommon subexpression eliminationIn computer science, common subexpression elimination is a compiler optimization that searches for instances of identical expressions , and analyses whether it is worthwhile replacing them with a single variable holding the computed value.- Example :In the following code: a = b * c + g; d = b * c...
costs 14 multiplies, 2 function calls (sin, cos), and 10 add/subtracts; from item 1, rotating using R adds an additional 9 multiplications and 6 additions for a total of 23 multiplies, 16 add/subtracts, and 2 function calls (sin, cos).
Pairs of unit quaternions as rotations in 4D space
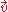A pair of unit quaternions zl and zr can represent any rotation in 4D space. Given a four dimensional vector, and pretending that it is a quaternion, we can rotate the vector like this:It is straightforward to check that for each matrix M MT = I, that is, that each matrix (and hence both matrices together) represents a rotation. Note that since
, the two matrices must commute. Therefore, there are two commuting subgroups of the set of four dimensional rotations. Arbitrary four dimensional rotations have 6 degrees of freedom, each matrix represents 3 of those 6 degrees of freedom.Since an infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
four-dimensional rotation can be represented by a pair of quaternions (as follows), all (non-infinitesimal) four-dimensional rotations can also be represented.
See also
- 3-sphere3-sphereIn mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
- Axis angleAxis angleThe axis-angle representation of a rotation, also known as the exponential coordinates of a rotation, parameterizes a rotation by two values: a unit vector indicating the direction of a directed axis , and an angle describing the magnitude of the rotation about the axis...
- Simultaneous orthogonal rotations angleSimultaneous orthogonal rotations angleA simultaneous orthogonal rotations angle is a vector representing angular orientation of a rigid-body relative to some reference frame...
- Biquaternion
- Charts on SO(3)Charts on SO(3)In mathematics, the special orthogonal group in three dimensions, otherwise known as the rotation group SO, is a naturally occurring example of a manifold. The various charts on SO set up rival coordinate systems: in this case there cannot be said to be a preferred set of parameters describing a...
- Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
s - Coordinate rotations
- Conversion between quaternions and Euler anglesConversion between quaternions and Euler anglesSpatial rotations in three dimensions can be parametrized using both Euler angles and unit quaternions. This article explains how to convert between the two representations. Actually this simple use of "quaternions" was first presented by Euler some seventy years earlier than Hamilton to solve the...
- Covering mapCovering mapIn mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
- Dual quaternionDual quaternionThe set of dual quaternions is an algebra that can be used to represent spatial rigid body displacements. A dual quaternion is an ordered pair of quaternions  = and therefore is constructed from eight real parameters. Because rigid body displacements are defined by six parameters, dual...
- Elliptic geometry#Elliptic space
- Rotation representation (mathematics)Rotation representation (mathematics)In geometry a rotation representation expresses a rotation as a mathematical transformation. In physics, this concept extends to classical mechanics where rotational kinematics is the science of describing with numbers the purely rotational motion of an object.According to Euler's rotation theorem...
- Rotation groupRotation groupIn mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
- SO(4)SO(4)In mathematics, the group of rotations about a fixed point in four-dimensional Euclidean space is denoted SO. The name comes from the fact that it is the special orthogonal group of order 4....
- Spinor group
- SlerpSlerpIn computer graphics, Slerp is shorthand for spherical linear interpolation, introduced by Ken Shoemake in the context of quaternion interpolation for the purpose of animating 3D rotation...
— spherical linear interpolation
- Olinde RodriguesOlinde RodriguesBenjamin Olinde Rodrigues , more commonly known as Olinde Rodrigues, was a French banker, mathematician, and social reformer.Rodrigues was born into a well-to-do Sephardi Jewish family in Bordeaux....
- William Rowan HamiltonWilliam Rowan HamiltonSir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
External links and resources
- Shoemake, Ken. Quaternions
- Simple Quaternion type and operations in more than twenty different languages on Rosetta CodeRosetta CodeRosetta Code is a wiki-based programming chrestomathy website with solutions to various programming problems in many different programming languages. It was created in 2007 by Mike Mol. Rosetta Code includes 450 programming tasks, and covers 351 programming languages...
- Hart, Francis, Kauffman. Quaternion demo
- Dam, Koch, Lillholm. Quaternions, Interpolation and Animation
- Byung-Uk Lee. Unit Quaternion Representation of Rotation
- Ibanez, Luis. Quaternion Tutorial I
- Ibanez, Luis. Quaternion Tutorial II
- [ftp://ftp.cs.unc.edu/pub/techreports/01-014.pdf Vicci, Leandra. Quaternions and Rotations in 3-Space: The Algebra and its Geometric Interpretation]
- Howell, Thomas and Lafon, Jean-Claude. The Complexity of the Quaternion Product, TR75-245, Cornell University, 1975
- Berthold K.P. Horn. Some Notes on Unit Quaternions and Rotation.