Slerp
Encyclopedia
In computer graphics
, Slerp is shorthand for spherical linear interpolation, introduced by Ken Shoemake in the context of quaternion
interpolation
for the purpose of animating
3D rotation
. It refers to constant-speed motion along a unit-radius great circle
arc, given the ends and an interpolation parameter between 0 and 1.
of the ends. Let p0 and p1 be the first and last points of the arc, and let t be the parameter, 0 ≤ t ≤ 1. Compute Ω as the angle subtended by the arc, so that , the n-dimensional dot product
of the unit vectors from the origin to the ends. The geometric formula is then
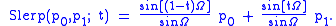
The symmetry can be seen in the fact that = . In the limit as Ω → 0, this formula reduces to the corresponding symmetric formula for linear interpolation
,
A Slerp path is, in fact, the spherical geometry equivalent of a path along a line segment in the plane; a great circle is a spherical geodesic
.
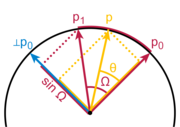More familiar than the general Slerp formula is the case when the end vectors are perpendicular, in which case the formula is . Letting , and applying the trigonometric identity , this becomes the Slerp formula. The factor of in the general formula is a normalization, since a vector p1 at an angle of Ω to p0 projects onto the perpendicular ⊥p0 with a length of only .
Some special cases of Slerp admit more efficient calculation. When a circular arc is to be drawn into a raster image, the preferred method is some variation of Bresenham's
circle algorithm. Evaluation at the special parameter values 0 and 1 trivially yields p0 and p1, respectively; and bisection, evaluation at ½, simplifies to , normalized. Another special case, common in animation, is evaluation with fixed ends and equal parametric steps. If pk−1 and pk are two consecutive values, and if c is twice their dot product (constant for all steps), then the next value, pk+1, is the reflection .
s, the quaternion path maps to a path through 3D rotations in a standard way
. The effect is a rotation with uniform angular velocity
around a fixed rotation axis. When the initial end point is the identity quaternion, Slerp gives a segment of a one-parameter subgroup of both the Lie group
of 3D rotations, SO(3), and its universal covering group
of unit quaternions, S3
. Slerp gives a straightest and shortest path between its quaternion end points, and maps to a rotation through an angle of 2Ω. However, because the covering is double (q and −q map to the same rotation), the rotation path may turn either the "short way" (less than 180°) or the "long way" (more than 180°). Long paths can be prevented by negating one end if the dot product, , is negative, thus ensuring that −90° ≤ Ω ≤ 90°.
Slerp also has expressions in terms of quaternion algebra, all using exponentiation
. Real powers of a quaternion are defined in terms of the quaternion exponential function
, written as and given by the power series equally familiar from calculus, complex analysis and matrix algebra:
Writing a unit quaternion q in versor form, , with v a unit 3-vector, and noting that the quaternion square v2 equals −1 (implying a quaternion version of Euler's formula
), we have , and . The identification of interest is , so that the real part of q is , the same as the geometric dot product used above. Here are four equivalent quaternion expressions for Slerp.
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, Slerp is shorthand for spherical linear interpolation, introduced by Ken Shoemake in the context of quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
interpolation
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
for the purpose of animating
Animation
Animation is the rapid display of a sequence of images of 2-D or 3-D artwork or model positions in order to create an illusion of movement. The effect is an optical illusion of motion due to the phenomenon of persistence of vision, and can be created and demonstrated in several ways...
3D rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
. It refers to constant-speed motion along a unit-radius great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
arc, given the ends and an interpolation parameter between 0 and 1.
Geometric Slerp
Slerp has a geometric formula independent of quaternions, and independent of the dimension of the space in which the arc is embedded. This formula, a symmetric weighted sum credited to Glenn Davis, is based on the fact that any point on the curve must be a linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the ends. Let p0 and p1 be the first and last points of the arc, and let t be the parameter, 0 ≤ t ≤ 1. Compute Ω as the angle subtended by the arc, so that , the n-dimensional dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of the unit vectors from the origin to the ends. The geometric formula is then
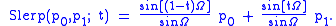
The symmetry can be seen in the fact that = . In the limit as Ω → 0, this formula reduces to the corresponding symmetric formula for linear interpolation
Linear interpolation
Linear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...
,
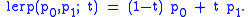
A Slerp path is, in fact, the spherical geometry equivalent of a path along a line segment in the plane; a great circle is a spherical geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
.
Some special cases of Slerp admit more efficient calculation. When a circular arc is to be drawn into a raster image, the preferred method is some variation of Bresenham's
Jack E. Bresenham
Jack Elton Bresenham is a former professor of computer science.-Biography:He retired from 27 years of service at IBM as a Senior Technical Staff Member in 1987. He taught for 16 years at Winthrop University and has nine patents...
circle algorithm. Evaluation at the special parameter values 0 and 1 trivially yields p0 and p1, respectively; and bisection, evaluation at ½, simplifies to , normalized. Another special case, common in animation, is evaluation with fixed ends and equal parametric steps. If pk−1 and pk are two consecutive values, and if c is twice their dot product (constant for all steps), then the next value, pk+1, is the reflection .
Quaternion Slerp
When Slerp is applied to unit quaternionQuaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, the quaternion path maps to a path through 3D rotations in a standard way
Quaternions and spatial rotation
Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
. The effect is a rotation with uniform angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
around a fixed rotation axis. When the initial end point is the identity quaternion, Slerp gives a segment of a one-parameter subgroup of both the Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
of 3D rotations, SO(3), and its universal covering group
Covering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
of unit quaternions, S3
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
. Slerp gives a straightest and shortest path between its quaternion end points, and maps to a rotation through an angle of 2Ω. However, because the covering is double (q and −q map to the same rotation), the rotation path may turn either the "short way" (less than 180°) or the "long way" (more than 180°). Long paths can be prevented by negating one end if the dot product, , is negative, thus ensuring that −90° ≤ Ω ≤ 90°.
Slerp also has expressions in terms of quaternion algebra, all using exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
. Real powers of a quaternion are defined in terms of the quaternion exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
, written as and given by the power series equally familiar from calculus, complex analysis and matrix algebra:
Writing a unit quaternion q in versor form, , with v a unit 3-vector, and noting that the quaternion square v2 equals −1 (implying a quaternion version of Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
), we have , and . The identification of interest is , so that the real part of q is , the same as the geometric dot product used above. Here are four equivalent quaternion expressions for Slerp.
-
The derivativeDerivativeIn calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of with respect to t, assuming the ends are fixed, is log(q1q0−1) times the function value, where the quaternion natural logarithmNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
in this case yields half the 3D angular velocityAngular velocityIn physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
vector. The initial tangent vector is parallel transportParallel transportIn geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
ed to each tangent along the curve; thus the curve is, indeed, a geodesic.
In the tangent spaceTangent spaceIn mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
at any point on a quaternion Slerp curve, the inverse of the exponential mapExponential mapIn differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
transforms the curve into a line segment. Slerp curves not extending through a point fail to transform into lines in that point's tangent space.
Quaternion Slerps are commonly used to construct smooth animation curves by mimicking affine constructions like the de Casteljau algorithmDe Casteljau's algorithmIn the mathematical field of numerical analysis, De Casteljau's algorithm is a recursive method to evaluate polynomials in Bernstein form or Bézier curves, named after its inventor Paul de Casteljau...
for Bézier curveBézier curveA Bézier curve is a parametric curve frequently used in computer graphics and related fields. Generalizations of Bézier curves to higher dimensions are called Bézier surfaces, of which the Bézier triangle is a special case....
s. Since the sphere is not an affine spaceAffine spaceIn mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
, familiar properties of affine constructions may fail, though the constructed curves may otherwise be entirely satisfactory. For example, the de Casteljau algorithm may be used to split a curve in affine space; this does not work on a sphere.
The two-valued Slerp can be extendedGeneralized quaternion interpolationGeneralized quaternion interpolation is an interpolation method that extends the quaternion slerp algorithm. This generalized method can interpolate between more than two unit-quaternions, but is neither closed-form nor fixed-time....
to interpolate among many unit quaternions, but the extension loses the fixed execution-timeTime complexityIn computer science, the time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the size of the input to the problem. The time complexity of an algorithm is commonly expressed using big O notation, which suppresses multiplicative constants and...
of the Slerp algorithm.
External links
- Ken Shoemake. Animating rotation with quaternion curves.
- Erik B. Dam, Martin Koch, Martin Lillholm. Quaternions, Interpolation and Animation.
- Understanding Slerp, Then Not Using It
- Brian Martin on quaternion animation